Содержание
- 2. Постановка задачи Корректирующий циклический (n, k) код представляется в полиномиальном виде как где F2[x] - кольцо
- 3. Корневой подход
- 4. Пример Обозначим примитивный элемент конечного поля GF(2m) как α. Определим проверочную матрицу H кода C ,
- 5. Пример
- 6. Корневой подход
- 7. Алгоритм формирования кода 1. Строится поле GF(pm) , для которого α - примитивный элемент поля. 2.
- 8. Теорема Пусть циклический код C длины n задан порождающим полиномом g(x) над полем GF(p) и пусть
- 9. Определение БЧХ Зададим циклический код C длины n над полем GF(p), определив наименьшее целое m такое,
- 10. БЧХ Если b = 1 то говорят, что код БЧХ определен в узком смысле. Если же
- 11. Соотношение между параметрами кода Для p = 2, b = 1, n = 2m – 1
- 12. Проверочная матрица БЧХ aj – элементы поля. Определитель ≠0, если aj – различны.
- 13. Galois Field GF(23) с неприводимым полиномом: x3 + x + 1 α = x примитивный элемент
- 14. GF Discrete Fourier Transform (DFT) GF-DFT Интерполяция полинома в n точках через умножение на матрицу: α
- 15. Вычисление минимальных полиномов через циклотомические классы
- 16. Сопряженные элементы Так для поля ??(16)=??(2^? ) минимальным многочленом элементов является один и тот же многочлен
- 17. Сопряженные элементы
- 18. Циклотомические классы
- 19. Циклотомические классы
- 20. Циклотомический класс
- 21. Пример
- 22. Минимальные полиномы Циклотомические классы позволяют вычислить минимальные полиномы с помощью выражения
- 23. Пример : исправление 1 ошибки Построим порождающий полином g(z) БЧХ-кода длины n = 23 – 1
- 24. GF(23) Мл.разряд
- 25. Пример: исправление 1 ошибки 3. Минимальный полином элемента α имеет вид m1(x) = (x + α)
- 26. Пример: исправление 2 ошибок Изменим условия примера, потребовав исправления до двух ошибок (t = 2 ⇒
- 27. Пример: исправление 2 ошибок Степень последнего равна трем, так что степень g(x) окажется равной шести, и
- 28. Построение БЧХ кода, корректирующего три ошибки Определим конечное поле GF(24), для которого существует четыре циклотомических класса
- 29. GF(24) Мл. разряд
- 30. Построение БЧХ кода, корректирующего три ошибки Элемент α3 является корнем полинома (x5 – 1). Элементы α
- 32. Скачать презентацию





























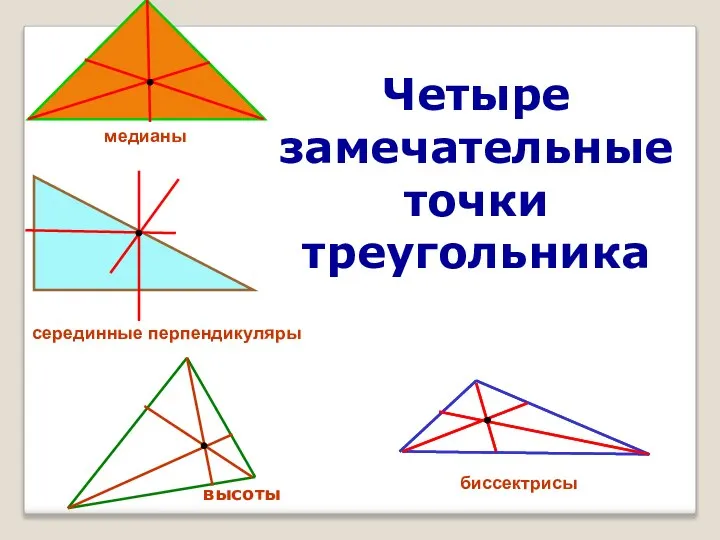 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Построение сечения плоскостью
Построение сечения плоскостью Площади многоугольников
Площади многоугольников Шкала. Координатный луч
Шкала. Координатный луч Измерение углов
Измерение углов Корреляционный и статистический анализ экспериментальных данных в программе Excel
Корреляционный и статистический анализ экспериментальных данных в программе Excel Коллекция картинок к урокам математики Часть 2
Коллекция картинок к урокам математики Часть 2 Теорема синусов Теорема косинусов Учитель математики Г.А.Ларькина Школа №91 г.Н.Новгород
Теорема синусов Теорема косинусов Учитель математики Г.А.Ларькина Школа №91 г.Н.Новгород  Коэффициент корреляции и корреляционный анализ
Коэффициент корреляции и корреляционный анализ 5 класс
5 класс  Соотношения между элементами прямоугольного треугольника
Соотношения между элементами прямоугольного треугольника Событие, вероятность события. Сложение и умножение вероятностей
Событие, вероятность события. Сложение и умножение вероятностей Системы линейных уравнений с двумя переменными
Системы линейных уравнений с двумя переменными Урок 11 Расстояния между прямыми
Урок 11 Расстояния между прямыми  Моделирование систем
Моделирование систем Открытый интенсив по математике. Как мощно подготовиться к экзамену? Ценность времени. День 2
Открытый интенсив по математике. Как мощно подготовиться к экзамену? Ценность времени. День 2 Исследование алфавита знаков для кодирования информации
Исследование алфавита знаков для кодирования информации Понятие вектора
Понятие вектора Повторительно-обобщающий урок по теме: «Показательная функция». 11 класс
Повторительно-обобщающий урок по теме: «Показательная функция». 11 класс Решение задач по теме "Векторы"
Решение задач по теме "Векторы" Сучасні методи моделювання в наукових дослідженнях
Сучасні методи моделювання в наукових дослідженнях Угол между прямыми. Подготовка к ЕГЭ С2
Угол между прямыми. Подготовка к ЕГЭ С2 Существование треугольника, равного данному
Существование треугольника, равного данному Пишите грамотно решение неполных квадратных уравнений
Пишите грамотно решение неполных квадратных уравнений Преобразование алгебраических выражений
Преобразование алгебраических выражений Презентация по математике Проценты
Презентация по математике Проценты  Оптимизация деятельности авторемонтного предприятия с помощью теории массового обслуживания
Оптимизация деятельности авторемонтного предприятия с помощью теории массового обслуживания Конус. Высота конуса
Конус. Высота конуса