Содержание
- 2. Введение Постиндустриальное общество, в котором мы живем, постепенно преобразуется в информационное. Напомню, что информационное общество –
- 3. ДЖОРДЖ БУЛЬ (1815 – 1864) Создателем алгебры логики является живший в ХIХ веке английский математик Джордж
- 4. Булевой алгеброй Алгеброй Буля называется непустое множество A с двумя бинарными операциями (конъюнкция, И), (дизъюнкция, ИЛИ),
- 5. Булевой функцией f(x1, x2, ... , xn) называется произвольная функция n переменных, аргументы которой x1, x2,
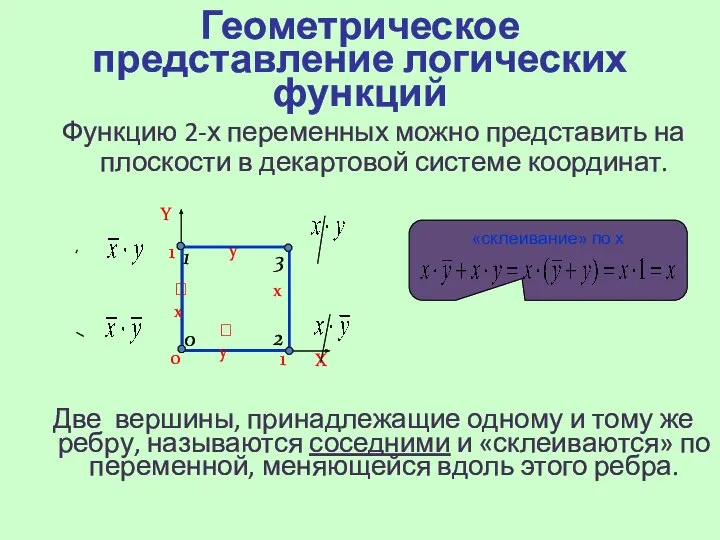
- 6. Геометрическое представление логических функций Функцию 2-х переменных можно представить на плоскости в декартовой системе координат. Две
- 7. Геометрическое представление логических функций Функцию 3-х переменных можно представить в 3-мерном пространстве декартовой системы координат в
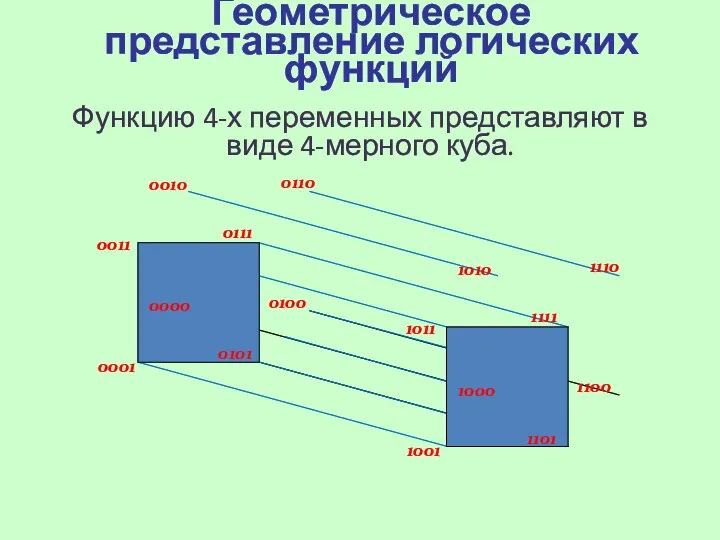
- 8. Геометрическое представление логических функций Функцию 4-х переменных представляют в виде 4-мерного куба.
- 9. Практически все булевы функции малых арностей (0, 1, 2 и 3) сложились исторически и имеют конкретные
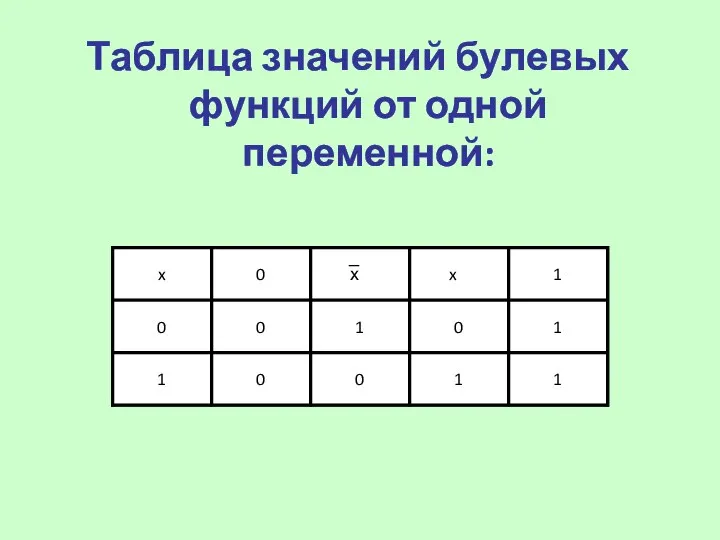
- 10. Таблица значений булевых функций от одной переменной:
- 11. Названия булевых функций от одной переменной:
- 12. Легко, не правда ли? Даже человек, который первый раз видит материал, составит таблицу за минуту, как
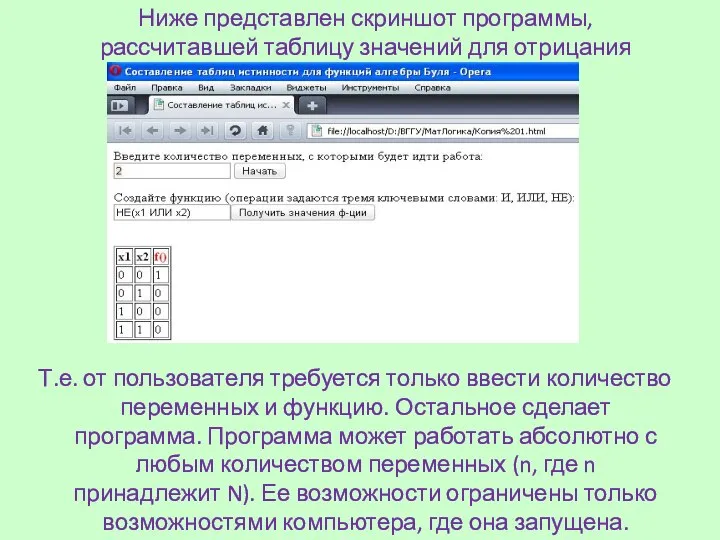
- 13. Ниже представлен скриншот программы, рассчитавшей таблицу значений для отрицания дизъюнкции Т.е. от пользователя требуется только ввести
- 14. Чуть выше мы рассмотрели само понятие булевой функции от n переменных. А сколько всего может быть
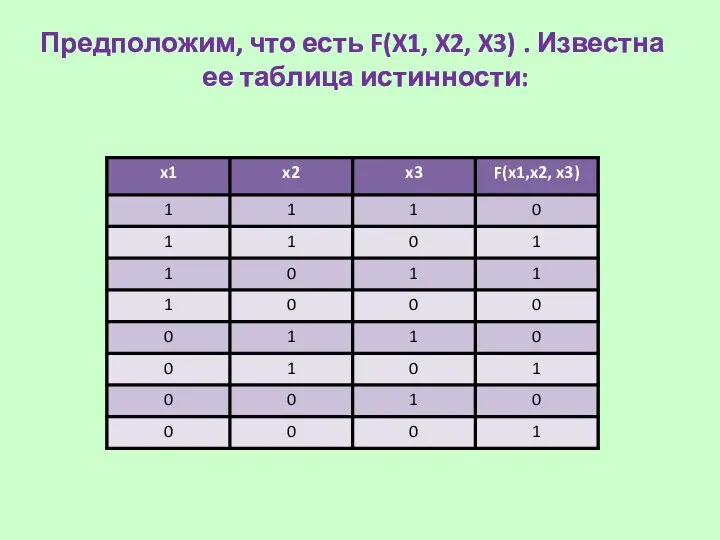
- 15. Предположим, что есть F(X1, X2, X3) . Известна ее таблица истинности:
- 17. Скачать презентацию









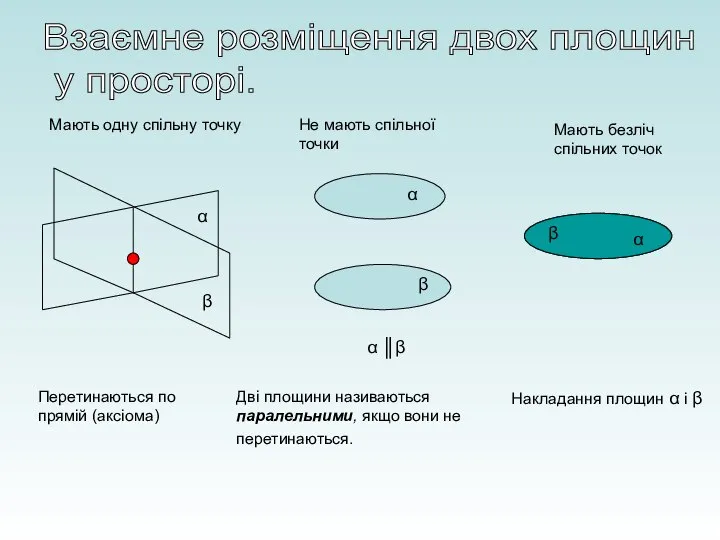 Паралельність площин
Паралельність площин Поверхности второго порядка
Поверхности второго порядка Схема Бернулли
Схема Бернулли Обобщающий урок геометрии за курс 8 класса
Обобщающий урок геометрии за курс 8 класса Тригонометрические формулы
Тригонометрические формулы Равнобокая трапеция из бумаги. Работа ножницами
Равнобокая трапеция из бумаги. Работа ножницами Площадь. Единицы измерения площади
Площадь. Единицы измерения площади Пространственные фигуры. Площадь, объем
Пространственные фигуры. Площадь, объем Презентация на тему Логарифмы и их свойства
Презентация на тему Логарифмы и их свойства  Вписанная и описанная пирамиды. Домашнее задание
Вписанная и описанная пирамиды. Домашнее задание Сложение и вычитание обыкновенных дробей
Сложение и вычитание обыкновенных дробей Прямоугольный параллелепипед. Урок обобщения и систематизации знаний
Прямоугольный параллелепипед. Урок обобщения и систематизации знаний Игра на поиск логических пар
Игра на поиск логических пар Практика по темам «Последовательность» и «Арифметическая прогрессия»
Практика по темам «Последовательность» и «Арифметическая прогрессия» Аттестационная работа. Образовательная программа внеурочной деятельности обучающихся Наглядная геометрия в 5-6 классах
Аттестационная работа. Образовательная программа внеурочной деятельности обучающихся Наглядная геометрия в 5-6 классах Теорема Пифагора
Теорема Пифагора Теорема Виета. Зависимость между корнями уравнения и его коэффициентами
Теорема Виета. Зависимость между корнями уравнения и его коэффициентами Площади фигур. Международная терминология
Площади фигур. Международная терминология Фалес из Милета. Теорема Фалеса
Фалес из Милета. Теорема Фалеса Үшбұрыштар теңдігінің белгілері
Үшбұрыштар теңдігінің белгілері Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Сумма и разность кубов двух выражений
Сумма и разность кубов двух выражений Деление десятичных дробей
Деление десятичных дробей Соотношения между единицами измерения величин. Единицы площади
Соотношения между единицами измерения величин. Единицы площади Разработка структуры следящего модуля фазовой автоподстройки частоты радиотехнических систем
Разработка структуры следящего модуля фазовой автоподстройки частоты радиотехнических систем Гамильтоновы циклы
Гамильтоновы циклы Алгебраические выражения
Алгебраические выражения История развития геометрии
История развития геометрии