Содержание
- 2. Характеризация равновесия по Нэшу ⊐ G = {I ; S ; U}, s∗ ∈ S ;
- 3. Квазивогнутые функции (quasiconcave) ⊐ F: ℝm → ℝ1. F – квазивогнутая функция, если для ∀ a
- 4. Теорема (достаточные условия существования равновесия по Нэшу) ⊐ G = {I ; S ; U}; для
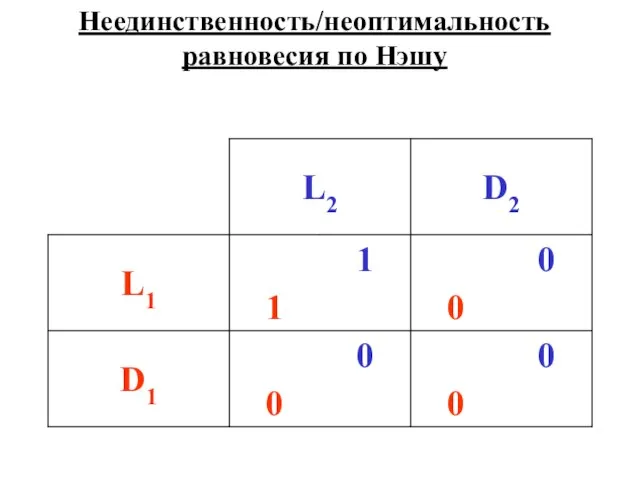
- 5. Неединственность/неоптимальность равновесия по Нэшу
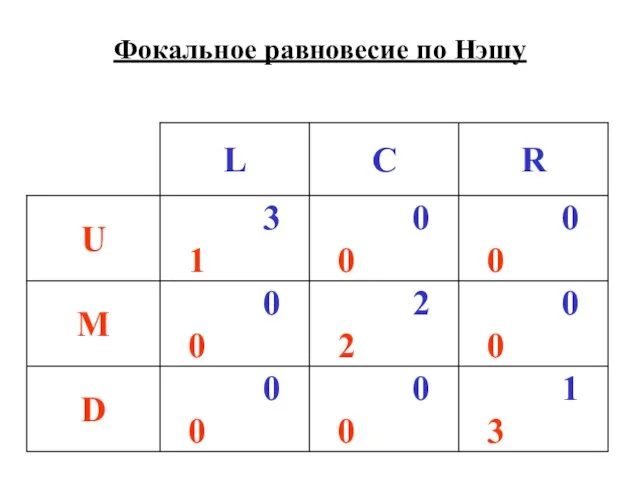
- 6. Фокальное равновесие по Нэшу
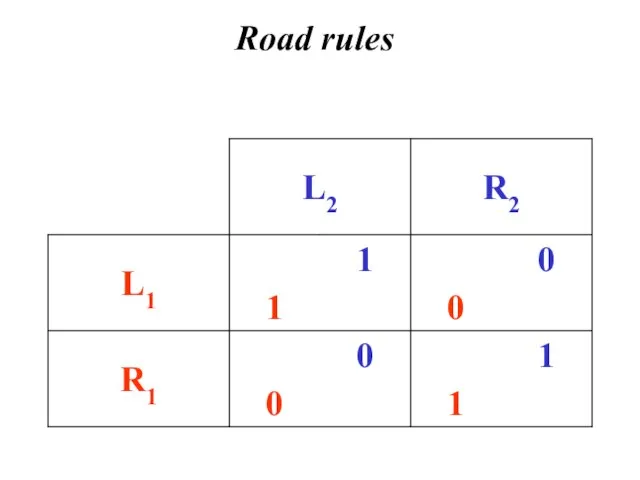
- 7. Road rules
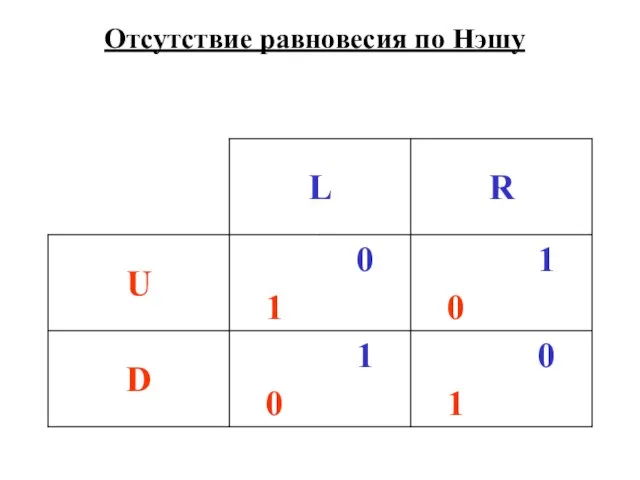
- 8. Отсутствие равновесия по Нэшу
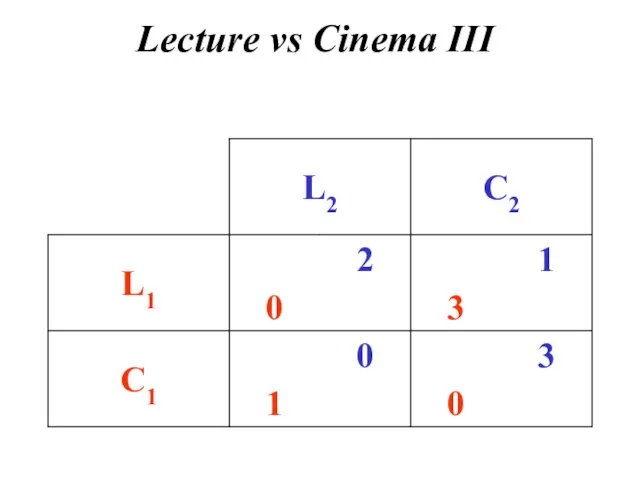
- 9. Lecture vs Cinema III
- 10. Симплексы ⊐ m ∈ ℕ. Симплекс размерности m – 1 есть S (m – 1) =
- 11. Чистые и смешанные стратегии (pure and mixed strategies) ⊐ G = {I ; S ; U},
- 12. Множества и профили смешанных стратегий ⊐ G = {I ; S ; U}, для ∀ i
- 13. Выигрыши по наборам смешанных стратегий ⊐ σ = (σ1, σ2, …, σn) – профиль смешанных стратегий
- 14. Смешанное расширение конечной игры (mixed expansion) ⊐ G = {I ; S ; U} – конечная
- 15. Носитель смешанной стратегии (mixed strategy support) ⊐ G = {I ; S ; U} – конечная
- 16. Полностью смешанные стратегии (completely mixed strategies) ⊐ G = {I ; S ; U} – конечная
- 17. Равновесие по Нэшу в смешанных стратегиях (mixed Nash equilibrium) ⊐ G = {I ; S ;
- 19. Скачать презентацию











 Нумерации разных народов и их возникновение
Нумерации разных народов и их возникновение  Математический тест для дошколят
Математический тест для дошколят Решение квадратных уравнений
Решение квадратных уравнений Распределения статистик (выборочные распределения)
Распределения статистик (выборочные распределения) Системы тригонометрических уравнений
Системы тригонометрических уравнений Дискретная математика. Лекция 1. Множества
Дискретная математика. Лекция 1. Множества Тригонометрия. (Лекция 2)
Тригонометрия. (Лекция 2) Неравенства с двумя переменными и их системы
Неравенства с двумя переменными и их системы Моделирование марковских случайных процессов
Моделирование марковских случайных процессов Аттестационная работа. 8 - 9 классы. Это удивительное понятие функция
Аттестационная работа. 8 - 9 классы. Это удивительное понятие функция Тригонометрический круг
Тригонометрический круг Решение задач с помощью уравнений
Решение задач с помощью уравнений Электронный учебник по алгебре для 7 класса
Электронный учебник по алгебре для 7 класса Квадратные корни. Их свойства
Квадратные корни. Их свойства Электронные методические материалы на тему: Золотое сечение для учащихся 5-6 классов
Электронные методические материалы на тему: Золотое сечение для учащихся 5-6 классов Спрощення ірраціональних виразів. Підготовка до ЗНО
Спрощення ірраціональних виразів. Підготовка до ЗНО Программа курса по высшей математике
Программа курса по высшей математике Урок геометрии в 7 классе «Искусство рассуждать»
Урок геометрии в 7 классе «Искусство рассуждать» Подготовка к ГИА по математике
Подготовка к ГИА по математике Тест по теме: "Тетраэдр и параллелепипед". Теория
Тест по теме: "Тетраэдр и параллелепипед". Теория Подготовка к контрольной работе
Подготовка к контрольной работе Презентация на тему Вычисление с многозначными числами
Презентация на тему Вычисление с многозначными числами  Метод рационализации при решении неравенств. Урок повторения по алгебре в 11 профильном классе
Метод рационализации при решении неравенств. Урок повторения по алгебре в 11 профильном классе Смежные углы
Смежные углы Презентация по математике "Сравнение обыкновенных и десятичных дробей" -
Презентация по математике "Сравнение обыкновенных и десятичных дробей" -  ДПА 11 класс Первообразная и интеграл
ДПА 11 класс Первообразная и интеграл Квадрат. Удивительные свойства квадрата Шарапова Мария, 6 класс МОУ СОШ № 37
Квадрат. Удивительные свойства квадрата Шарапова Мария, 6 класс МОУ СОШ № 37  Уравнения фигур
Уравнения фигур