Содержание
- 2. Производная функции Определение. Производной функции y = f (x) в точке x называется предел отношения приращения
- 3. Связь дифференцируемости и непрерывности функции Если функция дифференцируема в данной точке, то она непрерывна в ней.
- 4. Пусть f (x) и g (x) − дифференцируемые функции и с − константа, тогда справедливы соотношения
- 5. Теорема. (Производная сложной функции) Пусть функция g (x) имеет производную в точке x0, функция f (g)
- 6. Таблица производных
- 8. Пример Найти производные первого порядка функций Решение. Применим формулу производной суммы Далее используем формулы:
- 9. Тогда:
- 10. Решение. Используем правило дифференцирования произведения Далее, по таблице производных имеем: Формула (5): Формула (10):
- 12. Производная сложной функции. Вычислить производную Решение. Используем формулу В данном случае Тогда:
- 13. Теорема. (Производная функции, заданной параметрически) Если функция аргумента x задана параметрически: , α ≤ t ≤
- 14. Пусть функция у = f (x) задана уравнением F (x, y) = 0, не разрешенным относительно
- 15. Дифференциал функции Пусть функция имеет в точке x производную Тогда где при
- 16. Причем, Слагаемое - главная часть приращения функции.
- 17. Определение. Дифференциалом функции в точке называется главная часть приращения функции, равная произведению производной функции на приращение
- 20. Правило Лопиталя
- 22. Монотонность и экстремум функций
- 27. Производная от функции в точке равна угловому коэффициенту касательной к графику функции в точке с абсциссой
- 28. Уравнения касательной и нормали Уравнение касательной можно найти, используя уравнение прямой, проходящей через данную точку в
- 29. Уравнение нормали Прямая перпендикулярная касательной в точке касания называется нормалью к кривой. Угловые коэффициенты касательной и
- 30. Потому уравнение нормали в точке имеет вид: Углом между кривыми называют угол между касательными к кривым
- 31. Односторонние производные Определение. Если функция y = f (x) определена в левосторонней (правосторонней) окрестности точки x0
- 32. Теорема. (Необходимое и достаточное условие существования производной в точке) Функция y = f (x) имеет производную
- 33. Экономический смысл производной. Эластичность Пусть функция u=u(t) выражает количество произведенной продукции u за время t. Необходимо
- 34. Средняя производительность труда за этот период времени: Определение. Производительностью труда в момент называется предельное значение средней
- 35. Определение. Эластичностью функции y=f(x) в точке x называется предел Эластичность функции показывает на сколько процентов изменится
- 36. Пусть D=D(p) – функция спроса (зависит от цены товара p). Тогда под эластичностью спроса понимается процентное
- 38. Скачать презентацию







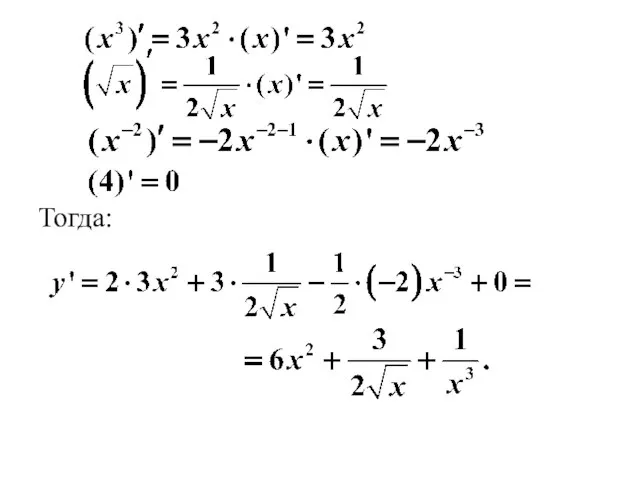



























 Розв’язування тригонометричних рівнянь
Розв’язування тригонометричних рівнянь Объём прямоугольного параллелепипеда
Объём прямоугольного параллелепипеда Невский проспект Санкт-Петербурга в цифрах. Станция метро "Площадь восстания" (часть 7)
Невский проспект Санкт-Петербурга в цифрах. Станция метро "Площадь восстания" (часть 7) Неравенство треугольника
Неравенство треугольника Матриці та дії над ними
Матриці та дії над ними Объемы шарового сегмента, шарового слоя и шарового сектора
Объемы шарового сегмента, шарового слоя и шарового сектора Сложение рациональных чисел 6 класс
Сложение рациональных чисел 6 класс Счастливый случай. 7 класс
Счастливый случай. 7 класс Корреляция. Причинность. Детерминизм
Корреляция. Причинность. Детерминизм Решение планиметрических задач на стереометрических чертежах
Решение планиметрических задач на стереометрических чертежах Действия с десятичными дробями 6 класс - Презентация_
Действия с десятичными дробями 6 класс - Презентация_ Понятие вероятности случайного события. Лекция №16
Понятие вероятности случайного события. Лекция №16 Единицы измерения площадей.
Единицы измерения площадей. Введение в эконометрику
Введение в эконометрику Организация вычислений с использованием относительных, абсолютных и смешанных ссылок
Организация вычислений с использованием относительных, абсолютных и смешанных ссылок Векторы и координаты
Векторы и координаты Математика 1 класс. Определение форм
Математика 1 класс. Определение форм Обслуговування заявок за пріоритетними дисциплінами
Обслуговування заявок за пріоритетними дисциплінами Тест по теме: "Признаки равенства треугольника"
Тест по теме: "Признаки равенства треугольника" Угол. Прямой и развернутый угол. Чертежный треугольник
Угол. Прямой и развернутый угол. Чертежный треугольник Числа от 10 до 20
Числа от 10 до 20 Алгоритм решения неравенств методом интервалов
Алгоритм решения неравенств методом интервалов Применение распределительного свойства умножения. 6 класс
Применение распределительного свойства умножения. 6 класс 5 класс
5 класс  Урок-экскурсия по Родному краю
Урок-экскурсия по Родному краю Десятичные дроби
Десятичные дроби Нахождение неизвестного числа в равенствах вида 12-х=7
Нахождение неизвестного числа в равенствах вида 12-х=7 Шкалирование информации
Шкалирование информации