Discrete random variables – expected variance and standard deviation. Discrete Probability Distributions. Week 7 (1)
Содержание
- 2. DR SUSANNE HANSEN SARAL
- 3. Cumulative Probability Function, F(x0) Practical application: Car dealer DR SUSANNE HANSEN SARAL The random variable, X,
- 4. Cumulative Probability Function, F(x0) Practical application DR SUSANNE HANSEN SARAL Example: If there are 3 cars
- 5. Cumulative Probability Function, F(x0) Practical application DR SUSANNE HANSEN SARAL Example: If only 2 cars are
- 6. Properties of discrete random variables: Expected value E[x] = (0 x .25) + (1 x .50)
- 7. Expected value for a discrete random variable Exercise X is a discrete random variable. The graph
- 8. Expected value for a discrete random variable X is a discrete random variable. The graph below
- 9. Expected variance of a Discrete Random Variables DR SUSANNE HANSEN SARAL
- 10. Variance of a discrete random variable DR SUSANNE HANSEN SARAL
- 11. Variance and Standard Deviation Ch. 4- DR SUSANNE HANSEN SARAL
- 12. At a car dealer the number of cars sold daily could vary between 0 and 5
- 13. Calculation of variance of discrete random variable. Car sales – example DR SUSANNE HANSEN SARAL
- 14. Class exercise A car dealer calculates the proportion of new cars sold that have been returned
- 15. Dan’s computer Works – class exercise The number of computers sold per day at Dan’s Computer
- 16. Dan’s computer Works – class exercise The number of computers sold per day at Dan’s Computer
- 17. Dan’s computer Works – class exercise The number of computers sold per day at Dan’s Computer
- 18. Dan’s computer Works – class exercise DR SUSANNE HANSEN SARAL
- 19. Quizz A small school employs 5 teachers who make between $40,000 and $70,000 per year. One
- 20. Khan Academy – Empirical Rule A company produces batteries with a mean life time of 1’300
- 21. Stating that two events are statistically independent means that the probability of one event occurring is
- 22. The time it takes a car to drive from Istanbul to Sinop is an example of
- 23. Probability is a numerical measure about the likelihood that an event will occur. TRUE FALSE
- 24. Suppose that you enter a lottery by obtaining one of 20 tickets that have been distributed.
- 25. If we flip a coin three times, the probability of getting three heads is 0.125. TRUE
- 26. The number of products bought at a local store is an example of a discrete random
- 27. Empirical rule – Khan Academy a) Which shape does a distribution need to have to apply
- 28. Probability Distributions Continuous Probability Distributions Binomial Probability Distributions Discrete Probability Distributions Uniform Normal Exponential DR SUSANNE
- 29. Binomial Probability Distribution Bi-nominal (from Latin) means: Two-names A fixed number of observations, n e.g., 15
- 30. Possible Binomial Distribution examples A manufacturing plant labels products as either defective or acceptable A firm
- 31. The Binomial Distribution The binomial distribution is used to find the probability of a specific or
- 32. The Binomial Distribution The binomial formula is: 2 – The symbol ! means factorial, and n!
- 33. Example: Calculating a Binomial Probability What is the probability of one success in five observations if
- 34. Binomial probability - Calculating binomial probabilities Suppose that Ali, a real estate agent, has 5 people
- 35. Solving Problems with the Binomial Formula Find the probability of 4 people buying a house out
- 36. Class exerise Find the probability of 3 people buying a house out of 5 people, when
- 37. P( X = 3) ? Find the probability of 3 people buying a house out of
- 38. Creating a probability distribution with the Binomial Formula – house sale example 2 – TABLE 2.8
- 39. Binomial Probability Distribution house sale example n = 5, P= .4 DR SUSANNE HANSEN SARAL
- 40. DR SUSANNE HANSEN SARAL
- 41. DR SUSANNE HANSEN SARAL
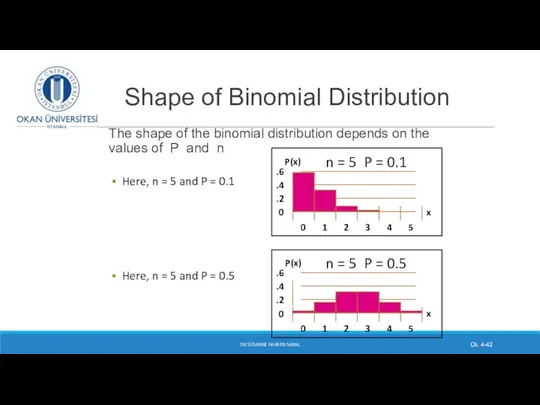
- 42. Shape of Binomial Distribution The shape of the binomial distribution depends on the values of P
- 43. Binomial Distribution shapes When P = .5 the shape of the distribution is perfectly symmetrical and
- 44. Using Binomial Tables instead of to calculating Binomial probabilites DR SUSANNE HANSEN SARAL Ch. 4- Examples:
- 45. Solving Problems with Binomial Tables MSA Electronics is experimenting with the manufacture of a new USB-stick
- 47. Скачать презентацию




![Properties of discrete random variables: Expected value E[x] = (0 x](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1465184/slide-5.jpg)





































 Математика. Решение задач
Математика. Решение задач Действия с натуральными числами. Урок-сказка
Действия с натуральными числами. Урок-сказка Производная сложной функции
Производная сложной функции Начертательная геометрия. Метод проекций
Начертательная геометрия. Метод проекций Математические ребусы. 6 класс
Математические ребусы. 6 класс Игра для 5 класса
Игра для 5 класса Действия с геометрическими фигурами, координатами и векторами
Действия с геометрическими фигурами, координатами и векторами Аксонометрическая проекция окружности
Аксонометрическая проекция окружности Структурные схемы и их преобразование. Типовые динамические звенья САУ и их классификация
Структурные схемы и их преобразование. Типовые динамические звенья САУ и их классификация Теория множеств. Понятие множества
Теория множеств. Понятие множества Заинька. Математическая раскраска. Реши примеры и покажи ответы
Заинька. Математическая раскраска. Реши примеры и покажи ответы Презентация по математике "Способы записи чисел" - скачать
Презентация по математике "Способы записи чисел" - скачать  Екі айнымалысы бар сызықтық теңдеудің графигі
Екі айнымалысы бар сызықтық теңдеудің графигі Векторы на плоскости
Векторы на плоскости Презентация по математике "Проценты. Начальные понятия" - скачать
Презентация по математике "Проценты. Начальные понятия" - скачать  Золотое сечение
Золотое сечение Свойства функций у = tgx и y = ctgx и их графики
Свойства функций у = tgx и y = ctgx и их графики 20160720_simmetriya
20160720_simmetriya Математика в поэзии
Математика в поэзии Деление с остатком
Деление с остатком Вписанная и описанная окружности
Вписанная и описанная окружности Обернена тригонометрична функція y=arcsinx
Обернена тригонометрична функція y=arcsinx Решение задач по теме «Площадь круга»
Решение задач по теме «Площадь круга» Графики квадратичных функций
Графики квадратичных функций Успешные люди – люди, которые в полной мере используют свой интеллект
Успешные люди – люди, которые в полной мере используют свой интеллект Применение первого признака равенства треугольников к решению задач
Применение первого признака равенства треугольников к решению задач «Своя игра». Внеклассное мероприятие по математике
«Своя игра». Внеклассное мероприятие по математике Автор: Галдин В. А. Учитель математики и физики МБОУ ЛСОШ №3 п. Локоть Брасовского р-на Электронная поста: galdin.vas@yandex.ru
Автор: Галдин В. А. Учитель математики и физики МБОУ ЛСОШ №3 п. Локоть Брасовского р-на Электронная поста: galdin.vas@yandex.ru