Содержание
- 2. Определение дискретной случайной величины Случайной называется величина, которая принимает в результате испытания то или иное (но
- 3. Определение закона распределения Законом распределения (рядом распределения) дискретной случайной величины называется соответствие, устанавливающее связь между возможными
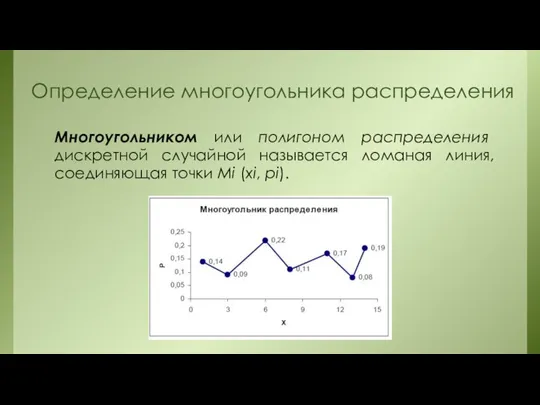
- 4. Определение многоугольника распределения Многоугольником или полигоном распределения дискретной случайной называется ломаная линия, соединяющая точки Mi (xi,
- 5. Определение функции распределения Функция распределения случайной величины F(x) определяет вероятность того, что случайная величина X примет
- 6. Построение функции распределения На основе закона распределения можно построить функцию распределения дискретной случайной величины Х.
- 7. Свойства функции распределения: Функция распределения F(x) – неубывающая, непрерывная слева функция, определенная на всей числовой оси,
- 8. Тема 1. Числові характеристики дискретної випадкової величини
- 9. Числовые характеристики дискретной случайной величины: Математическое ожидание Дисперсия Среднеквадратическое отклонение Мода
- 10. Математическое ожидание Математическое ожидание дискретной случайной величины равно сумме произведений значений случайной величины на их вероятности:
- 11. Дисперсия Дисперсией случайной величины X называется математическое ожидание квадрата ее отклонения от математического ожидания и равна
- 12. Среднее квадратическое отклонение Недостатком дисперсии является то, что ее размерность равна квадрату размерности случайной величины. Этого
- 13. Мода Модой (Мо) называется среднее значение случайной величины, которое встречается чаще всего, то есть имеет максимальную
- 14. Тема 2. Закони розподілу дискретної випадкової величини
- 15. Законы распределения дискретной случайной величины: Биномиальный Геометрический Гипергеометрический
- 16. Биномиальный закон распределения Пусть случайная величина X есть число появлений события A в n независимых испытаниях.
- 17. Закон распределения данной случайной величины X называется биномиальным законом, т.к. вероятности возможных ее значений равны элементам
- 18. Числовые характеристики биномиальной случайной величины математическое ожидание M (X ) = np , дисперсия D(X )
- 19. Геометрический закон распределения Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна
- 20. Геометрический закон распределения Закон распределения данной случайной величины X называется геометрическим законом. Геометрический закон может быть
- 21. Числовые характеристики геометрической случайной величины математическое ожидание дисперсия среднее квадратическое отклонение
- 22. Гипергеометрический закон распределения Пусть в корзине из N шаров имеется M белых (M Обозначим через Х
- 23. Гипергеометрический закон распределения Найдем число исходов, благоприятствующих событию X = m (среди взятых n шаров ровно
- 24. Гипергеометрический закон распределения Искомая вероятность равна отношению числа исходов, благоприятствующих событию X = m , к
- 25. Числовые характеристики гипергеометрической случайной величины математическое ожидание дисперсия среднее квадратическое отклонение
- 27. Скачать презентацию























 Презентация по математике "Прямоугольный треугольник. Задачи по готовым чертежам" - скачать бесплатно
Презентация по математике "Прямоугольный треугольник. Задачи по готовым чертежам" - скачать бесплатно Модели статистического прогнозирования (11класс)
Модели статистического прогнозирования (11класс) Поверхности. (Лекция 5)
Поверхности. (Лекция 5) Презентация по математике "Применение производной к исследованию функции" - скачать бесплатно
Презентация по математике "Применение производной к исследованию функции" - скачать бесплатно Числовые последовательности
Числовые последовательности Решение тестовых задач на движение (подготовка к ЕГЭ)
Решение тестовых задач на движение (подготовка к ЕГЭ) Объём шара и площадь сферы. Математический диктант
Объём шара и площадь сферы. Математический диктант Аксиомы в геометрии
Аксиомы в геометрии «Арифметика Магницкого»
«Арифметика Магницкого» Умножение и деление дробных чисел 6 класс МАОУ СОШ №10 г.Краснокамска Минина Т.А.
Умножение и деление дробных чисел 6 класс МАОУ СОШ №10 г.Краснокамска Минина Т.А.  Обобщающий урок по теме «Четырёхугольники.»
Обобщающий урок по теме «Четырёхугольники.» Геометрия
Геометрия Производная сложной функции
Производная сложной функции Кроссворд "Геометрические термины"
Кроссворд "Геометрические термины" Отображение Пуанкаре
Отображение Пуанкаре Нахождение высоты с помощью шеста
Нахождение высоты с помощью шеста Мультимедійна презентація проекту “Симетрія навколо нас“
Мультимедійна презентація проекту “Симетрія навколо нас“ Движения
Движения Объем шара и площадь сферы
Объем шара и площадь сферы Свойства проекции вектора на вектор. Линейные операции над векторами. (Лекция 4)
Свойства проекции вектора на вектор. Линейные операции над векторами. (Лекция 4) Линейные уравнения 1-го порядка. Уравнения Бернулли
Линейные уравнения 1-го порядка. Уравнения Бернулли Презентация по математике "Кто хочет стать математиком?" - скачать бесплатно
Презентация по математике "Кто хочет стать математиком?" - скачать бесплатно Правильні многогранники
Правильні многогранники Типы задач на проценты
Типы задач на проценты Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии
Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии Как люди научились считать
Как люди научились считать Равенство треугольников
Равенство треугольников Раскрытие скобок и заключение в скобки
Раскрытие скобок и заключение в скобки