Содержание
- 2. Введение Сети – это графы, которые моделируют реальные транспортные и коммуникационные сети.
- 3. Введение Задача о максимальном потоке в сети заключается в том, чтобы подсчитать максимальное количество некоторых объектов,
- 4. Введение Под объектами могут пониматься - пакеты данных, путешествующих по интернету; - коробки с товарами, которые
- 5. Введение Эта задача может использоваться при составлении расписания авиарейсов, распределения задач в суперкомпьютерах, обработке цифровых изображений
- 6. Введение Перемещение объектов могут ограничено пропускной способностью соединений сети или скоростью транспорта на загруженных дорогах.
- 7. Введение В задаче о максимальном потоке одна их вершин графа назначается истоком – точкой, в которой
- 8. Сети Сетью называется частично ориентированный граф G(V, E) Истоком и стоком (входным и выходным полюсом) называются
- 9. Сети Исток - вершина, локальная степень захода которой равна 0. Сток – вершина, локальная степень исхода
- 10. Сети Если в сети k истоков и m стоков – сеть называется (k,m)- полюсником. Если в
- 11. Сети Пусть s – исток, t – сток, так что любая другая вершина лежит на пути
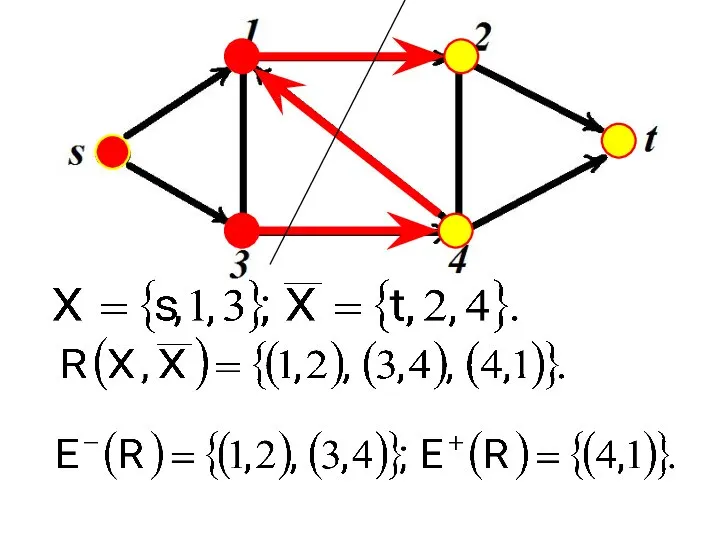
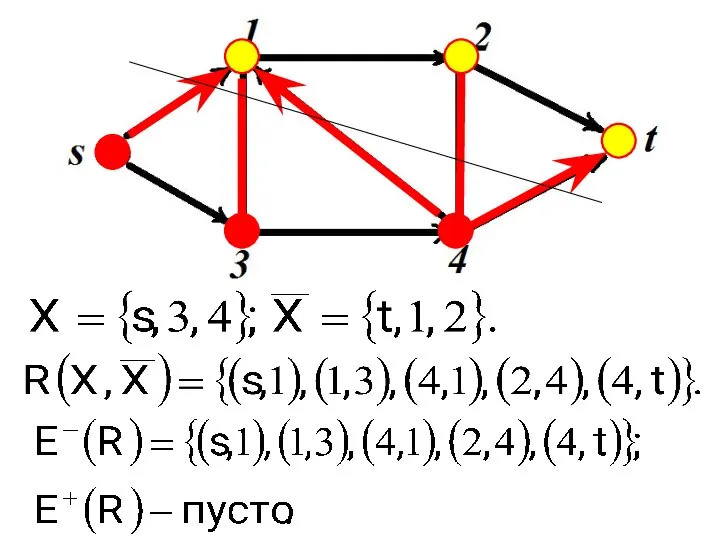
- 12. Сети Разобьем множество вершин V на два подмножества Х и таких, что , а . Множество
- 13. Сети Ориентированные ребра с началом в Х и концом в называются прямыми. Множество прямых ребер обозначим
- 14. Сети Ориентированные ребра с началом в и концом в Х называются обратными. Множество обратных ребер обозначим
- 15. Сети Все неориентированные ребра являются прямыми. Их ориентация произвольна, и определяется при задании потока в сети.
- 16. Сети Замечание 1: Прямым или обратным ребро будет в зависимости от вида разреза в сети.
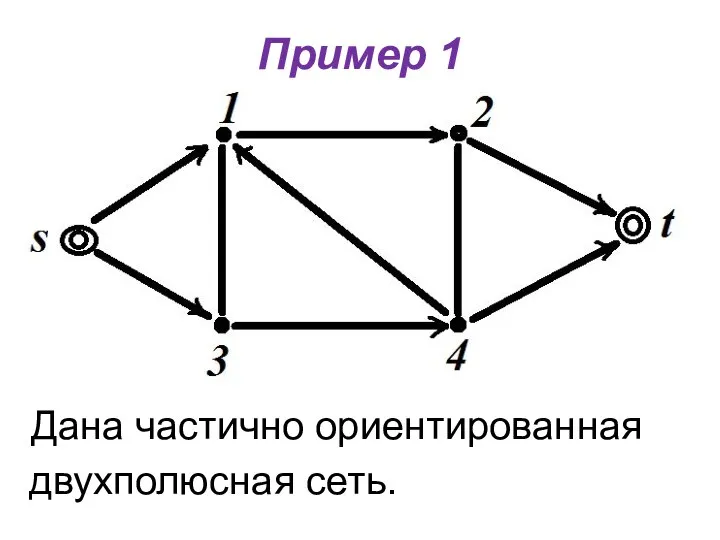
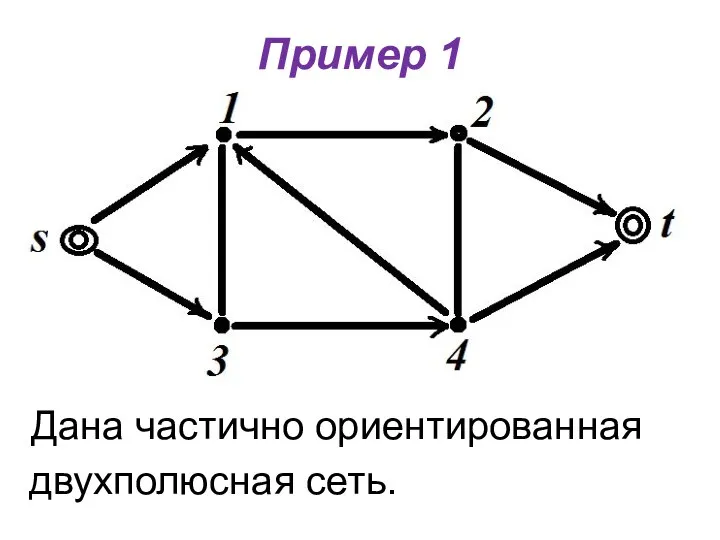
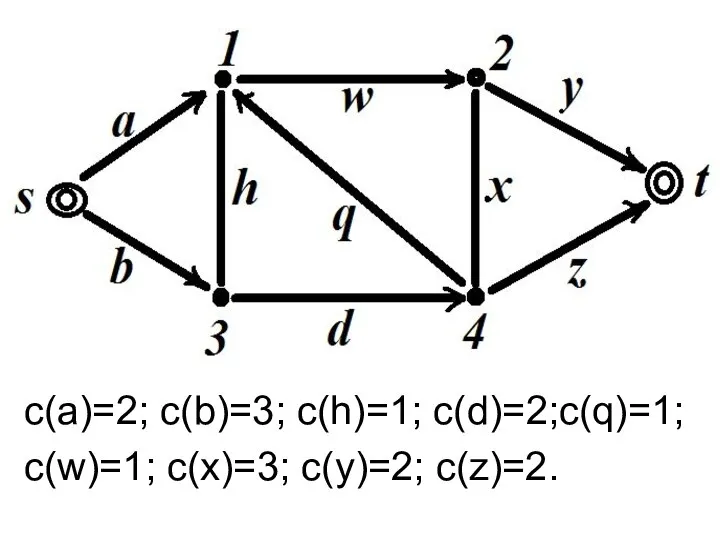
- 17. Пример 1 Дана частично ориентированная двухполюсная сеть.
- 22. Поток в сети Пусть S произвольная частично ориентированная сеть. Пусть каждому ребру сети приписано число пропускная
- 23. Поток в сети Потоком в сети S называется пара, составленная из числовой и нечисловой функций (f
- 24. Поток в сети Функция f удовлетворяет условиям: 1) 2) выполняется закон Киргофа: дивергенция любой внутренней вершины
- 25. Поток в сети Дивергенция вершины сети – число находимое по формуле:
- 26. Поток в сети Величина потока в сети S – равна дивергенции потока в вершине s (дивергенция
- 27. Поток в сети Замечание 2:
- 28. Поток в сети Замечание 3: Величина потока в сети есть величина переменная, зависящая от значений функции
- 29. Пример 1 Дана частично ориентированная двухполюсная сеть.
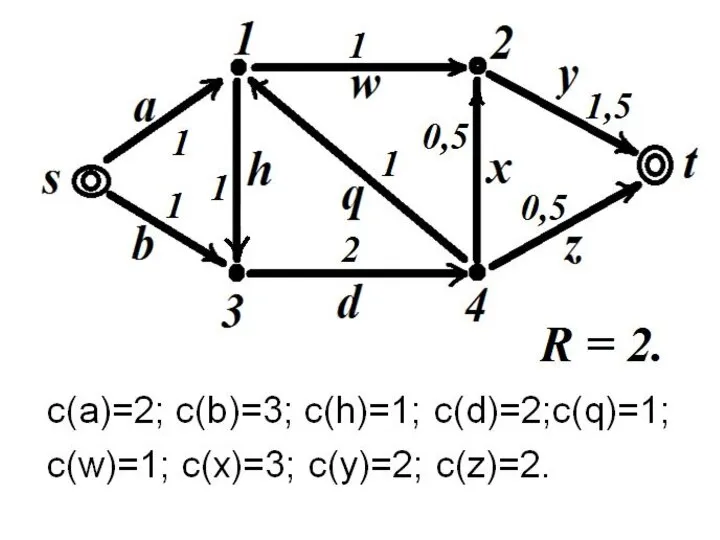
- 30. Поток в сети Замечание 3: Величина потока в сети есть величина переменная, зависящая от значений функции
- 31. с(a)=2; c(b)=3; c(h)=1; c(d)=2;c(q)=1; c(w)=1; c(x)=3; c(y)=2; c(z)=2.
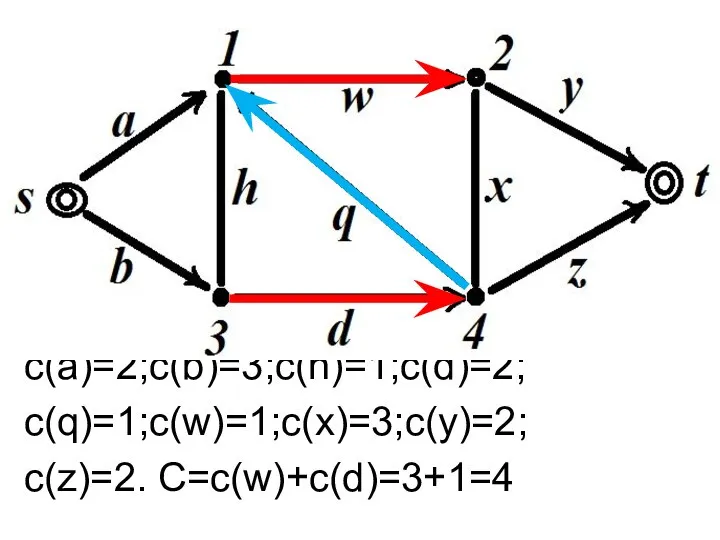
- 34. Поток в сети Каждому ребру разреза R ставится в соответствие пропускная способность разреза с(R), равная сумме
- 35. с(a)=2;c(b)=3;c(h)=1;c(d)=2; c(q)=1;c(w)=1;c(x)=3;c(y)=2; c(z)=2. C=c(w)+c(d)=3+1=4
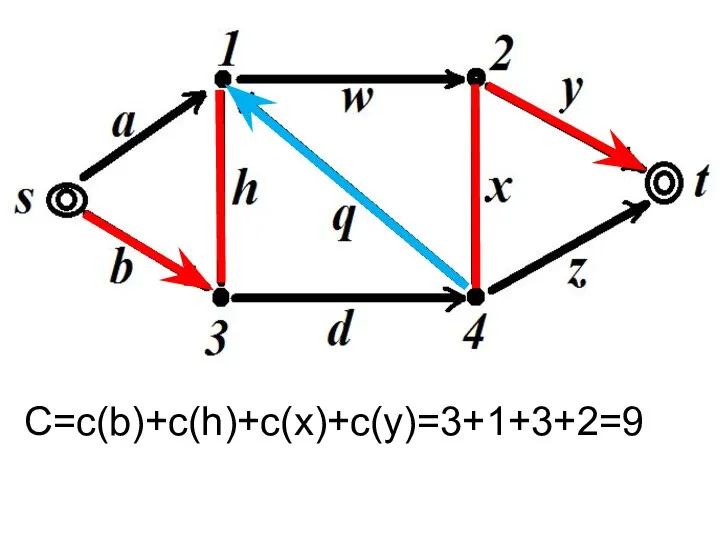
- 36. C=c(b)+c(h)+c(x)+c(y)=3+1+3+2=9
- 38. Скачать презентацию



























 Аттестационная работа. Работа с учащимися над проектом Математика в быту и повседневной жизни
Аттестационная работа. Работа с учащимися над проектом Математика в быту и повседневной жизни Урок веселой математики. (5 класс)
Урок веселой математики. (5 класс) Счет десятками до 100
Счет десятками до 100 Измерительные работы
Измерительные работы Математический КВН (5 класс)
Математический КВН (5 класс) Ранг матрицы. Собственные числа и собственные векторы
Ранг матрицы. Собственные числа и собственные векторы Действия с геометрическими фигурами
Действия с геометрическими фигурами Аттестационная работа. Исследовательская деятельность на уроках математики
Аттестационная работа. Исследовательская деятельность на уроках математики Уравнения n-ой степени
Уравнения n-ой степени Решение задач в два действия (1 класс)
Решение задач в два действия (1 класс) Формирование универсальных учебных действий при решении текстовых задач
Формирование универсальных учебных действий при решении текстовых задач Подобные слагаемые
Подобные слагаемые Сравнение десятичных дробей
Сравнение десятичных дробей Задачи на смеси, сплавы и растворы
Задачи на смеси, сплавы и растворы Комбинаторные задачи. Урок № 100
Комбинаторные задачи. Урок № 100 Производная и её применение
Производная и её применение Теорема косинусов для треугольника (задача)
Теорема косинусов для треугольника (задача) Урок – смотр знаний (с элементами игры ) Учитель Нестерова Ирина Владимировна МОУСОШ № 24
Урок – смотр знаний (с элементами игры ) Учитель Нестерова Ирина Владимировна МОУСОШ № 24 Замкнутая линия и многоугольник
Замкнутая линия и многоугольник Квадратные уравнения
Квадратные уравнения Перпендикулярные прямые
Перпендикулярные прямые Симплекс-метод
Симплекс-метод Л. Эйлер и развитие математического анализа в XVIII веке
Л. Эйлер и развитие математического анализа в XVIII веке Математические методы проектирования инфокоммуникационных систем. Предмет курса. Основные понятия
Математические методы проектирования инфокоммуникационных систем. Предмет курса. Основные понятия 1 признак подобия
1 признак подобия Подобные треугольники
Подобные треугольники Построение треугольника по трем элементам
Построение треугольника по трем элементам Равносильные уравнения и неравенства
Равносильные уравнения и неравенства