Содержание
- 2. Определения Эффективно перечислимым множеством называется множество, элементы которого можно перечислить по алгоритму (пронумеровать натуральным рядом без
- 3. Теорема Поста Если множество А эффективно перечислимо, то подмножество В эффективно распознается в А тогда и
- 4. Теорема Поста достаточность Пусть B и А\B эффективно перечислимы. Множества В и А\B представляет собой набор
- 5. Теорема Поста Для каждого элемента запустим параллельно алгоритмы перечисления В и А\В (поочерёдно по одному элементу
- 6. Теорема Множество машин Тьюринга эффективно перечислимо. Доказательство: Идея: описать произвольную машину Тьюринга некоторым числом, которое эффективно
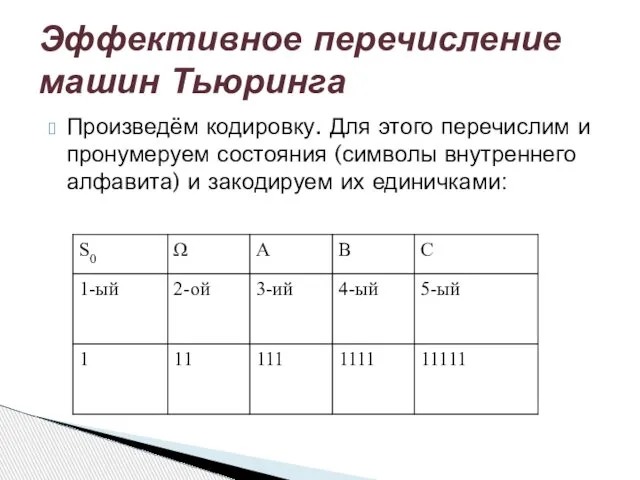
- 7. Произведём кодировку. Для этого перечислим и пронумеруем состояния (символы внутреннего алфавита) и закодируем их единичками: Эффективное
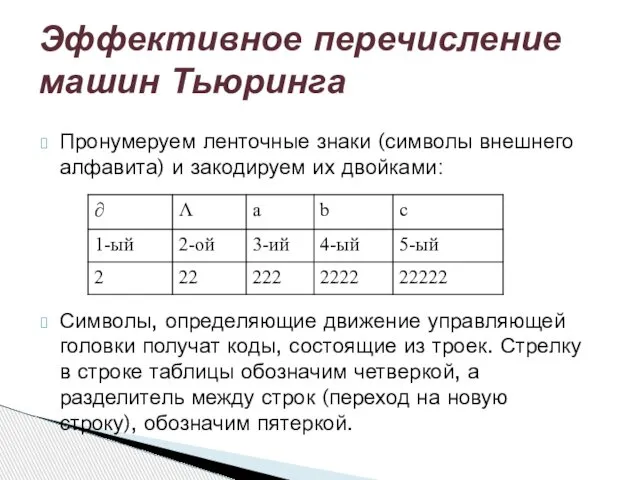
- 8. Пронумеруем ленточные знаки (символы внешнего алфавита) и закодируем их двойками: Символы, определяющие движение управляющей головки получат
- 9. Эффективное перечисление машин Тьюринга Например, А а ? b L B ?? 111222422223311115. Поменяем местами символы
- 10. Теперь можно убрать “4” и “5”, тогда получим 222111222233111, тем самым уменьшив длину кода (данный шаг
- 11. Теорема Множество алгоритмов Маркова эффективно перечислимо. Доказательство: Идея: описать произвольный алгоритм некоторым числом, которое эффективно распознаётся
- 12. Произведём кодировку: Нормальный алгоритм представляет собой набор строк, например: ab → c Λ ? d •
- 13. Если мы возьмем ряд простых чисел и каждое из них возведём в какую-нибудь степень, а затем
- 14. Возьмём первую строчку алгоритма Маркова и представим её следующим образом: a b → c 24 •
- 15. Далее формируем кодовое число всего алгоритма. Для этого выпишем ряд простых чисел и возведем каждое число
- 16. Теперь возьмем ряд натуральных чисел и применим к нему алгоритм распознавания, определяющий является ли данное число
- 17. Доказательство: Возьмем множество машин, останавливающихся на первом такте, и пронумеруем их: T11,T12,T13,T14… Затем пронумеруем множество машин,
- 18. Используя диагональный метод, перечислим их (пронумеруем натуральными числами): Таким образом, каждая останавливающаяся машина Тьюринга получит свой
- 19. Доказательство: Предположим противное, а именно, что множество не останавливающихся машин эффективно перечислимо. Тогда используем Теорему Поста,
- 21. Скачать презентацию
















 Плоские фигуры в нашей жизни
Плоские фигуры в нашей жизни Высоты треугольника
Высоты треугольника МОУ «Чалтырская средняя общеобразовательная школа №1» Мясниковского района Ростовской области Анания Ширакаци и его задачи Ра
МОУ «Чалтырская средняя общеобразовательная школа №1» Мясниковского района Ростовской области Анания Ширакаци и его задачи Ра Геометрический смысл производной. Определение
Геометрический смысл производной. Определение Геометрические иллюзии, или всегда ли мы видим то, что видим
Геометрические иллюзии, или всегда ли мы видим то, что видим Двоичная система счисления
Двоичная система счисления Правила сравнения чисел
Правила сравнения чисел Кері байланыс
Кері байланыс Перестановка слагаемых. Применение переместительного свойства
Перестановка слагаемых. Применение переместительного свойства Задача на арифметическую прогрессию (2)
Задача на арифметическую прогрессию (2) Измерение длины отрезка
Измерение длины отрезка Симметрия в пространстве
Симметрия в пространстве Планиметрия. Стереометрия
Планиметрия. Стереометрия Урок математики Устный счет
Урок математики Устный счет Крамер методы һәм Microsoft Excel программасы ярдәмендә сызыкча тигезләмәләр системасын чишү
Крамер методы һәм Microsoft Excel программасы ярдәмендә сызыкча тигезләмәләр системасын чишү Потребительский кредит Погашение основного долга равными выплатами Правило «78»
Потребительский кредит Погашение основного долга равными выплатами Правило «78» Математические задачи от русских, советских и зарубежных писателей
Математические задачи от русских, советских и зарубежных писателей Вероятностные умозаключения
Вероятностные умозаключения Аттестационная работа. Практико-ориентированные задачи на уроках математики
Аттестационная работа. Практико-ориентированные задачи на уроках математики Своя игра. 7 класс
Своя игра. 7 класс Окружность и её элементы
Окружность и её элементы Развёртка прямоугольного параллелепипеда. Урок 142
Развёртка прямоугольного параллелепипеда. Урок 142 Деление на трехзначное число
Деление на трехзначное число Ряд Фурье. Преобразование Фурье, его свойства. Дискретное преобразование Фурье. Быстрое преобразование Фурье. Лекция 8
Ряд Фурье. Преобразование Фурье, его свойства. Дискретное преобразование Фурье. Быстрое преобразование Фурье. Лекция 8 Математика 1 класс. Сложение с переходом через десяток
Математика 1 класс. Сложение с переходом через десяток Исследовательский проект Автор: Калиниченко Мария ученица 5в класса МОУ СОШ №5 г.
Исследовательский проект Автор: Калиниченко Мария ученица 5в класса МОУ СОШ №5 г. Арифметическая прогрессия вокруг нас
Арифметическая прогрессия вокруг нас Тест по теме: "Сумма углов треугольника"
Тест по теме: "Сумма углов треугольника"