Эконометрика. Лекция № 2. Парная (простая) регрессия

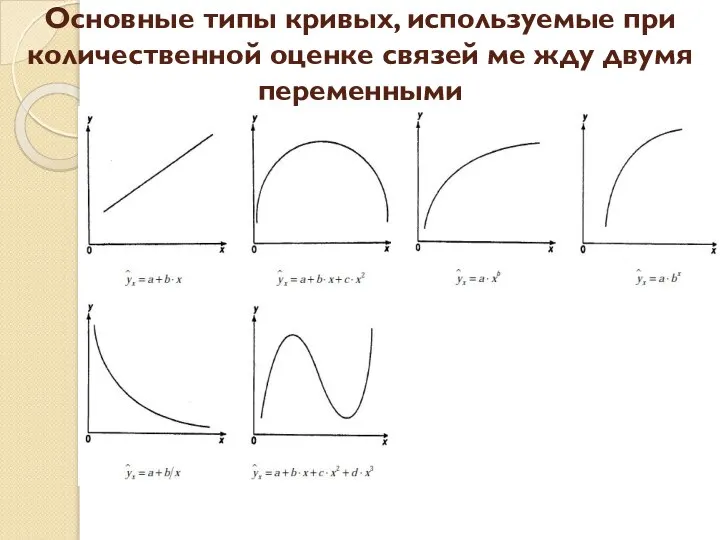
среднее значение зависимой (объясняемой) переменной рассматривается как функция одной независимой (объясняющей) переменной x , т.е. это модель вида:

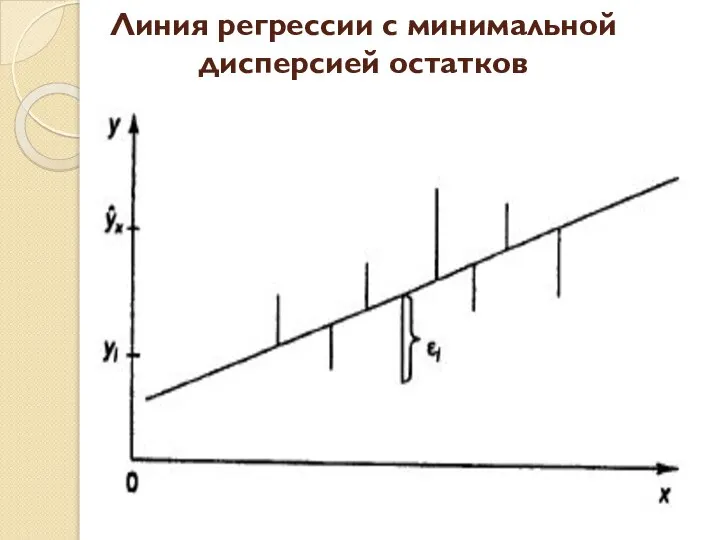
В каждом отдельном случае величина y складывается из двух слагаемых:

где y – фактическое значение результативного признака; – теоретическое значение результативного признака, найденное исходя из уравнения регрессии; ε – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.

измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.

Методы выбора вида математической функции:
1) графический;
2) аналитический, т.е. исходя из теории изучаемой взаимосвязи;
3) экспериментальный.

ожиданию произведения отклонений этих случайных величин от их математических ожиданий.
Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности.

Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

регрессией, в общей дисперсии результативного признака:

Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

регрессии в целом производится на основе F -критерия Фишера, которому предшествует дисперсионный анализ.

число параметров при переменной x ).

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F - критерия Фишера:

2 степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала.
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t -критерия Стьюдента:
которое затем сравнивается с табличным значением при определенном уровне значимости α и числе степеней свободы (n - 2). Доверительный интервал для коэффициента регрессии определяется как . Поскольку знак коэффициента регрессии указывает на рост результативного признака y при увеличении признака-фактора x (b > 0), уменьшение результативного признака при увеличении признака-фактора (b < 0) или его независимость от независимой переменной (b = 0), то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, -1,5 ≤ b ≤ 0,8. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.

внутренне линейные (приводятся к линейному виду с помощью
соответствующих преобразований, например, логарифмированием);
нелинейные модели внутренне нелинейные (к линейному виду не приводятся).

регрессии