Содержание
- 2. Восемь способов решения одного тригонометрического уравнения. 1.Приведение уравнения к однородному. 2.Разложение левой части уравнения на множители.
- 3. Задача. Решите уравнение различными способами. sin x – cos x = 1 ?
- 4. Способ первый. Приведение уравнения к однородному. Это однородное уравнение первой степени. Делим обе части этого уравнения
- 5. Способ второй. Разложение левой части уравнения на множители. Далее так, как в первом способе.
- 6. Способ третий. Введение вспомогательного угла. В левой части вынесем - корень квадратный из суммы квадратов коэффициентов
- 7. Внимание! Эквивалентны ли результаты , полученные в рассмотренных способах решений данного уравнения sin x – cosx
- 8. Способ четвертый. Преобразование разности (или суммы) тригонометрических функций в произведение. Запишем уравнение sin x – cosx
- 9. Способ пятый. Приведение к квадратному уравнению относительно одной функции. Возведем обе части уравнения в квадрат: или
- 10. Способ шестой. Возведение обеих частей уравнения в квадрат. sin x – cos x = 1 Ответ:
- 11. Способ седьмой. Универсальная подстановка . Выражение всех функций через (универсальная подстановка) по формулам: sin x –cosx
- 12. Внимание! Могли потерять корни.Необходима проверка! Область допустимых значений первоначального уравнения - всё множество R . При
- 14. Скачать презентацию











 Сложение чисел с разными знаками
Сложение чисел с разными знаками Яковлева Ксения ученица 11 класса МБОУ «СОШ№22» г. Анжеро-Судженск, Кемеровской области Научный руководитель: Лилия Геннадьевна
Яковлева Ксения ученица 11 класса МБОУ «СОШ№22» г. Анжеро-Судженск, Кемеровской области Научный руководитель: Лилия Геннадьевна Функциональная грамотность на уроках математики
Функциональная грамотность на уроках математики Начальные сведения по теории вероятностей
Начальные сведения по теории вероятностей Координаты вектора
Координаты вектора Презентация на тему Перестановка слагаемых
Презентация на тему Перестановка слагаемых Чертежи разверток поверхностей геометрических тел
Чертежи разверток поверхностей геометрических тел Ребусы по математике
Ребусы по математике Математика, 5 класс Автор - Логунова Л.В.
Математика, 5 класс Автор - Логунова Л.В.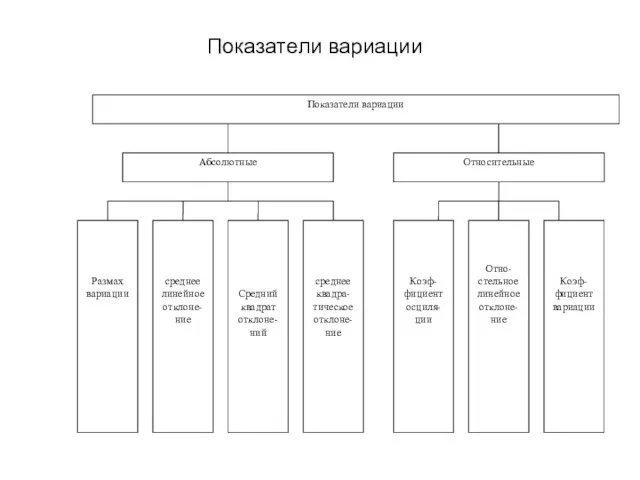 Показатели вариации
Показатели вариации пределы (1)
пределы (1) Эквивалентные отношения. Свойства эквивалентности
Эквивалентные отношения. Свойства эквивалентности Тренажер по графикам функций
Тренажер по графикам функций Случаи сложения и вычитания основанные на знаниях нумерации
Случаи сложения и вычитания основанные на знаниях нумерации Задачи на движение
Задачи на движение Начинаем мы опять решать, отгадывать, считать
Начинаем мы опять решать, отгадывать, считать Комбинаторика. Правило суммы
Комбинаторика. Правило суммы Построение таблиц истинности. Решение логических задач
Построение таблиц истинности. Решение логических задач Решение задач по математике
Решение задач по математике Solution methods for bilevel optimization
Solution methods for bilevel optimization Презентация к уроку алгебры Презентация к уроку алгебры в 10 классе по теме «Формулы суммы и разности синуса и косинуса.» Учит
Презентация к уроку алгебры Презентация к уроку алгебры в 10 классе по теме «Формулы суммы и разности синуса и косинуса.» Учит Умножение десятичной дроби на натуральное число
Умножение десятичной дроби на натуральное число Ломаные линии и многоугольники
Ломаные линии и многоугольники Устная работа (5m)2 (а4)3 57.63
Устная работа (5m)2 (а4)3 57.63  Выражения, тождества, уравнения
Выражения, тождества, уравнения Открытия Гаусса, Абеля и Галуа
Открытия Гаусса, Абеля и Галуа Презентация Учет инфляции в финансовых вычислениях
Презентация Учет инфляции в финансовых вычислениях Аттестационная работа. Исследовательская деятельность учащихся при построении доказательств по математике. (5-6 класс)
Аттестационная работа. Исследовательская деятельность учащихся при построении доказательств по математике. (5-6 класс)