Содержание
- 2. Исторические сведения Начиная лишь с 17 века, в связи с проникновением в математику идеи переменных, понятие
- 3. Постепенно понятие функции стало отождествляться, таким образом, с понятием аналитического выражения - формулы. В 1671 году
- 4. Великий математик - Дирихле Дирихле Петер Густав Лежён (13.02.1805 - 05.05.1859) Немецкий математик, иностранный чл.-корр. Петербургской
- 5. Дирихле доказал теорему о существовании бесконечно большого числа простых чисел во всякой арифметической прогрессии из целых
- 6. Что такое функция? Функция-это зависимость одной переменной от другой. Когда каждому значению одной переменной соответствует единственное
- 7. Различные способы задания функции Аналитический, графический, табличный – наиболее простые, а потому наиболее популярные способы задания
- 8. Аналитический способ Функция задана аналитически- это значит , указывается формула, позволяющая получить значение зависимой переменной, подставив
- 9. Табличный способ При табличном способе задания функции заполняется таблица, где в первой строчке указывается значение независимой
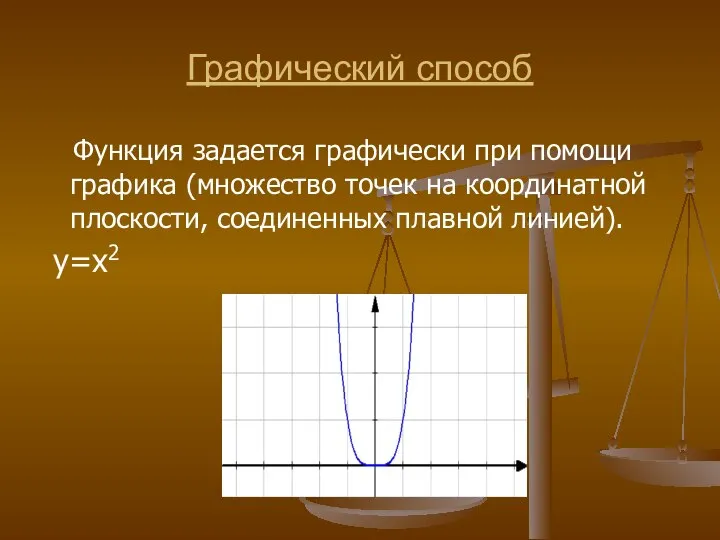
- 10. Графический способ Функция задается графически при помощи графика (множество точек на координатной плоскости, соединенных плавной линией).
- 11. Словесный способ задания функции Функция может быть задана и словесно, т. е. описательно. Например, так называемая
- 12. Из всех указанных способов задания функции наибольшие возможности для применения аппарата математического анализа дает аналитический способ,
- 13. Свойства функций Область значения функции Е(у) -множество значений переменной у, при которых функция существует или определена.
- 14. чётные и нечётные функции Область определения функции D (f) – симметричное 2. Для любого Х выполняется
- 15. Знакопостоянство функций. Промежутками знакопостоянства называются такие промежутки, на которых функция не меняет своего знака, т.е. принимает
- 16. Исследование функций на монотонность если двигаться по графику слева направо, то ординаты точек графика всё время
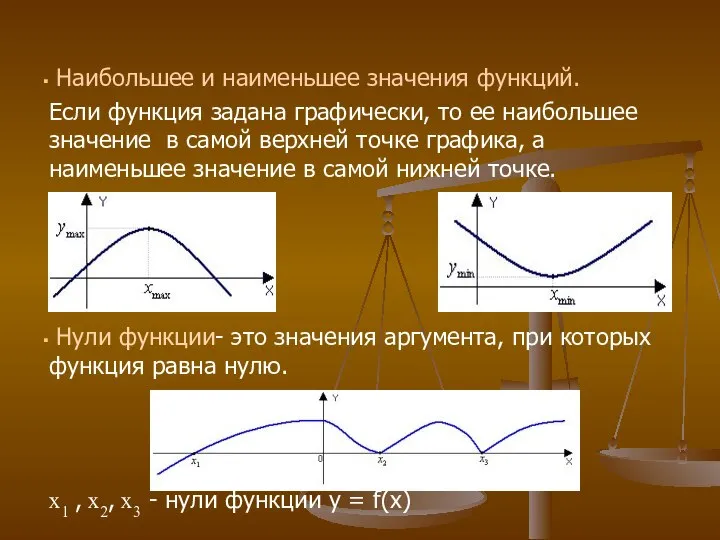
- 17. Наибольшее и наименьшее значения функций. Если функция задана графически, то ее наибольшее значение в самой верхней
- 18. Периодичность. Если функция задана графически, то она является периодической , если график повторяется через определенный интервал(период).
- 19. Ограниченность функции Функция у = f (x) называют ограниченной снизу на множестве Х ⊂ D (f),
- 20. х у 0 у = m m х у 0 у =M M Ограниченность функции у
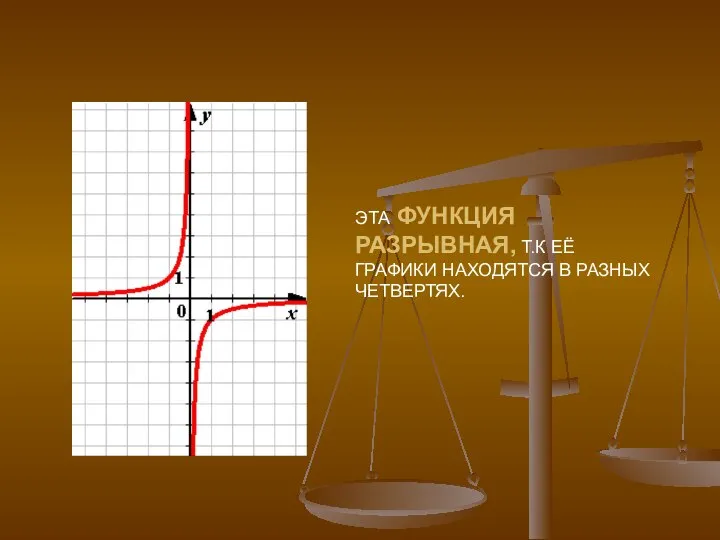
- 21. Непрерывность функции. Если функция задана графически , то она непрерывна, если ее график представляет собой непрерывную
- 22. ЭТА ФУНКЦИЯ РАЗРЫВНАЯ, Т.К ЕЁ ГРАФИКИ НАХОДЯТСЯ В РАЗНЫХ ЧЕТВЕРТЯХ.
- 23. Выпуклость функции х у 0 х у 0 Выпуклая функция — функция, у которой надграфик является
- 24. Ф ункции
- 25. График постоянной функции х у 0 у = k С
- 26. х у 0 k > 0 возрастающая х у 0 k убывающая Линейная функция у =
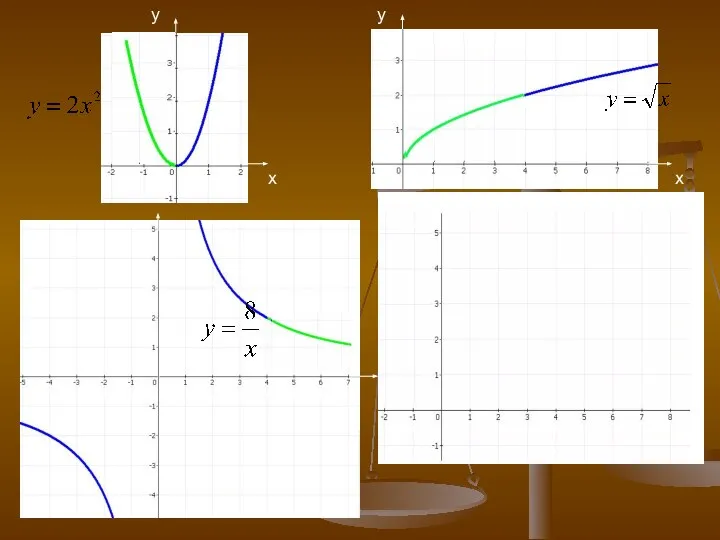
- 27. Функция у = kx2 1. D (f) = (-∞;+∞) k > 0 k x y 0
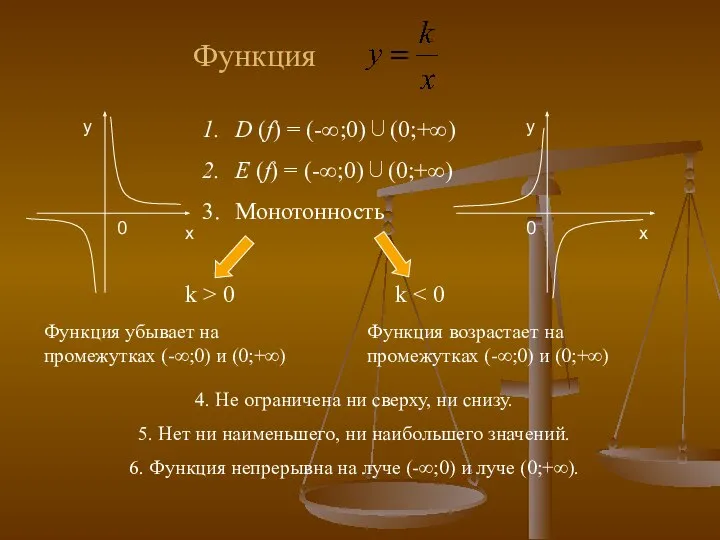
- 28. Функция D (f) = (-∞;0)∪(0;+∞) Е (f) = (-∞;0)∪(0;+∞) Монотонность k > 0 k Функция убывает
- 29. Доказательство : 1. Пусть у = f (x), где f (x) = kx + m. 1)
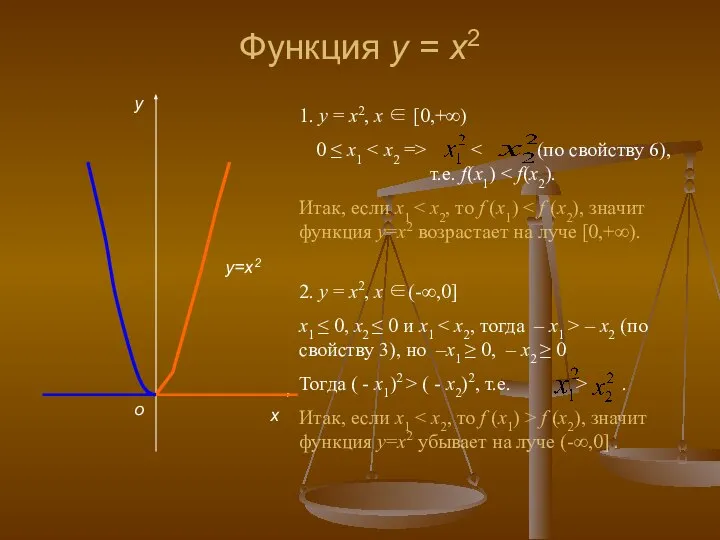
- 30. Функция у = х2 х о у у=х2 1. у = х2, х ∈ [0,+∞) 0
- 31. Функция х о у Пусть у = f (x), где , x ∈(0,+∞) 0 > ,
- 32. Кубическая парабола График функции y = х 3 (кубическая парабола) Построим график функции y = х
- 33. D (f) = [ - 3; 6] E (f) = [1; 2] Постоянна на [ -
- 34. Построить график функции
- 35. х у у х х у у у х
- 36. ① ② ③ ④ ⑤ ⑥ ⑦ Степенная функция и её график p=2n p=2n-1 P>1 p=-(2n-1)
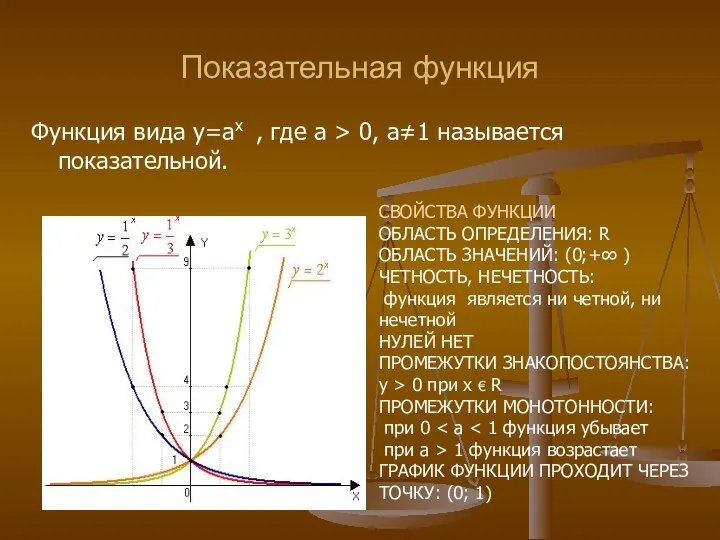
- 37. Показательная функция Функция вида y=ax , где a > 0, a≠1 называется показательной. СВОЙСТВА ФУНКЦИИ ОБЛАСТЬ
- 38. Свойства показательной функции Показательная функция существует при любом значении аргумента Может принимать только положительные значения Функция
- 39. Логарифмическая функция Функция вида y=log x a, где a > 0, a≠1 называется логарифмической. Свойства функции
- 40. Свойства логарифмической функции Логарифмическая функция существует только при положительных значениях аргумента Сама логарифмическая функция может принимать
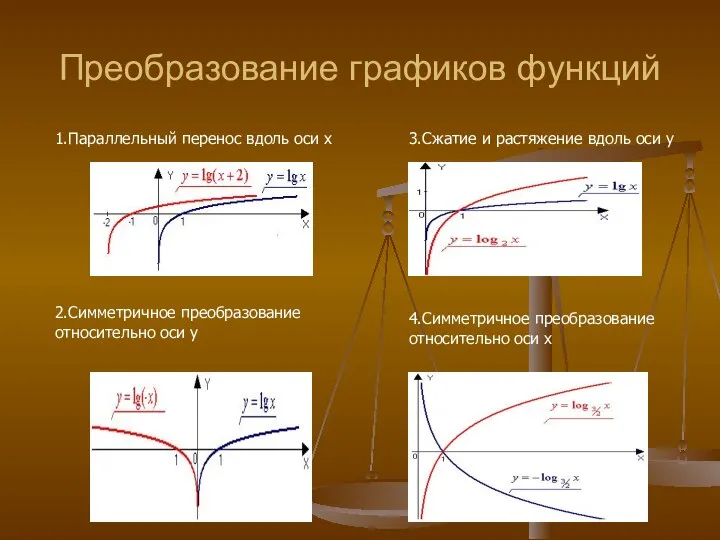
- 41. Преобразование графиков функций 1.Параллельный перенос вдоль оси x 3.Сжатие и растяжение вдоль оси y 2.Симметричное преобразование
- 42. Сжатие ( растяжение ) графика вдоль оси ординат График функции y= b f (x) при b>1
- 43. Перенос вдоль оси ординат График функции y= f (x) + b при b>0 можно получить параллельным
- 44. Перенос вдоль оси абсцисс График функции y=f(x + c) можно получить параллельным переносом вдоль оси абсцисс
- 45. Симметрия относительно оси абсцисс 0 1 x y=x2 y=-x2 Чтобы построить график функции y= -f(x): 1.
- 46. Фото отчет
- 47. Над презентацией старались: Мухаметшина Регина Насырова Эльвира Сибагатова Лейля
- 49. Скачать презентацию


























![D (f) = [ - 3; 6] E (f) = [1;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1459476/slide-32.jpg)











 Параллельные прямые
Параллельные прямые Умножение десятичных дробей на натуральное число
Умножение десятичных дробей на натуральное число Площадь поверхности
Площадь поверхности Введение в геометрию
Введение в геометрию Деление дробей. Путешествие в Китай. 5 класс
Деление дробей. Путешествие в Китай. 5 класс Брейн - ринг. Математическая игра
Брейн - ринг. Математическая игра Основные геометрические приложения определенного интеграла
Основные геометрические приложения определенного интеграла Обобщающий урок по теме: «Признаки параллельности прямых»
Обобщающий урок по теме: «Признаки параллельности прямых» Презентация по математике "Соотношение углов и сторон прямоугольного треугольника" - скачать
Презентация по математике "Соотношение углов и сторон прямоугольного треугольника" - скачать  Тренажёр. Табличное умножение
Тренажёр. Табличное умножение ЕГЭ. Производная в заданиях уровня В. 2 часть
ЕГЭ. Производная в заданиях уровня В. 2 часть Елементи теорії формальних мов. (Тема 2)
Елементи теорії формальних мов. (Тема 2) Среднее арифметическое в поисках сокровищ
Среднее арифметическое в поисках сокровищ Как нарисовать многоконечную звезду
Как нарисовать многоконечную звезду Описанная и вписанная окружности треугольника
Описанная и вписанная окружности треугольника Числовые функции, свойства функции, 10 класс
Числовые функции, свойства функции, 10 класс Опис досвіду УЧАСНИКА КОНКУРСУ «УЧИТЕЛЬ РОКУ» Чим приваблює робота в школі: Поряд з молоддю – молодію душею.
Опис досвіду УЧАСНИКА КОНКУРСУ «УЧИТЕЛЬ РОКУ» Чим приваблює робота в школі: Поряд з молоддю – молодію душею. Пирамида
Пирамида Комбинаторика. Комбинаторные задачи
Комбинаторика. Комбинаторные задачи Дивергентные математические задачи как средство развития креативности мышления у младших школьников
Дивергентные математические задачи как средство развития креативности мышления у младших школьников Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Презентация на тему Решение задач нахождение числа по его дроби
Презентация на тему Решение задач нахождение числа по его дроби  Генетический подход в изучении геометрии
Генетический подход в изучении геометрии Универсальные учебные действия на уроках математики
Универсальные учебные действия на уроках математики Математическое моделирование социальноэкономических процессов (Часть 1.)
Математическое моделирование социальноэкономических процессов (Часть 1.) Подготовка к ЕГЭ (профильный уровень). Теория вероятности
Подготовка к ЕГЭ (профильный уровень). Теория вероятности 8, 9 сандарына көбейту және бөлу кестесі
8, 9 сандарына көбейту және бөлу кестесі Параллельное проектирование
Параллельное проектирование