Содержание
- 2. Теория графов Лектор: Гладких Борис Афанасьевич, профессор кафедры прикладной информатики Gladkikh_ba@yahoo.com Факультет информатики, 2016
- 3. Введение Теория графов – раздел дискретной математики, изучающий свойства конечных или счетных множеств с точки зрения
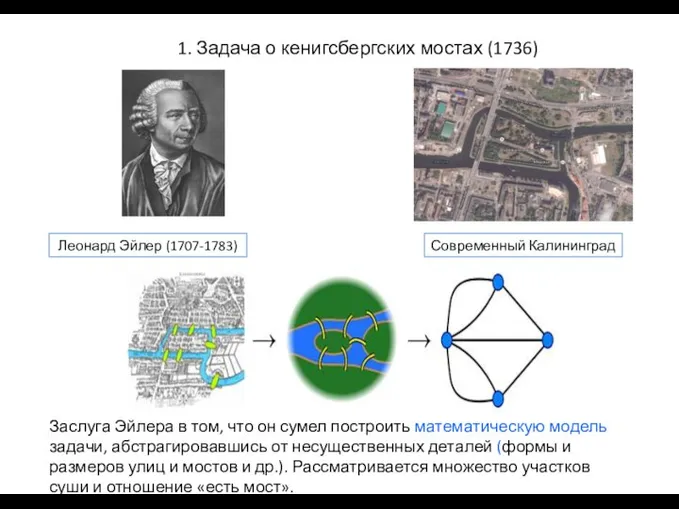
- 4. Леонард Эйлер (1707-1783) 1. Задача о кенигсбергских мостах (1736) Современный Калининград Заслуга Эйлера в том, что
- 5. Впервые понятие «граф» ввел в 1936 году венгерский математик Денеш Кëниг. Он же написал первую книгу
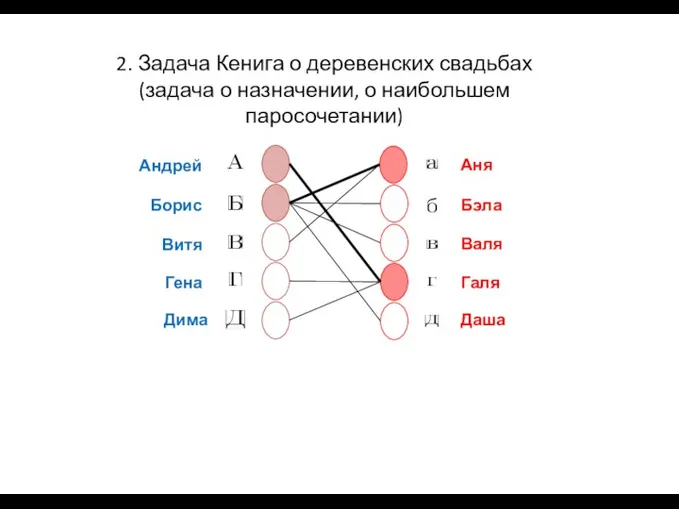
- 6. 2. Задача Кенига о деревенских свадьбах (задача о назначении, о наибольшем паросочетании) Андрей Борис Витя Гена
- 7. 3. Задача о раскраске плоского графа (проблема четырех красок) Задача поставлена в 1852(?) г. шотландским физиком
- 8. В 1976 г. ведущие математики всего мира получили письма с почтовым штемпелем «Четырех красок достаточно». В
- 9. Во 2-й половине 20 века теория графов превратилась в разветвленную математическую дисциплину, имеющую множество приложений: в
- 10. Глава 1. Основные понятия
- 11. 1.1. Типы графов. Основная терминология
- 12. Терминология теории графов очень разнообразна и не окончательно устоялась. Почти каждый автор начинает учебник с объяснения
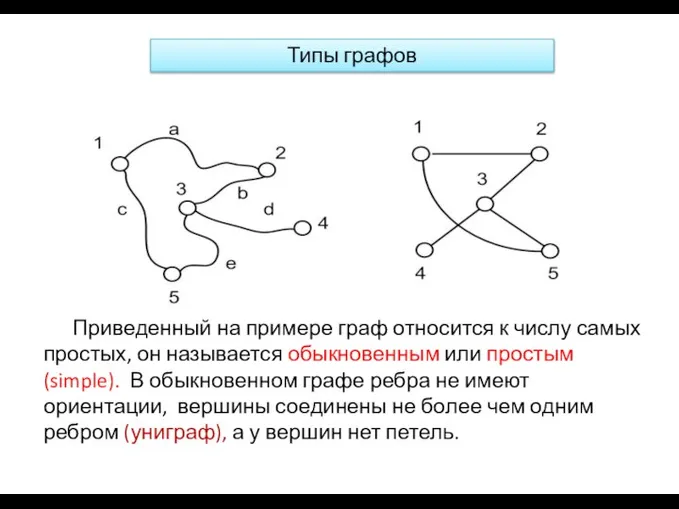
- 13. Приведенный на примере граф относится к числу самых простых, он называется обыкновенным или простым (simple). В
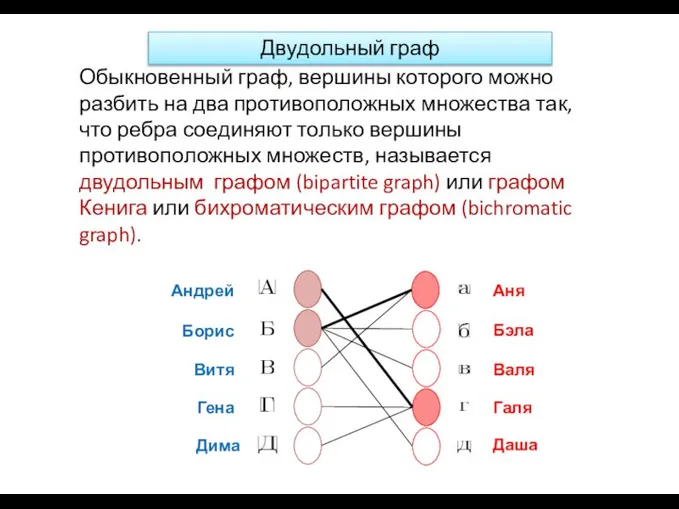
- 14. Андрей Борис Витя Гена Дима Аня Бэла Валя Галя Даша Обыкновенный граф, вершины которого можно разбить
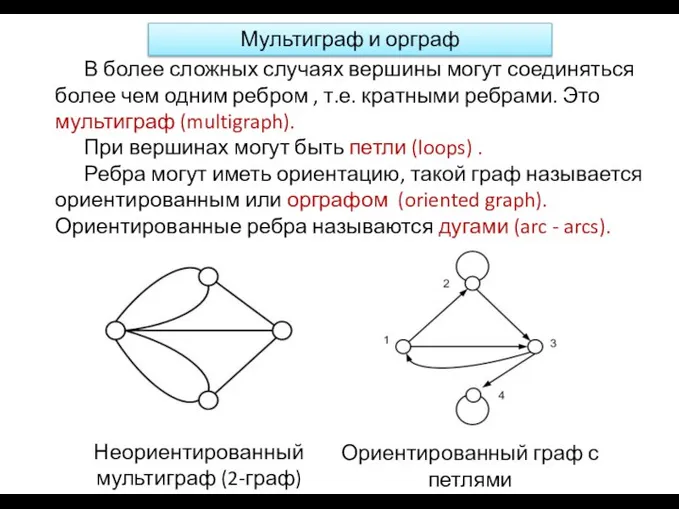
- 15. Неориентированный мультиграф (2-граф) Ориентированный граф с петлями В более сложных случаях вершины могут соединяться более чем
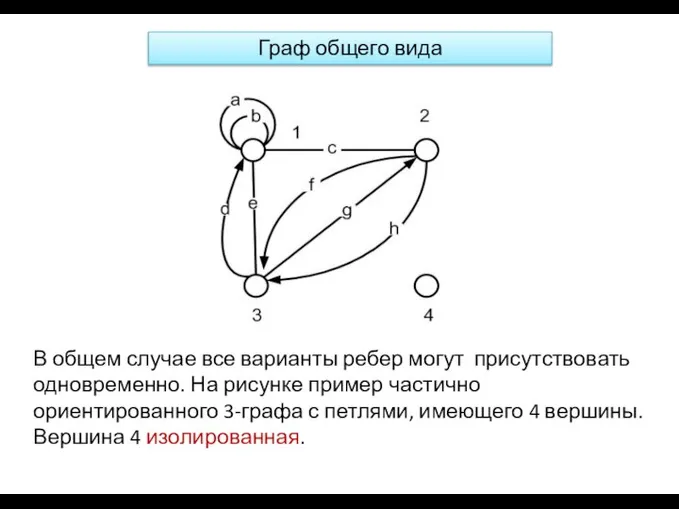
- 16. В общем случае все варианты ребер могут присутствовать одновременно. На рисунке пример частично ориентированного 3-графа с
- 17. В некоторых графовых моделях ребрам приписываются некоторые числа (веса ), которые означают длины ребер, пропускные способности
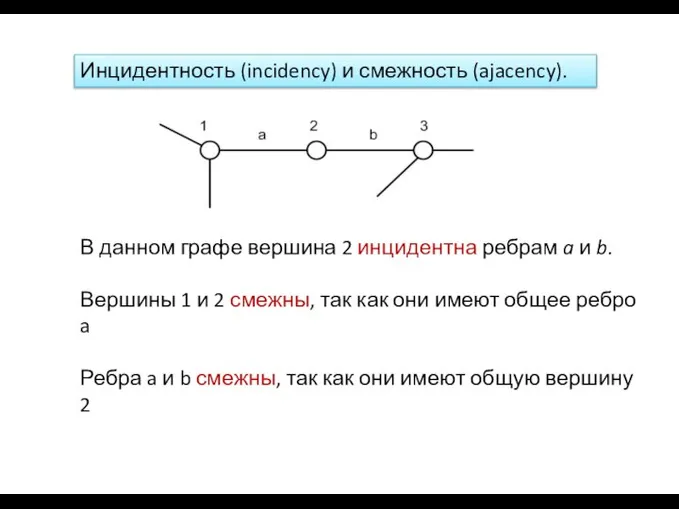
- 18. Инцидентность (incidency) и смежность (ajacency). В данном графе вершина 2 инцидентна ребрам a и b. Вершины
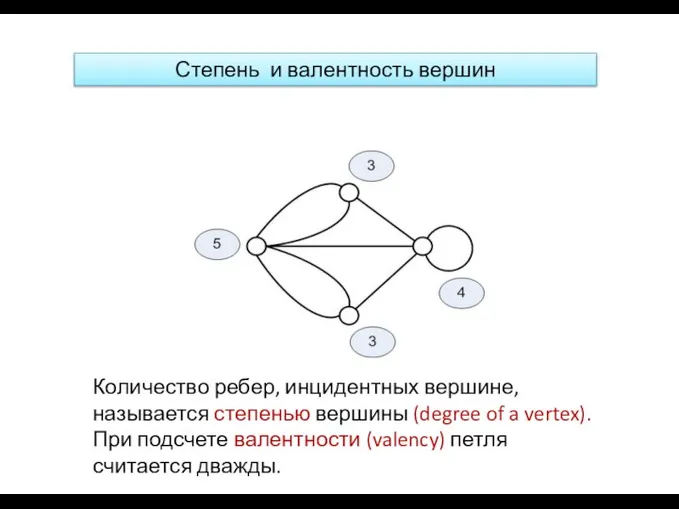
- 19. Степень и валентность вершин Количество ребер, инцидентных вершине, называется степенью вершины (degree of a vertex). При
- 20. 1.2. Части графа
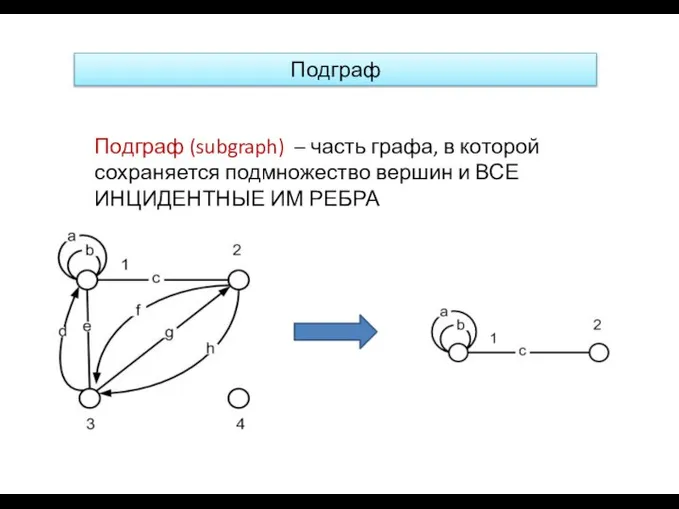
- 21. Подграф Подграф (subgraph) – часть графа, в которой сохраняется подмножество вершин и ВСЕ ИНЦИДЕНТНЫЕ ИМ РЕБРА
- 22. Пустой подграф
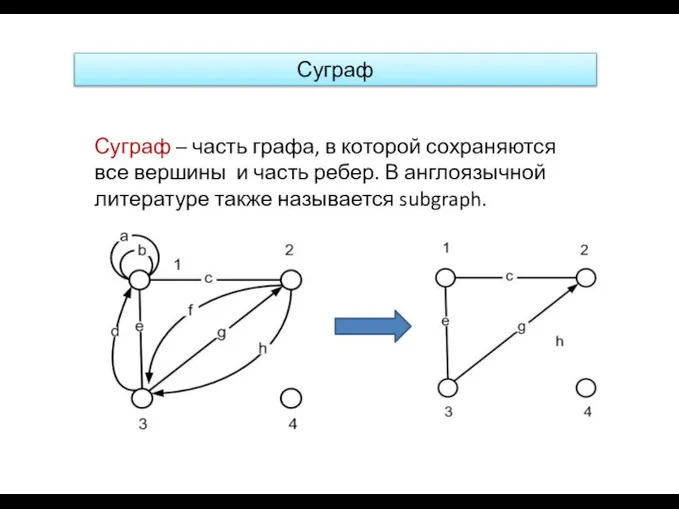
- 23. Суграф Суграф – часть графа, в которой сохраняются все вершины и часть ребер. В англоязычной литературе
- 24. 1.3. Математическое определение графа
- 25. Для понятия «граф» существуют несколько строгих математических определений, каждое из которых удобно для определенного класса графов:
- 26. Обыкновенный граф Пример
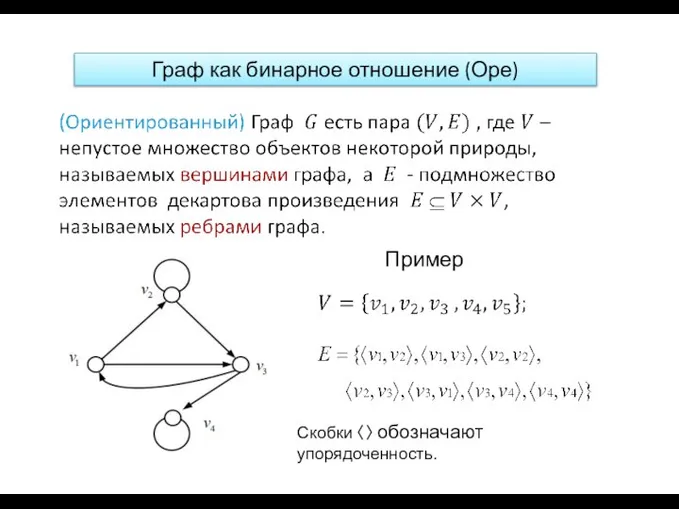
- 27. Граф как бинарное отношение (Оре) Пример Скобки 〈〉 обозначают упорядоченность.
- 29. Ойстин Оре (1899—1968) Определение графа -- бинарного отношения использует норвежский математик О. Оре в монографии «Теория
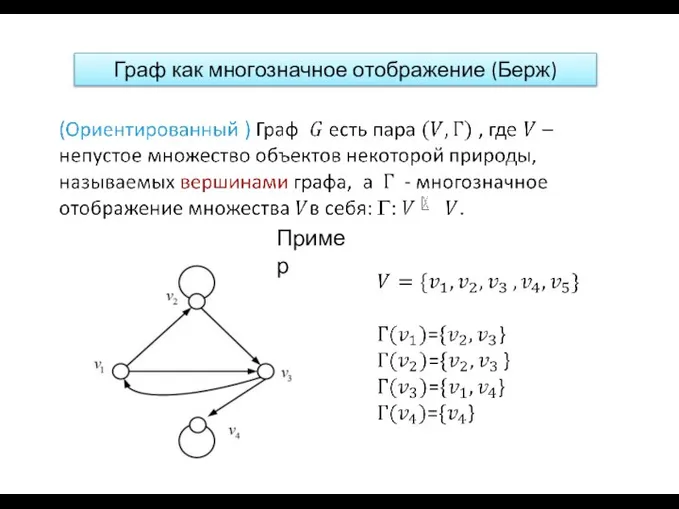
- 30. Граф как многозначное отображение (Берж) Пример
- 31. -
- 33. Claude Jacques Berge (5 June 1926 – 30 June 2002) was a French mathematician, recognized as
- 34. Граф общего вида как трехместный предикат (Зыков)
- 35. 1. 2. 3.
- 37. Это определение охватывает все виды графов – ориентированные и неориентированные, униграфы и мультиграфы.
- 38. Зыков, Александр Александрович (1922—2013)
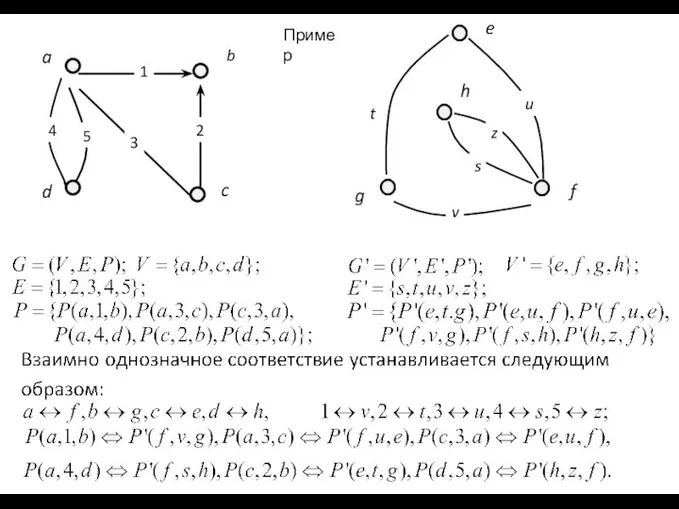
- 39. Изоморфизм графов
- 40. t Пример
- 41. . Тем самым оказываются несущественными как природа элементов, составляющих множества V и E , так и
- 42. Способы задания графов
- 43. 1.4. Задание графа матрицами
- 44. Матрица инциденций
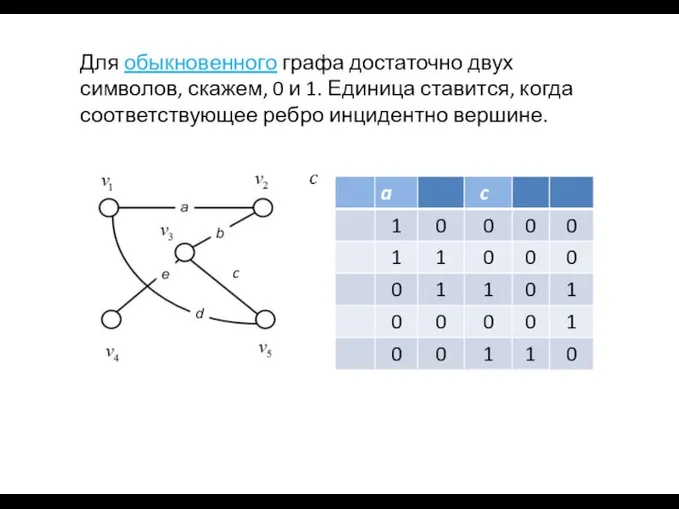
- 45. Для обыкновенного графа достаточно двух символов, скажем, 0 и 1. Единица ставится, когда соответствующее ребро инцидентно
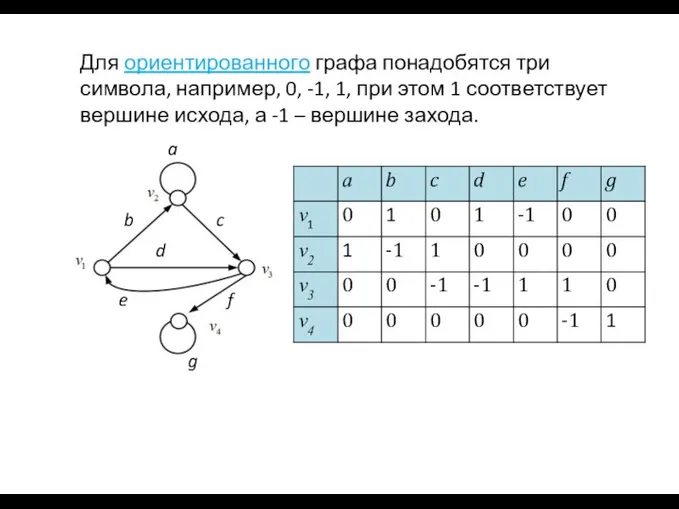
- 46. Для ориентированного графа понадобятся три символа, например, 0, -1, 1, при этом 1 соответствует вершине исхода,
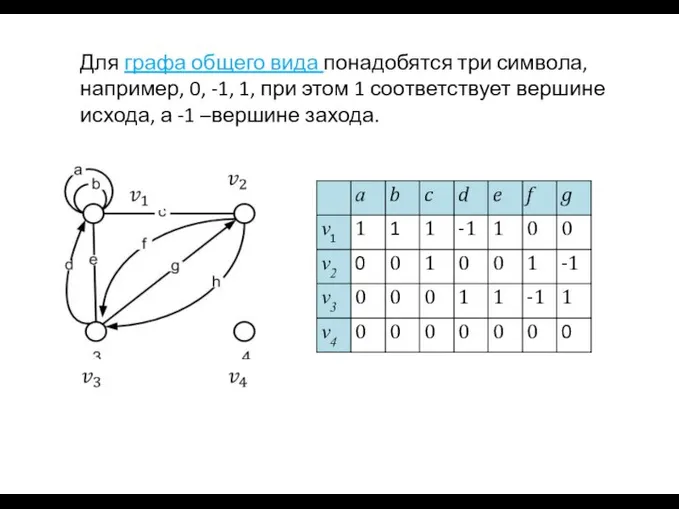
- 47. Для графа общего вида понадобятся три символа, например, 0, -1, 1, при этом 1 соответствует вершине
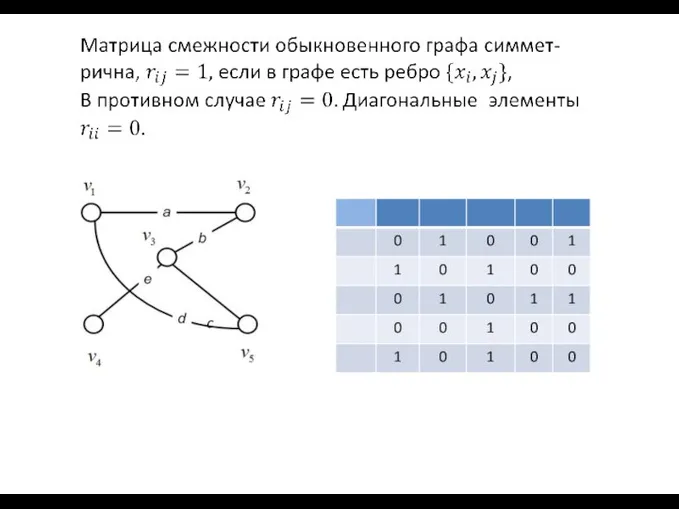
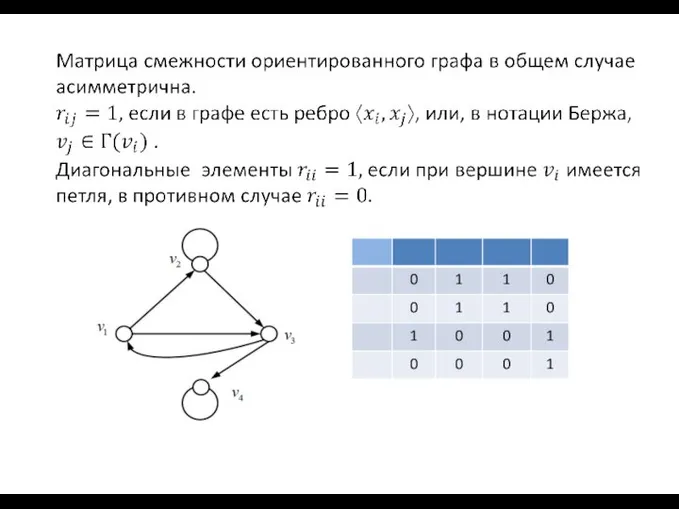
- 48. Матрица смежности
- 49. c
- 50. c
- 52. Скачать презентацию































 Понятие функции
Понятие функции Задачи на построение
Задачи на построение Прямоугольный параллелепипед. Задания для устного счета. Упражнение 9
Прямоугольный параллелепипед. Задания для устного счета. Упражнение 9 Парная регрессия и корреляция
Парная регрессия и корреляция Презентация по математике "Координаты на поле" - скачать
Презентация по математике "Координаты на поле" - скачать  Как мы используем математику в жизни
Как мы используем математику в жизни Піраміда. Види пірамід. Площа поверхні. Об`єм
Піраміда. Види пірамід. Площа поверхні. Об`єм Накопленная частота и др
Накопленная частота и др Изометрическая проекция окружности
Изометрическая проекция окружности Задачи по эпюрам 3 и 4. Пересечение конуса и цилиндра
Задачи по эпюрам 3 и 4. Пересечение конуса и цилиндра Презентация по математике "Умножение на 1 и 0" - скачать бесплатно
Презентация по математике "Умножение на 1 и 0" - скачать бесплатно Степени и корни
Степени и корни Решение уравнений с модулем
Решение уравнений с модулем Теорема Пифагора. Задачи
Теорема Пифагора. Задачи Фракталы в биологии
Фракталы в биологии Икосаэдр. Виды икосаэдров
Икосаэдр. Виды икосаэдров Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Разработка технологических карт и протоколов уроков по учебному предмету «математика»
Разработка технологических карт и протоколов уроков по учебному предмету «математика» Логарифмические неравенства. (11 класс)
Логарифмические неравенства. (11 класс) Аксиома параллельных прямых 27.03.2012
Аксиома параллельных прямых 27.03.2012  Различные формы записи комплексных чисел. Операции над комплексными числами в тригонометрической и показательной формах
Различные формы записи комплексных чисел. Операции над комплексными числами в тригонометрической и показательной формах Арифметическая прогрессия
Арифметическая прогрессия Применение производной для исследования функций на монотонность
Применение производной для исследования функций на монотонность Системы ходов. Виды теодолитных ходов
Системы ходов. Виды теодолитных ходов Сумма углов в треугольнике. Неравенство треугольника
Сумма углов в треугольнике. Неравенство треугольника Комплексные чертежи прямых линий
Комплексные чертежи прямых линий Центральная и осевая симметрия
Центральная и осевая симметрия Дискретная математика. Алгебра Жегалкина
Дискретная математика. Алгебра Жегалкина