Содержание
- 2. Кривые второго порядка делятся на вырожденные и невырожденные. Вырожденные кривые второго порядка это прямые, которые задаются
- 3. Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять
- 4. Это множество точек на плоскости, сумма расстояний от каждой из которых до двух заданных точек плоскости
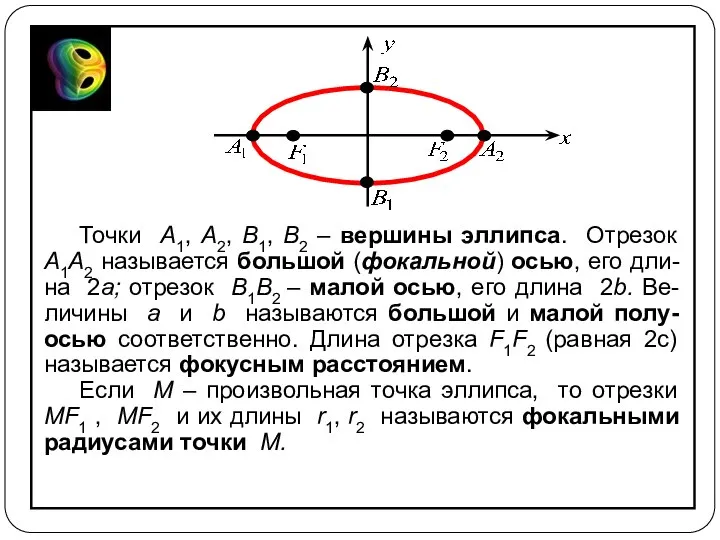
- 5. Точки A1, A2, B1, B2 – вершины эллипса. Отрезок A1A2 называется большой (фокальной) осью, его дли-на
- 6. СВОЙСТВА ЭЛЛИПСА 1) Эллипс лежит внутри прямоугольника, ограни- ченного прямыми x=±a, y=±b. 2) Эллипс имеет центр
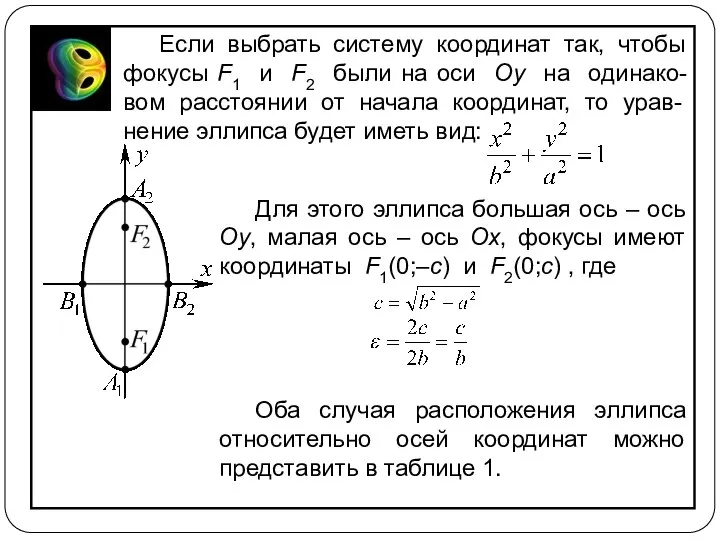
- 7. Если выбрать систему координат так, чтобы фокусы F1 и F2 были на оси Oy на одинако-вом
- 8. Это множество точек на плоскости, разность расстояний от каждой из которых до двух заданных точек плоскости
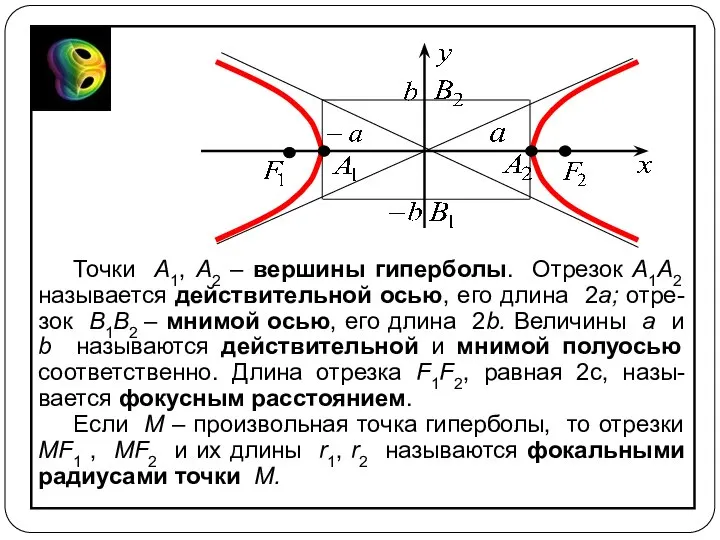
- 9. Точки A1, A2 – вершины гиперболы. Отрезок A1A2 называется действительной осью, его длина 2a; отре-зок B1B2
- 10. СВОЙСТВА ГИПЕРБОЛЫ 1) В полосе, ограниченной прямыми x=±a, точек гиперболы нет. 2) Гипербола имеет центр симметрии
- 11. Если в уравнении гиперболы a=b, то гипербола назы-вается равнобочной и ее уравнение имеет вид: или .
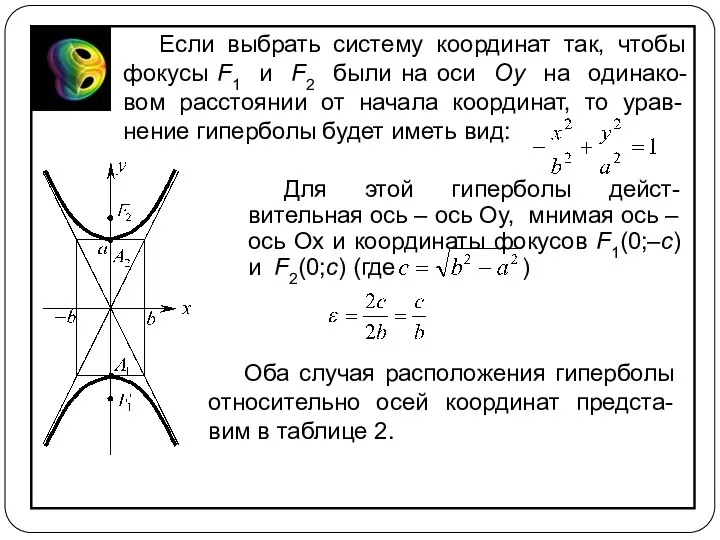
- 12. Если выбрать систему координат так, чтобы фокусы F1 и F2 были на оси Oy на одинако-вом
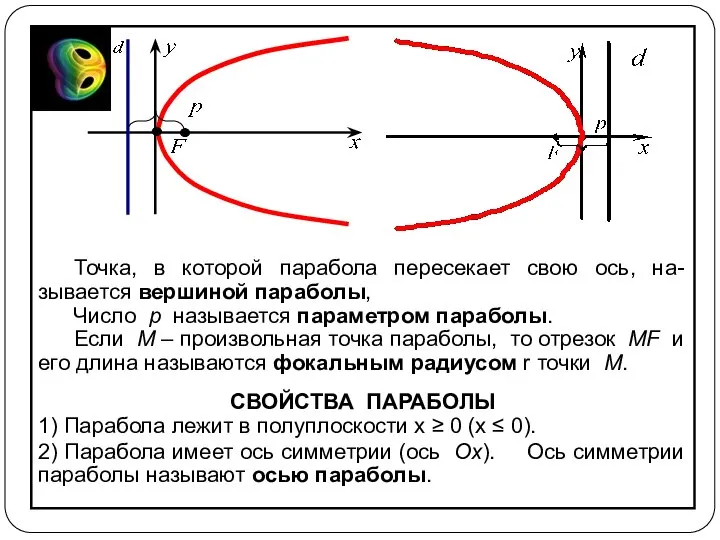
- 13. Это множество точек на плоскости, равноудаленных от заданной точки (называемой фокусом) и данной прямой d, называемой
- 14. Точка, в которой парабола пересекает свою ось, на-зывается вершиной параболы, Число p называется параметром параболы. Если
- 16. Скачать презентацию








 Преобразование выражений, содержащих квадратные корни
Преобразование выражений, содержащих квадратные корни Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Введение декартовых координат в пространстве. Формулы середины отрезка и расстояния между двумя точками
Введение декартовых координат в пространстве. Формулы середины отрезка и расстояния между двумя точками Решение заданий С1, С3
Решение заданий С1, С3 Взаимное положение прямой линии и плоскости, плоскостей. (Лекция 4)
Взаимное положение прямой линии и плоскости, плоскостей. (Лекция 4) Solid geometry
Solid geometry Система уравнений. Решение систем способом сложения
Система уравнений. Решение систем способом сложения Решение квадратных уравнений
Решение квадратных уравнений Десятичные дроби. Исторический материал
Десятичные дроби. Исторический материал Аксиомы стереометрии и их следствия
Аксиомы стереометрии и их следствия Метод рационализации
Метод рационализации Фракталы в аэрографии
Фракталы в аэрографии Аттестационная работа. Рабочая программа Юный шахматист
Аттестационная работа. Рабочая программа Юный шахматист Рисуем по координатам
Рисуем по координатам Применение презентаций на уроках математики как один из способов повышения интереса к учебе
Применение презентаций на уроках математики как один из способов повышения интереса к учебе Основы математического планирования эксперимента
Основы математического планирования эксперимента Леонардо по прозвищу Фибоначчи
Леонардо по прозвищу Фибоначчи Презентация по математике "Что такое пирамида ?" - скачать
Презентация по математике "Что такое пирамида ?" - скачать  Функции и их графики
Функции и их графики Задачи и упражнения на готовых чертежах 10 класс Глава 1. Параллельность прямых и плоскостей к учебнику «Геометрия 10-11» Автор Л.
Задачи и упражнения на готовых чертежах 10 класс Глава 1. Параллельность прямых и плоскостей к учебнику «Геометрия 10-11» Автор Л. Решение алгебраических уравнений Выполнил: Нелюбин Алексей 9 «В» класс Школа№3 г. Свирск
Решение алгебраических уравнений Выполнил: Нелюбин Алексей 9 «В» класс Школа№3 г. Свирск Урок 6. Перколяционные процессы
Урок 6. Перколяционные процессы Методика работы с задачей на круговое движение
Методика работы с задачей на круговое движение Сложение чисел с разными знаками. Верные равенства
Сложение чисел с разными знаками. Верные равенства Графические методы исследования
Графические методы исследования Застосування різних способів до розкладу многочлена на множники
Застосування різних способів до розкладу многочлена на множники Двузначные числа
Двузначные числа Сума кутів трикутника. Урок розв'язування задач. 7 клас
Сума кутів трикутника. Урок розв'язування задач. 7 клас