Содержание
- 2. Тема: Дифференциальное исчисление функции одной переменной
- 3. §1. Производная функции ОПР. Производной функции y = f (x) в точке x называется предел отношения
- 4. Функция, имеющая конечную производную в точке, называется дифференцируемой в этой точке, а операция нахождения производной называется
- 5. Связь дифференцируемости и непрерывности функции Если функция дифференцируема в данной точке, то она непрерывна в ней.
- 6. 1.1. Техника дифференцирования Правила дифференцирования Пусть и дифференцируемые функции независимой переменной x,
- 7. Таблица производных
- 9. Пример Найти производные первого порядка функций 1). Решение. Применим формулу производной суммы Далее используем формулы:
- 10. (1): (3): (1): Правило (1): Тогда:
- 11. 2) Решение. Используем правило дифференцирования произведения Далее, по таблице производных имеем: Формула (5): Формула (10):
- 13. 3) Производная сложной функции. Вычислить производную Решение. Используем формулу В данном случае Тогда:
- 14. 1.2. Дифференциал функции Пусть функция имеет в точке x производную Тогда где при
- 15. Причем, Слагаемое - главная часть приращения функции .
- 16. ОПР. Дифференциалом функции в точке называется главная часть приращения функции, равная произведению производной функции на приращение
- 17. 1.3. Геометрический смысл производной Производная от функции в точке равна угловому коэффициенту касательной к графику функции
- 18. 1.4. Уравнения касательной и нормали Уравнение касательной можно найти, используя уравнение прямой, проходящей через данную точку
- 19. Уравнение нормали Прямая перпендикулярная касательной в точке касания называется нормалью к кривой. Угловые коэффициенты касательной и
- 20. Потому уравнение нормали в точке имеет вид: Углом между кривыми называют угол между касательными к кривым
- 21. Экономический смысл производной. Эластичность Пусть функция u=u(t) выражает количество произведенной продукции u за время t. Необходимо
- 22. Средняя производительность труда за этот период времени: ОПР. Производительностью труда в момент называется предельное значение средней
- 23. ОПР. Эластичностью функции y=f(x) в точке x называется предел Эластичность функции показывает на сколько процентов изменится
- 24. Пусть D=D(p) – функция спроса (зависит от цены товара p). Тогда под эластичностью спроса понимается процентное
- 26. Скачать презентацию








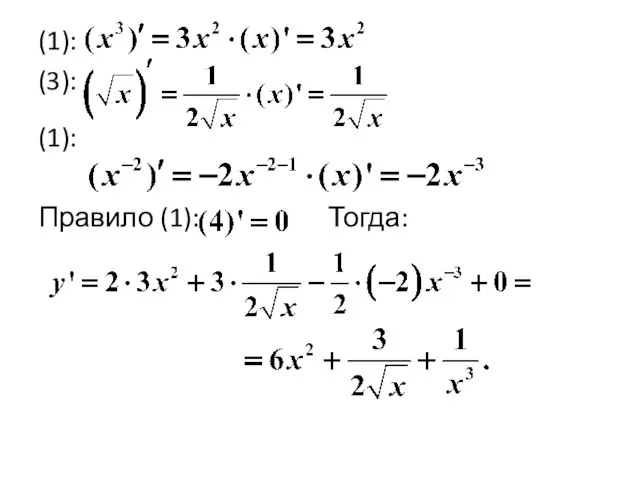














 Первый признак подобия треугольников
Первый признак подобия треугольников Графы. Раскраска графов. (Тема 3)
Графы. Раскраска графов. (Тема 3) Исследование функций с помощью производной
Исследование функций с помощью производной Диофант и его уравнения Автор: Потапова Софья 10 класс, МОУ гимназия № 63 Научный руководитель: Багина Татьяна Александровна, учит
Диофант и его уравнения Автор: Потапова Софья 10 класс, МОУ гимназия № 63 Научный руководитель: Багина Татьяна Александровна, учит Диалоги о параболе. 9 класс
Диалоги о параболе. 9 класс Признаки подобия треугольников
Признаки подобия треугольников Погрешности измерений. Лекция 5
Погрешности измерений. Лекция 5 Статистика как наука
Статистика как наука Равные выражения. Сравниваем выражения
Равные выражения. Сравниваем выражения Производная в исследовании функций
Производная в исследовании функций Нахождение дроби и процентов от числа
Нахождение дроби и процентов от числа Необходимые и достаточное условия идентифицируемости СОУ. Косвенный метод наименьших квадратов
Необходимые и достаточное условия идентифицируемости СОУ. Косвенный метод наименьших квадратов Аттестационная работа. Программа внеурочной деятельности Реальная математика
Аттестационная работа. Программа внеурочной деятельности Реальная математика Экономические индексы
Экономические индексы Разложение на множители с помощью группировки
Разложение на множители с помощью группировки Презентация на тему Закрепление письменных приемов сложения и вычитания 2 класс
Презентация на тему Закрепление письменных приемов сложения и вычитания 2 класс Математика в моей будущей профессии металлурга
Математика в моей будущей профессии металлурга Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Трапеция и ее свойства
Трапеция и ее свойства Геометрическая прогрессия. Задачи
Геометрическая прогрессия. Задачи Домашнее задание. Геометрия
Домашнее задание. Геометрия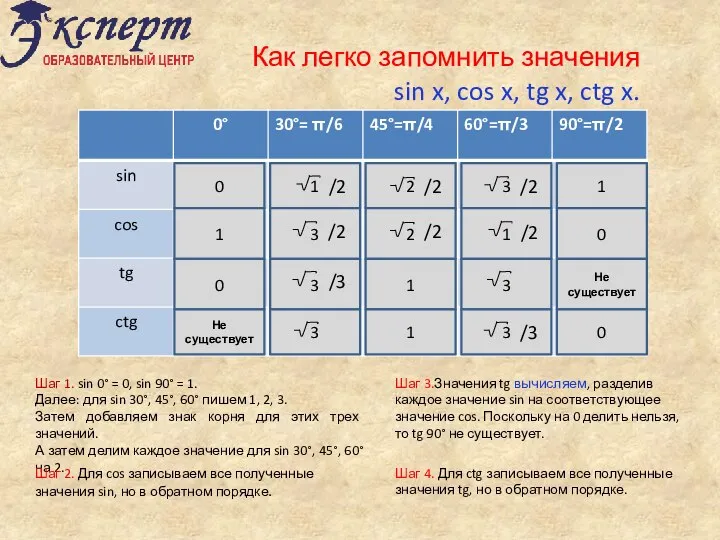 Как легко запомнить значения sin x, cos x, tg x, ctg x
Как легко запомнить значения sin x, cos x, tg x, ctg x Деление с остатком
Деление с остатком Транспортная задача. (Лекции 10,11)
Транспортная задача. (Лекции 10,11) Объемы тел
Объемы тел Методы решения уравнений
Методы решения уравнений Своя игра по математике
Своя игра по математике Решение задач на составление линейных алгоритмов
Решение задач на составление линейных алгоритмов