Содержание
- 2. План лекции Определитель 2-го порядка. Определитель n-го порядка. Свойства определителя. Основные методы вычисления определителя: метод приведения
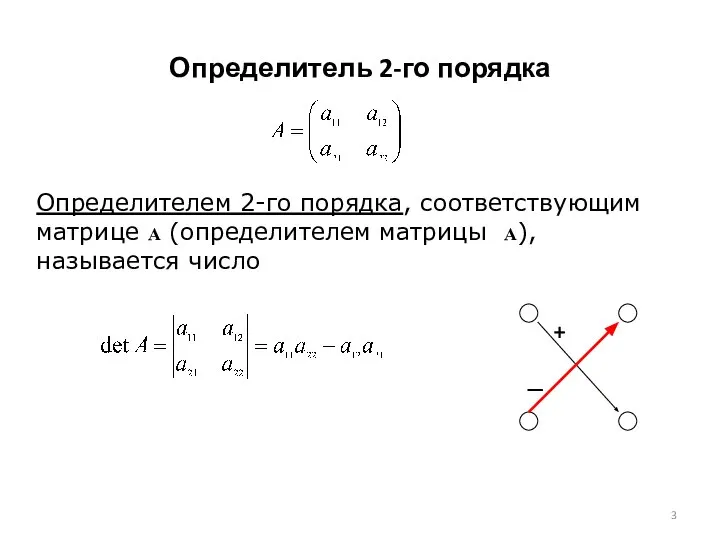
- 3. Определитель 2-го порядка Определителем 2-го порядка, соответствующим матрице A (определителем матрицы А), называется число
- 4. Примеры вычисления определителя 2-го порядка 1) 2)
- 5. Определитель n-го порядка Определителем n-го порядка, соответствующим матрице A, называется число detA, равное сумме всех произведений
- 6. Число t (s) равно числу транспозиций, которое нужно сделать, чтобы перейти от основной перестановки (1,2,…,n) к
- 7. Свойства определителя Умножение некоторой строки (столбца) матрицы определителя на некий коэффициент равносильно умножению самого определителя на
- 8. Свойства определителя Если все элементы некоторой строки (столбца) матрицы равны нулю, то и определитель равен нулю.
- 9. Свойства определителя Если к некоторой строке (столбцу) определителя прибавить другую строку (столбец), умноженную на произвольное число,
- 10. Свойства определителя Алгебраическим дополнением элемента называется следующий определитель n-го порядка i-ая строка j-й столбец
- 11. Свойства определителя 9. Сумма произведений элементов любой строки (столбца) определителя на их алгебраические дополнения равна этому
- 12. умножение строки (столбца) на число, отличное от нуля; прибавление к одной строке (столбцу) другой, умноженной на
- 13. Методы вычисления определителей 1. Метод приведения к треугольному виду Матрица определителя приводится элементарными преобразованиями над строками
- 14. Методы вычисления определителей 2. Метод понижения порядка Минором , соответствующим элементу определителя n-го порядка, называется определитель
- 15. Линейная алгебра Лекция 2 Обратная матрица
- 16. План лекции Определение обратной матрицы Свойства обратимой матрицы Вырожденная и невырожденная матрицы Необходимое и достаточное условие
- 17. ОБРАТНАЯ МАТРИЦА Квадратная матрица А называется обратимой, если найдётся квадратная матрица В такая, что выполняются равенства:
- 18. НЕКОТОРЫЕ СВОЙСТВА ОБРАТИМЫХ МАТРИЦ Если квадратные матрицы А и В обратимы, то справедливы следующие соотношения:
- 19. Вырожденные и невырожденные матрицы Матрица А называется невырожденной, если определитель матрицы отличен от нуля, и вырожденной
- 20. Для того чтобы для матрицы А существовала обратная, необходимо и достаточно, чтобы определитель матрицы был отличен
- 21. Основные методы построения обратной матрицы. Метод присоединенной матрицы Присоединенная матрица определяется как транспонированная к матрице, составленной
- 23. Скачать презентацию



















 Алгебра, 11 класс (задачи)
Алгебра, 11 класс (задачи) Деление степеней
Деление степеней Конус. Означення та елементи конуса. Перерізи конуса. (11 клас)
Конус. Означення та елементи конуса. Перерізи конуса. (11 клас) Примеры комбинаторных задач
Примеры комбинаторных задач Подобные треугольники
Подобные треугольники Формула бинома Ньютона. Свойства биномиальных коэффициентов
Формула бинома Ньютона. Свойства биномиальных коэффициентов Задачи на умножение
Задачи на умножение Обыкновенные дроби. Смешанные дроби. Математика 5 класс. Учитель математики 1 квалификационной катег
Обыкновенные дроби. Смешанные дроби. Математика 5 класс. Учитель математики 1 квалификационной катег Арифметическая прогрессия
Арифметическая прогрессия Умножение смешанных чисел
Умножение смешанных чисел Десятичные дроби
Десятичные дроби Линейные фракталы
Линейные фракталы Презентация "Признаки делимости" 6 класс
Презентация "Признаки делимости" 6 класс Краткие сведения об аппроксимации функций
Краткие сведения об аппроксимации функций Chapter 1. Polynomial and Rational Functions. 3.3. Dividing Polynomials; Remainder and Factor Theorems
Chapter 1. Polynomial and Rational Functions. 3.3. Dividing Polynomials; Remainder and Factor Theorems Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел 2 класс Математический диктант № 2 Выполнила Кирилова С.Г. Учитель начальных классов Школы «Ученики Пифагора» г. Лимассол, р.К
2 класс Математический диктант № 2 Выполнила Кирилова С.Г. Учитель начальных классов Школы «Ученики Пифагора» г. Лимассол, р.К Урок математики
Урок математики  Деление с остатком
Деление с остатком Урок геометрии в 7 классе. Треугольники
Урок геометрии в 7 классе. Треугольники Уравнения. Решение задач с помощью уравнений. 6 класс
Уравнения. Решение задач с помощью уравнений. 6 класс Статистическое оценивание. Выборочный метод. Требования, предъявляемые к выборке. (Лекция 4)
Статистическое оценивание. Выборочный метод. Требования, предъявляемые к выборке. (Лекция 4) Таблица умножения и деления на 3
Таблица умножения и деления на 3 Графика в координатах Автор: Стафеева Елизавета
Графика в координатах Автор: Стафеева Елизавета Прямоугольный треугольник
Прямоугольный треугольник Презентация по математике "Сложение и вычитание двузначныз чисел" - скачать бесплатно
Презентация по математике "Сложение и вычитание двузначныз чисел" - скачать бесплатно Презентация на тему Леонард Эйлер Идеальный математик XVII века
Презентация на тему Леонард Эйлер Идеальный математик XVII века Аксиоматические теории первого порядка
Аксиоматические теории первого порядка