Содержание
- 2. Линейные операторы в линейных пространствах Пусть даны линейные пространства X и Y над одним и тем
- 3. Линейные операторы в линейных пространствах Оператор , действующий из X в Y, называют линейным, если он
- 4. Свойства линейных операторов в линейных пространствах линейный оператор переводит линейную комбинацию векторов из X в линейную
- 5. Пример Пример
- 6. Линейные операторы в линейных пространствах Пусть из линейного пространства X в линейное пространство Y действует линейный
- 7. Линейные операторы в линейных пространствах Множество всех векторов линейного пространства X, которые переводятся линейным оператором в
- 8. Линейные операторы в линейных пространствах Если ядро линейного оператора состоит только из нулевого вектора (т.е. дефект
- 9. Примеры линейных операторов в линейных пространствах Оператор : , переводящий каждый вектор a линейного пространства X
- 10. Линейные операторы в линейных пространствах Теорема Пусть линейный оператор действует из линейного пространства X в линейное
- 11. Линейные операторы в линейных пространствах Если известны образы векторов базиса , то для любого вектора мы
- 12. Линейные операторы и матрицы Предположим, что в линейном пространстве X задан базис , а в линейном
- 13. Линейные операторы и матрицы Матрица (**) называется матрицей линейного оператора в паре базисов и . Утверждение.
- 14. Утверждение. Линейные операторы и матрицы Между множеством линейных операторов, действующих из n - мерного линейного пространства
- 15. Линейные операторы и матрицы Замечание. Если оператор действует в линейном пространстве X, то X выступает и
- 16. Линейные операторы и матрицы Теорема Пусть линейный оператор, действующий из линейного пространства X в линейное пространство
- 17. Выражение координат вектора - образа через координаты вектора - прообраза Теорема Если линейный оператор, действующий из
- 19. Скачать презентацию
















 Что такое задача
Что такое задача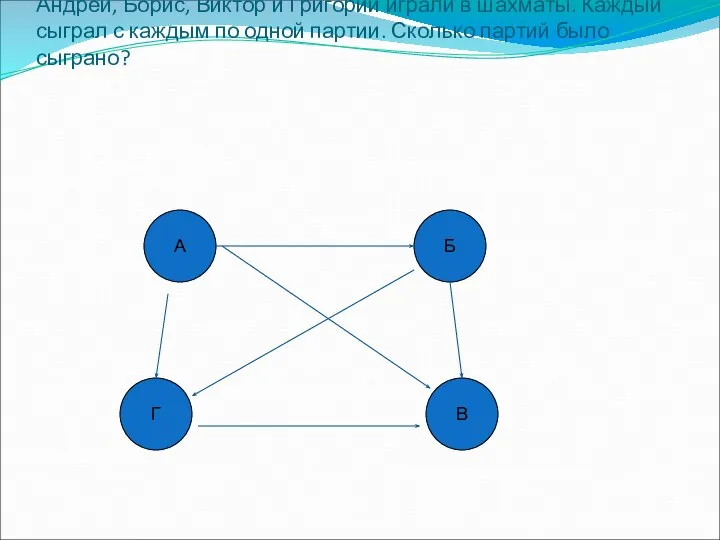 Решение задач с помощью графов
Решение задач с помощью графов Треугольники. Итоговое повторение. 9 класс
Треугольники. Итоговое повторение. 9 класс Методы Монте-Карло
Методы Монте-Карло Мешко Іван Васильович
Мешко Іван Васильович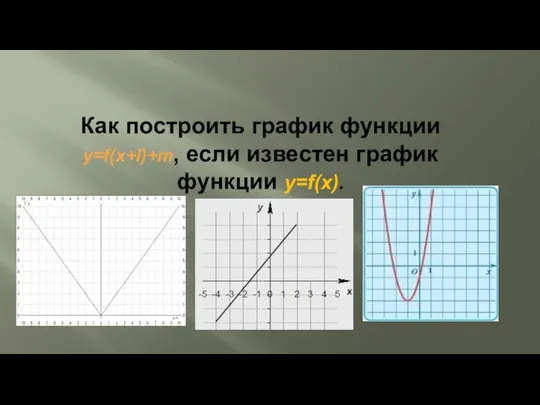 Как построить график функции y=f(x+l)+m, если известен график функции y=f(x)
Как построить график функции y=f(x+l)+m, если известен график функции y=f(x) Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности Интерактивная игра-тренажёр по теме: «Сложение и вычитание в пределах 20». Математика 2 класс
Интерактивная игра-тренажёр по теме: «Сложение и вычитание в пределах 20». Математика 2 класс Алгебра логики
Алгебра логики Правила выполнения и оформления чертежей
Правила выполнения и оформления чертежей Математический паркет
Математический паркет Игра. Счёт в пределах трех
Игра. Счёт в пределах трех Подобные треугольники. Задачи на готовых чертежах (8 класс)
Подобные треугольники. Задачи на готовых чертежах (8 класс) Особые приёмы решения логарифмических неравенств с переменной в основании
Особые приёмы решения логарифмических неравенств с переменной в основании Тригонометрические функции. Зачет по теме
Тригонометрические функции. Зачет по теме Algebra. Natural Integers rational Numbers
Algebra. Natural Integers rational Numbers Разложение многочлена на множители способом группировки
Разложение многочлена на множители способом группировки Производная сложной функции
Производная сложной функции Дифференциальные уравнения и ряды. Лекция 8
Дифференциальные уравнения и ряды. Лекция 8 Интерполяция функций
Интерполяция функций Логарифмическая производная. Производные высших порядков. Теоремы Роля, Лагранжа, Коши. Правило Лопиталя. (Лекция 6)
Логарифмическая производная. Производные высших порядков. Теоремы Роля, Лагранжа, Коши. Правило Лопиталя. (Лекция 6) Системы уравнений. Основные способы их решения. 9 класс
Системы уравнений. Основные способы их решения. 9 класс Тема урока : «Модуль числа»
Тема урока : «Модуль числа»  Площадь прямоугольника
Площадь прямоугольника Параллель және ортогональ проекциялау. Ортогональ проекцияның ауданы
Параллель және ортогональ проекциялау. Ортогональ проекцияның ауданы Решение нестандартных задач в рамках итогового повторения курса алгебры и начала анализа
Решение нестандартных задач в рамках итогового повторения курса алгебры и начала анализа Антагонистические игры
Антагонистические игры Мастер-класс «Использование игровых ситуаций на уроках геометрии при подготовке к ГИА»
Мастер-класс «Использование игровых ситуаций на уроках геометрии при подготовке к ГИА»