Содержание
- 2. Тема 2. Несобственные интегралы Определенный интеграл где [a, b] − конечный промежуток интегрирования, а подынтегральная функция
- 3. §1. Несобственный интеграл I рода (интеграл с бесконечным промежутком интегрирования) Пусть функция f(x) непрерывна на промежутке
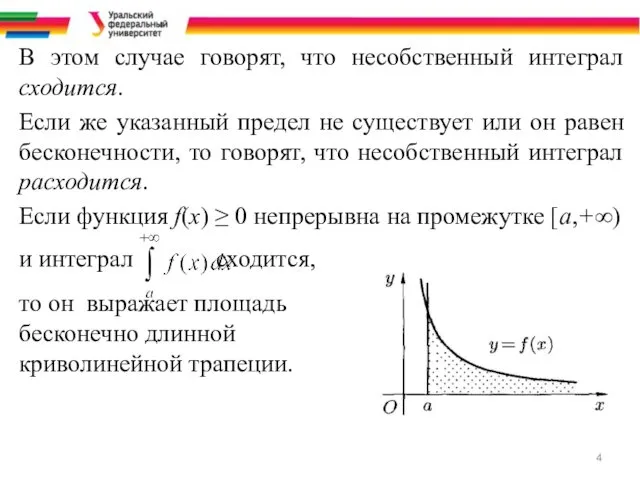
- 4. В этом случае говорят, что несобственный интеграл сходится. Если же указанный предел не существует или он
- 5. Аналогично определяется несобственный интеграл на промежутке (‒∞, b]: Несобственный интеграл с двумя бесконечными пределами определяется формулой:
- 6. Пример 1. Вычислить несобственные интегралы или установить их расходимость: Решение. 1. Вычисляем по определению Интеграл равен
- 7. 3. Разбиваем интеграл на сумму двух несобственных интегралов (для упрощения вычислений возьмем с = 0) Вычисляем
- 8. При решении задач в некоторых случаях нет необходимости вычислять интеграл, достаточно лишь знать сходится он или
- 9. Пример 2. Исследовать на сходимость Решение. Для сравнения используем интеграл который сходится (см. пример 1). Сравним
- 10. 2. Предельный признак сравнения Если на промежутке [a, +∞) f(x) > 0, g(x) > 0 и
- 11. Пример 3. Исследовать на сходимость Решение. Подберем функцию для сравнения. Для этого преобразуем подынтегральную функцию Используем
- 12. По предельному признаку сравнения интегралы и ведут себя одинаково, т.е. оба сходятся. Замечание. При вычислении предела
- 13. §2. Несобственный интеграл II рода (интеграл от разрывной функции) Пусть f(x) непрерывна на промежутке [a, b)
- 14. Если предел в правой части существует, то несобственный интеграл сходится. Если же указанный предел не существует
- 15. Аналогично определяется несобственный интеграл в случае, когда f(x) терпит бесконечный разрыв в точке х = а:
- 16. Пример 4. Вычислить Решение. Подынтегральная функция терпит разрыв в точке с = 0 (точка разрыва 2-го
- 17. Замечание. Если вычислять данный интеграл, не обращая внимание на разрыв подынтегральной функции в точке х =
- 18. Признаки сходимости несобственных интегралов II рода аналогичны признакам сходимости несобственных интегралов I рода. В качестве интеграла,
- 19. Пример 5. Исследовать на сходимость Решение. Подынтегральная функция не определена в точке х = 0. Выясним
- 21. Скачать презентацию
![Тема 2. Несобственные интегралы Определенный интеграл где [a, b] − конечный](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/451450/slide-1.jpg)

![Аналогично определяется несобственный интеграл на промежутке (‒∞, b]: Несобственный интеграл с](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/451450/slide-4.jpg)














 Взаимное расположение прямой и плоскости
Взаимное расположение прямой и плоскости Полиномы над полями конечной характеристики
Полиномы над полями конечной характеристики Матрицы. Определения
Матрицы. Определения Булева алгебра
Булева алгебра Математика в изобразительном искусстве
Математика в изобразительном искусстве Презентация на тему Обозначение натуральных чисел. 5 класс.
Презентация на тему Обозначение натуральных чисел. 5 класс.  Преобразование Фурье
Преобразование Фурье Статистическое наблюдение. Тема 2
Статистическое наблюдение. Тема 2 Круговые диаграммы
Круговые диаграммы Умножение десятичных дробей
Умножение десятичных дробей Декартово произведение
Декартово произведение Признаки равенства треугольников
Признаки равенства треугольников Решение заданий С2
Решение заданий С2 Квадратичная функция и её график
Квадратичная функция и её график Числа Фибоначчи
Числа Фибоначчи Линейная функция. Построение графика функции у= 2х-1
Линейная функция. Построение графика функции у= 2х-1 Типы задач на дроби
Типы задач на дроби Исследование качества школьного математического и естественнонаучного образования TIMSS
Исследование качества школьного математического и естественнонаучного образования TIMSS Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Кластеризация значений пикселей изображений с учетом метрики цветового различия CIEDE-2000
Кластеризация значений пикселей изображений с учетом метрики цветового различия CIEDE-2000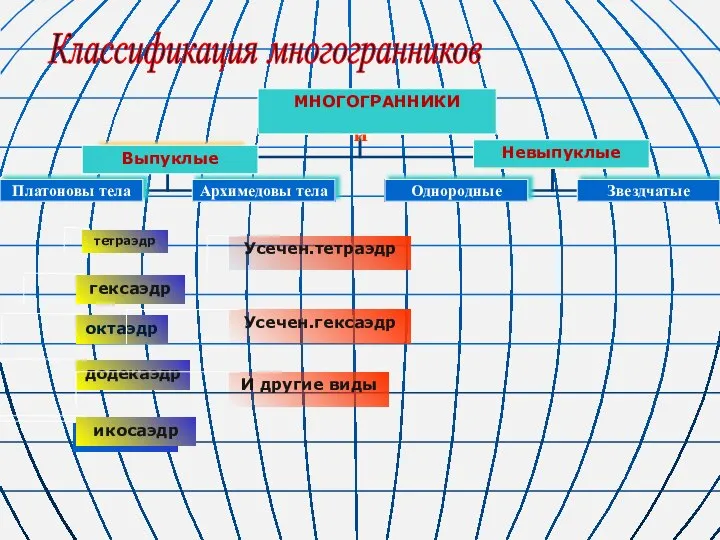 Классификация многогранников
Классификация многогранников Способ подстановки
Способ подстановки 20180306_prezentatsiya
20180306_prezentatsiya Что такое алгебра?
Что такое алгебра? Уравнения прямой и окружности
Уравнения прямой и окружности Длина окружности. Площадь круга
Длина окружности. Площадь круга Правильные многогранники
Правильные многогранники Решение уравнений tgx=a. Понятие арктангенса числа
Решение уравнений tgx=a. Понятие арктангенса числа