Содержание
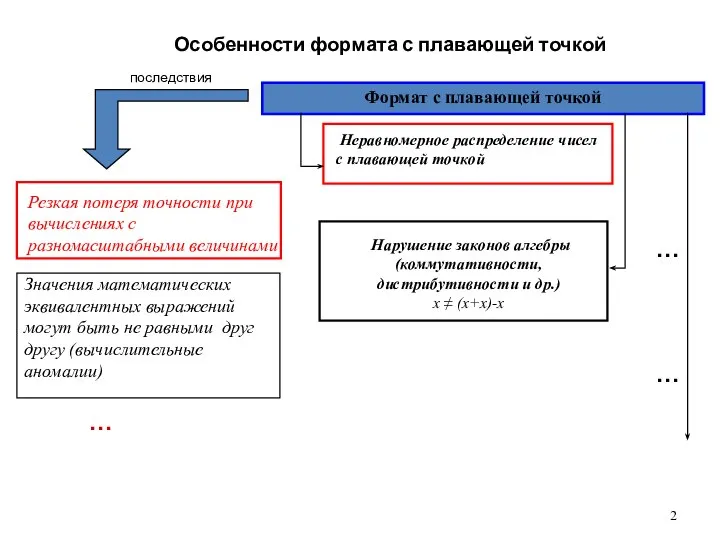
- 2. Особенности формата с плавающей точкой Резкая потеря точности при вычислениях с разномасштабными величинами Неравномерное распределение чисел
- 3. Недостатки формата с плавающей точкой Числа с плавающей точки дают различные результаты на различных аппаратных платформах.
- 4. Нарушение законов алгебры Считаете с одной точностью и с другой если результаты примерно одинаковые, то вероятно
- 5. ПРИМЕР ЗАДАЧИ, ИМЕЮЩЕЙ РЕЗКИЙ РОСТ ОШИБОК ОКРУГЛЕНИЯ Обращение матрицы Гильберта порядка 3 С точностью 2 знака
- 6. Матрица Гильберта Для матрицы 12 уже неверные результаты. Число обусловленности растёт экспоненциально! Некоторые матрицы имеют число
- 7. Модулярная арифметика Амербаев В.М. МОДУЛЯ́РНАЯ АРИФМЕ́ТИКА (система остаточных классов), базируется на известном в теории чисел частном
- 8. Деление с остатком
- 9. Деление с остатком
- 10. Деление с остатком
- 11. Алгоритм Евклида
- 12. Алгоритм Евклида
- 13. Алгоритм Евклида
- 14. Алгоритм Евклида
- 15. Алгоритм Евклида
- 16. ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ
- 17. ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ
- 18. ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ
- 19. Модулярная арифметика с дробями
- 21. Скачать презентацию

















 Презентация по математике "Решение задач" - скачать бесплатно
Презентация по математике "Решение задач" - скачать бесплатно Понятие одночлена. Стандартный вид одночлена
Понятие одночлена. Стандартный вид одночлена Урок математики
Урок математики  Геометрические иллюзии
Геометрические иллюзии Логарифмические неравенства
Логарифмические неравенства Иностранные меры длины
Иностранные меры длины 제1장 통계와 통계학
제1장 통계와 통계학 Логическая задача со спичками
Логическая задача со спичками Машинная арифметика в рациональных числах (лекция 8)
Машинная арифметика в рациональных числах (лекция 8) Основы метрологии
Основы метрологии Презентация по математике "Счёт в 1 классе" - скачать бесплатно
Презентация по математике "Счёт в 1 классе" - скачать бесплатно Квадратные уравнения
Квадратные уравнения История возникновения чисел
История возникновения чисел Состав чисел от 11 до 18. Засели домики (игра-тренажёр) 1 класс
Состав чисел от 11 до 18. Засели домики (игра-тренажёр) 1 класс Ознайомлення з дією множення
Ознайомлення з дією множення Квадратные неравенства. Решение примеров. 9 класс
Квадратные неравенства. Решение примеров. 9 класс Теорема Виета
Теорема Виета Финансовая математика в задачах ЕГЭ и практической деятельности человека
Финансовая математика в задачах ЕГЭ и практической деятельности человека Прямоугольный треугольник. Решение задач
Прямоугольный треугольник. Решение задач Решение задач с помощью систем уравнений (6)
Решение задач с помощью систем уравнений (6) Уравнения - следствия
Уравнения - следствия Четырёхугольники. Сказка - вопрос
Четырёхугольники. Сказка - вопрос Понятия НОД и НОК,
Понятия НОД и НОК, МАТЕМАТИКА
МАТЕМАТИКА  Симметрия в окружающем мире. Симметрия в человеческом творчестве. Орнаменты
Симметрия в окружающем мире. Симметрия в человеческом творчестве. Орнаменты Параллельные прямые
Параллельные прямые Шар. Куб. Параллелепипед.
Шар. Куб. Параллелепипед. Игра "Поле чудес" геометрия
Игра "Поле чудес" геометрия