Содержание
- 2. МЫСЛИТЕЛЬНАЯ ДЕЯТЕЛЬНОСТЬ логика интуиция интуиция-суждение интуиция-догадка «Таким образом, логика и интуиция играют каждая свою необходимую роль.
- 3. λογος (греч.)– слово, смысл Математическая логика: предмет – логика метод – математика Язык: предметный (язык –
- 4. (древнегреч.) Аристотель (384-322 до н.э.): теория дедукции – логического вывода Евклид (330–275 до н.э.) (нем.) Лейбниц
- 5. НАПРАВЛЕНИЯ ОБОСНОВАНИЯ МАТЕМАТИКИ логицизм ((нем.) Фреге(1848-1925), Пирс, (ит.) Пеано (1858-1932), Рассел, (англ.) Уайтхед (1861-1947)) невозможность вывести
- 6. АКСИОМАТИЧЕСКИЙ МЕТОД: 3 СТАДИИ РАЗВИТИЯ
- 7. ЛОГИКА ВЫСКАЗЫВАНИЙ
- 8. ВЫСКАЗЫВАНИЕ Высказывание – исходное понятие (не определяется через другие) Форма существования высказывания – предложение предметного языка,
- 9. ПРОСТЫЕ ВЫСКАЗЫВАНИЯ Примеры: Земля – планета солнечной системы 5×7=35 простые (атомарными, элементарными) истинные высказывания 3×7=22 Рим
- 10. Всякий важный двигатель работает без бензина Земля вращается быстро Который час? Решить квадратное уравнение не высказывания
- 11. СВОБОДНЫЕ И СВЯЗАННЫЕ ВХОЖДЕНИЯ ПЕРЕМЕННОЙ переменная называется связанной, если подстановка в нее имен конкретных объектов недопустима
- 15. А – посылка, антецедент импликации, В – заключение, консеквент ⟷ ⟺ ≡ эквиваленция
- 16. ТАБЛИЦЫ ИСТИННОСТИ СВЯЗОК 0, Л, f, ⏊ 1, И, t, ⏉
- 17. ЛОГИЧЕСКИЕ ОПЕРАЦИИ инверсия, отрицание (НЕ, NOT) конъюнкция (И, AND) дизъюнкция (нестрогая, неисключающая) (ИЛИ, OR) импликация (IMP)
- 18. ПРОПОЗИЦИОНАЛЬНЫЕ ПЕРЕМЕННЫЕ АЛФАВИТ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ Пропозициональные переменные назовем элементарными формулами, или атомами. Алфавит алгебры высказываний: пропозициональные
- 19. ПРОПОЗИЦИОНАЛЬНЫЕ ФОРМУЛЫ А, В – метазнаки (произв. формулы) Формулы в определении: 1) – элементарные (атомы), 2)
- 20. ФОРМАЛИЗАЦИЯ И ИНТЕРПРЕТАЦИЯ Метаязык – это язык, служащий для объяснения другого языка. Формула сама по себе
- 21. КЛАССИФИКАЦИЯ ФОРМУЛ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ выполнимые ( = 1 хотя бы для одной конкретизации) тавтологии (общезначимые, тождественно
- 22. ЛОГИЧЕСКАЯ РАВНОСИЛЬНОСТЬ Два высказывания равносильны, если они одновременно истинны или одновременно ложны. Две формулы равносильны, если
- 23. ПРОВЕРКА ОБЩЕЗНАЧИМОСТИ
- 24. KLEENE ВВЕДЕНИЕ В МЕТАМАТЕМАТИКУ ОСНОВНЫЕ ТАВТОЛОГИИ
- 25. KLEENE ВВЕДЕНИЕ В МЕТАМАТЕМАТИКУ ОСНОВНЫЕ ТАВТОЛОГИИ
- 26. KLEENE ВВЕДЕНИЕ В МЕТАМАТЕМАТИКУ ОСНОВНЫЕ ТАВТОЛОГИИ
- 27. KLEENE ВВЕДЕНИЕ В МЕТАМАТЕМАТИКУ ОСНОВНЫЕ ТАВТОЛОГИИ
- 28. БУЛЕВЫ ФУНКЦИИ Если формула содержит n переменных, то она задает некоторую функцию где = {0, 1}.
- 29. НОРМАЛЬНЫЕ ФОРМЫ ДЛЯ ФОРМУЛ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ Переход к равносильной формуле, содержащей только связки: отрицание конъюнкция дизъюнкция
- 30. НОРМАЛЬНЫЕ ФОРМЫ ДЛЯ ФОРМУЛ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ Дизъюнктивным одночленом от переменных называется дизъюнкция этих переменных или их
- 31. НОРМАЛЬНЫЕ ФОРМЫ ДЛЯ ФОРМУЛ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ Конъюнктивной нормальной формой называется конъюнкция дизъюнктивных одночленов : где -
- 32. СОВЕРШЕННЫЕ НОРМАЛЬНЫЕ ФОРМЫ ДЛЯ ФОРМУЛ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ Одночлен от переменных называется совершенным, если в него от
- 33. СОВЕРШЕННЫЕ НОРМАЛЬНЫЕ ФОРМЫ ДЛЯ ФОРМУЛ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ
- 34. СПОСОБЫ ПРИВЕДЕНИЯ ФОРМУЛЫ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ К СН-ФОРМЕ СДН-форма: СКН-форма:
- 35. СОВЕРШЕННЫЕ НОРМАЛЬНЫЕ ФОРМЫ ДЛЯ ФОРМУЛ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ Теорема (о представлении формул алгебры высказываний совершенными импликативными нормальными
- 36. СПОСОБЫ ПРИВЕДЕНИЯ ФОРМУЛЫ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ К СН-ФОРМЕ СИН-форма:
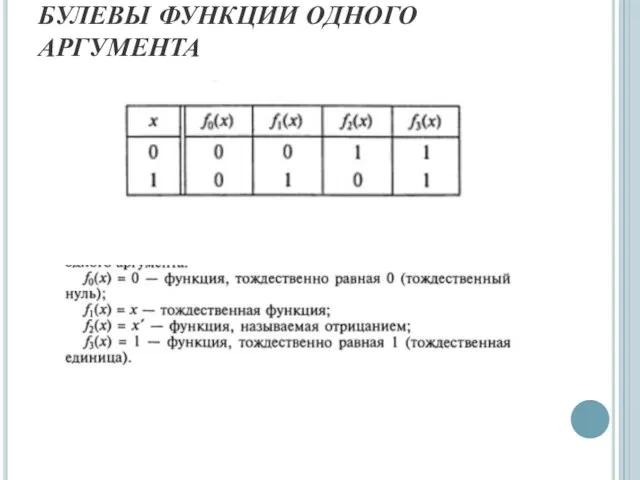
- 37. БУЛЕВЫ ФУНКЦИИ ОДНОГО АРГУМЕНТА
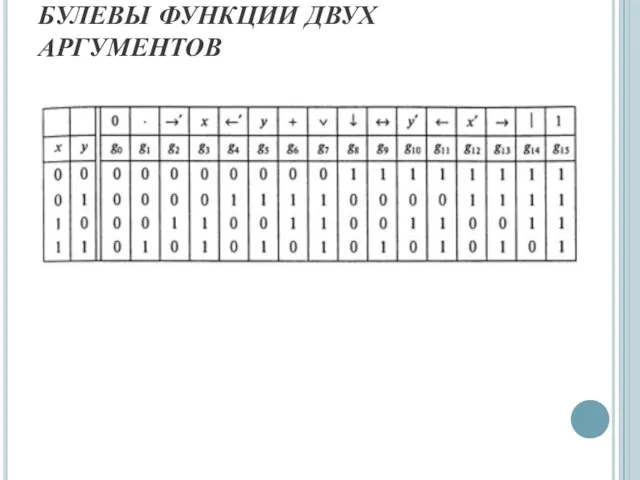
- 38. БУЛЕВЫ ФУНКЦИИ ДВУХ АРГУМЕНТОВ
- 39. БУЛЕВЫ ФУНКЦИИ n АРГУМЕНТОВ
- 40. ЛОГИЧЕСКОЕ СЛЕДСТВИЕ
- 41. ТЕОРЕМА О ДЕДУКЦИИ
- 42. ПРАВИЛА ЛОГИЧЕСКИХ УМОЗАКЛЮЧЕНИЙ (ПРИМЕРЫ СТРУКТУР ПРАВИЛЬНОГО МЫШЛЕНИЯ) Правило вывода:
- 43. ПРАВИЛА ЛОГИЧЕСКИХ УМОЗАКЛЮЧЕНИЙ (ПРИМЕРЫ СТРУКТУР ПРАВИЛЬНОГО МЫШЛЕНИЯ)
- 44. АЛГЕБРА ВЫСКАЗЫВАНИЙ И МАТЕМАТИЧЕСКИЕ ТЕОРЕМЫ Логическая структура - условие, достаточное условие для (для того, чтобы бб
- 45. АЛГЕБРА ВЫСКАЗЫВАНИЙ И МАТЕМАТИЧЕСКИЕ ТЕОРЕМЫ Пусть теорема имеет форму Тогда утверждение называют обратным, - противоположным -
- 46. АЛГЕБРА ВЫСКАЗЫВАНИЙ И МАТЕМАТИЧЕСКИЕ ТЕОРЕМЫ Теорема Тогда противоположное утверждение
- 47. СПОСОБЫ ДОКАЗАТЕЛЬСТВА МАТЕМАТИЧЕСКИХ ТЕОРЕМ косвенного доказательства, доказательства разбором случаев, от противного (приведения к абсурду), цепочкой импликаций,
- 48. ДЕДУКТИВНЫЕ И ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ Умозаключение – переход от посылок к заключению (следствию) (логическая операция, состоящая в
- 49. ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ
- 50. ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ
- 51. ЛОГИКА ПРЕДИКАТОВ
- 52. ПОНЯТИЕ ПРЕДИКАТА
- 53. ПОНЯТИЕ ОДНОМЕСТНОГО ПРЕДИКАТА (ВЫРАЖАЕТ СВОЙСТВО)
- 54. ПРИМЕРЫ ОДНОМЕСТНЫХ ПРЕДИКАТОВ
- 55. ПОНЯТИЕ МНОГОМЕСТНОГО ПРЕДИКАТА (ВЫРАЖАЕТ ОТНОШЕНИЕ)
- 56. КЛАССИФИКАЦИЯ ПРЕДИКАТОВ
- 57. КВАНТОРЫ
- 58. КВАНТОРЫ
- 59. КВАНТОРЫ: ПРИМЕРЫ
- 60. РАВНОСИЛЬНОСТЬ ПРЕДИКАТОВ
- 61. СЛЕДОВАНИЕ ПРЕДИКАТОВ
- 62. РАВНОСИЛЬНЫЕ ФОРМУЛЫ ЛОГИКИ ПРЕДИКАТОВ
- 63. РАВНОСИЛЬНЫЕ ФОРМУЛЫ ЛОГИКИ ПРЕДИКАТОВ
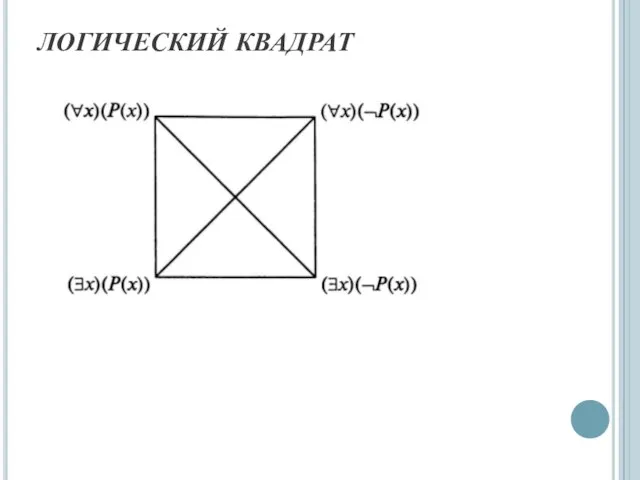
- 64. ЛОГИЧЕСКИЙ КВАДРАТ
- 65. ЛОГИЧЕСКИЙ КВАДРАТ
- 66. ПРИМЕРЫ ОПЕРАТОРОВ, СВЯЗЫВАЮЩИХ ПЕРЕМЕННЫЕ
- 67. ПРИВЕДЕННАЯ ФОРМА
- 68. ПРЕДВАРЕННАЯ НОРМАЛЬНАЯ ФОРМА
- 69. ПРОБЛЕМА РАЗРЕШЕНИЯ ДЛЯ ОБЩЕЗНАЧИМОСТИ И ВЫПОЛНИМОСТИ
- 70. ИСЧИСЛЕНИЯ
- 71. ИСЧИСЛЕНИЕ (ФОРМАЛЬНАЯ ТЕОРИЯ)
- 72. ДОКАЗАТЕЛЬСТВО
- 73. ДОКАЗАТЕЛЬСТВО: ПОЛНОТА ТЕОРИИ
- 74. ДОКАЗАТЕЛЬСТВО: НЕПРОТИВОРЕЧИВОСТЬ
- 75. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
- 76. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
- 77. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
- 78. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
- 79. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
- 80. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ
- 81. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ
- 82. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ
- 83. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ
- 84. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ
- 85. ТЕОРЕМА ГЁДЕЛЯ О НЕПОЛНОТЕ
- 86. ТЕОРЕМА ГЁДЕЛЯ О НЕПОЛНОТЕ
- 87. ТЕОРЕМА ГЁДЕЛЯ О НЕПОЛНОТЕ Логика второго порядка в математической логике – формальная система, расширяющая логику первого
- 88. ЛОГИКА В ШКОЛЬНОЙ МАТЕМАТИКЕ
- 89. ОПРЕДЕЛЕНИЯ: СТРОЕНИЕ Свойство считают существенным для объекта, если оно присуще этому объекту и без него он
- 90. ОПРЕДЕЛЕНИЯ: СТРОЕНИЕ Пример: Объем понятия «прямоугольник» – это множество различных прямоугольников, содержание – свойства прямоугольников: «иметь
- 91. ОПРЕДЕЛЕНИЯ: СТРОЕНИЕ если увеличивается объем понятия, то уменьшается его содержание, и наоборот. Например, объем понятия «квадрат»
- 92. ОПРЕДЕЛЕНИЯ: СТРОЕНИЕ Видовое отличие – это свойства (одно или несколько), которые позволяют выделить определяемые объекты из
- 93. ОПРЕДЕЛЕНИЯ: СТРОЕНИЕ Если понятие а определено через род и видовое отличие, то о его объеме –
- 94. ОПРЕДЕЛЕНИЯ: СТРОЕНИЕ Одно и то же понятие определить через род и видовое отличие, соблюдая сформулированные выше
- 95. ОПРЕДЕЛЕНИЯ: СТРОЕНИЕ Первичные понятия косвенно определяются через систему аксиом математической теории Пример: В элементарной геометрии первичными
- 96. ОПРЕДЕЛЕНИЯ: СТРОЕНИЕ В определении только Q(x) является высказывательной формой Само определение – это соглашение, оно не
- 97. ОПРЕДЕЛЕНИЯ И ТЕОРЕМЫ: СТРОЕНИЕ Внешний квантор общности в определении и теореме часто опускают Квантор существования опускать
- 98. МАТЕМАТИЧЕСКИЕ ПРЕДЛОЖЕНИЯ А(х) => В(х), можно прочитать по разному: Из А(х) следует В(х). Всякое А(х) есть
- 99. МАТЕМАТИЧЕСКИЕ ПРЕДЛОЖЕНИЯ «число х кратно 4» => «число х кратно 2» Всякое число, которое кратно 4,
- 100. МАТЕМАТИЧЕСКИЕ ПРЕДЛОЖЕНИЯ Данное Обратное данному Противоположное данному Контрапозитивное данному (обратное противоположному)
- 101. МАТЕМАТИЧЕСКИЕ ПРЕДЛОЖЕНИЯ Примеры: Дана теорема: «если число делится на 3 и 4, то оно делится на
- 102. МАТЕМАТИЧЕСКИЕ ПРЕДЛОЖЕНИЯ Дана теорема: «во всяком прямоугольнике диагонали равны». Обратное: «если диагонали четырехугольника равны, то он
- 103. ДЕДУКТИВНЫЕ И ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ Умозаключение – переход от посылок к заключению (следствию) (логическая операция, состоящая в
- 104. ДЕДУКТИВНЫЕ И ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ Дедуктивным называется умозаключение, в котором посылки и заключение находятся в отношении логического
- 105. ПРИМЕРЫ СХЕМ ПРАВИЛЬНЫХ УМОЗАКЛЮЧЕНИЙ Правило заключения: Пример: Если запись числа х оканчивается цифрой 5, то число
- 106. ПРИМЕРЫ СХЕМ ПРАВИЛЬНЫХ УМОЗАКЛЮЧЕНИЙ Правило отрицания: Пример: Если запись числа х оканчивается цифрой 5, то число
- 107. ПРИМЕРЫ СХЕМ ПРАВИЛЬНЫХ УМОЗАКЛЮЧЕНИЙ Правило силлогизма: Пример: Если число х кратно 12, то оно кратно 6.
- 108. МАТЕМАТИЧЕСКИЕ РАССУЖДЕНИЯ
- 109. ЛОГИЧЕСКОЕ СЛЕДСТВИЕ
- 110. ДЕДУКТИВНЫЕ И ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ Дедуктивным называется умозаключение, в котором посылки и заключение находятся в отношении логического
- 111. ПРАВИЛЬНЫЕ РАССУЖДЕНИЯ Схема рассуждений называется правильной, если всякое рассуждение по этой схеме, все посылки которого истинны,
- 112. ПРАВИЛЬНЫЕ РАССУЖДЕНИЯ. ПРИМЕР Схема рассуждений правильная?
- 113. ПРАВИЛЬНЫЕ РАССУЖДЕНИЯ. ПРИМЕР Схема рассуждений правильная? В рассуждении посылки истинны, а заключение ложно. Значит, схема неправильная.
- 114. ПРАВИЛЬНЫЕ РАССУЖДЕНИЯ Чтобы доказать, что рассуждение является неправильным, достаточно привести пример рассуждения, имеющего ту же схему,
- 115. БЕСКВАНТОРНЫЕ ПРАВИЛА ДОКАЗАТЕЛЬСТВА - правила удаления конъюнкции - правила введения конъюнкции - правила введения дизъюнкции -
- 116. БЕСКВАНТОРНЫЕ ПРАВИЛА ДОКАЗАТЕЛЬСТВА - правило удаления импликации (modus ponens) - правило силлогизма - правило контрапозиции -
- 117. КВАНТОРНЫЕ ПРАВИЛА ДОКАЗАТЕЛЬСТВА - правило конкретизации - правило доказательства утверждений существования - правило обобщенной контрапозиции
- 118. КВАНТОРНЫЕ ПРАВИЛА ДОКАЗАТЕЛЬСТВА - правило частного заключения - кванторные правила де Моргана
- 119. ФОРМАЛИЗАЦИЯ ДОКАЗАТЕЛЬСТВ В учебниках (школьных, вузовских) доказательства даются как содержательные, поскольку излагаемые в них теории содержательные,
- 120. МЕТОДЫ ДОКАЗАТЕЛЬСТВА Всякое математическое доказательство построено в соответствии с правилами доказательства, т.е. с правильными схемами рассуждений.
- 121. МЕТОДЫ ДОКАЗАТЕЛЬСТВА. ОБОЗНАЧЕНИЯ Предложение в квадратных скобках обозначает допущение. Двойная черта означает, что во вспомогательном рассуждении
- 122. МЕТОД ДОКАЗАТЕЛЬСТВА ПРИВЕДЕНИЕМ К НЕЛЕПОСТИ (REDUCTION AD ABSURDUM) Пусть А – произвольное предложение. Если требуется доказать
- 123. МЕТОД ДОКАЗАТЕЛЬСТВА ОТ ПРОТИВНОГО Пусть А – произвольное предложение. При доказательстве этим методом из допущения не-А
- 124. СПОСОБЫ ДОКАЗАТЕЛЬСТВА МАТЕМ. ТЕОРЕМ косвенного доказательства доказательства разбором случаев, от противного (приведения к абсурду), цепочкой импликаций,
- 125. ЛОГИЧЕСКИЕ ЗАДАЧИ В таких задачах, как правило, имеется ряд высказываний, относительно которых известно, что столько-то из
- 126. ЛОГИЧЕСКИЕ ЗАДАЧИ В нашем примере так как два высказывания истинны, то все дизъюнкции пар высказываний будут
- 127. ЛОГИЧЕСКИЕ ЗАДАЧИ. ЗАДАЧА ПРО ТУРИСТА. Турист направлялся к озеру и дошел до перекрестка, откуда одна дорога
- 128. ЛОГИЧЕСКИЕ ЗАДАЧИ. ЗАДАЧА ПРО ТУРИСТА. Решение. Очевидно, что вопрос должен быть составным высказыванием, в котором одно
- 130. Скачать презентацию




























































































































 Дискретная математика. Часть 4 Элементы математической логики
Дискретная математика. Часть 4 Элементы математической логики Функции многих переменных
Функции многих переменных Решение практико-ориентированных задач
Решение практико-ориентированных задач Подготовка к контрольной работе «Умножение и деление дробей»
Подготовка к контрольной работе «Умножение и деление дробей» Функции, их свойства и графики. Определение функции
Функции, их свойства и графики. Определение функции Решение логарифмических неравенств тип заданий С3
Решение логарифмических неравенств тип заданий С3 Прямоугольные треугольники
Прямоугольные треугольники Экономико-математическое моделирование
Экономико-математическое моделирование Решето Эратосфена Выполнила ученица 6 «Г» класса Алагирова Даяна
Решето Эратосфена Выполнила ученица 6 «Г» класса Алагирова Даяна  Измерение высоты дерева способом «двух товарищей»
Измерение высоты дерева способом «двух товарищей» Равномерное прямолинейное движение. Тест №1
Равномерное прямолинейное движение. Тест №1 Мәдениетінде математика ғылымының дамуы
Мәдениетінде математика ғылымының дамуы Область определения и множество значений тригонометрических функций
Область определения и множество значений тригонометрических функций Развитие математики в России «Стоит только показать, что какая-либо вещь невозможна, как найдется математик, который ее сделает.»
Развитие математики в России «Стоит только показать, что какая-либо вещь невозможна, как найдется математик, который ее сделает.» Конденсацияланған қатты денелердің құрылымы
Конденсацияланған қатты денелердің құрылымы Коэффициенты квадратного уравнения
Коэффициенты квадратного уравнения Симметрии в технике
Симметрии в технике Чётные и нечётные функции
Чётные и нечётные функции Неравенства второй степени с одной переменной
Неравенства второй степени с одной переменной Памятка по математике языку для 1 класса
Памятка по математике языку для 1 класса Арифметические функции. (Лекция 10)
Арифметические функции. (Лекция 10) Решение расчетных задач при подготовке учащихся к сдачи ЕГЭ
Решение расчетных задач при подготовке учащихся к сдачи ЕГЭ Презентация по математике "Набор из 4-х тестов по подготовке к ОГЭ математика" - скачать бесплатно
Презентация по математике "Набор из 4-х тестов по подготовке к ОГЭ математика" - скачать бесплатно Неравенство треугольника
Неравенство треугольника Отношения и пропорции
Отношения и пропорции Тема урока: «Числа от 1 до 100. Письменные вычисления»
Тема урока: «Числа от 1 до 100. Письменные вычисления»  Коэффициент корреляции и корреляционный анализ
Коэффициент корреляции и корреляционный анализ В мире необыкновенных животных
В мире необыкновенных животных