Содержание
- 2. Мат. статистика – наука о принятии решений в условиях неопределенности. ЗАДАЧА МАТ.СТАТИСТИКИ состоит в создании методов
- 3. Санитарная (медицинская) статистика широко используется при изучении вопросов, связанных с медициной, гигиеной и здравоохранением. Основные разделы:
- 4. Выявление особенностей в состоянии здоровья населения и факторов, определяющих его; 2. Изучение данных о сети, деятельности
- 5. Статистическая совокупность, ее элементы и признаки Статистическая совокупность – это группа, состоящая из большого числа относительно
- 6. Каждая единица наблюдения имеет много характеристик, однако учитываются только те из них, которые необходимы для достижения
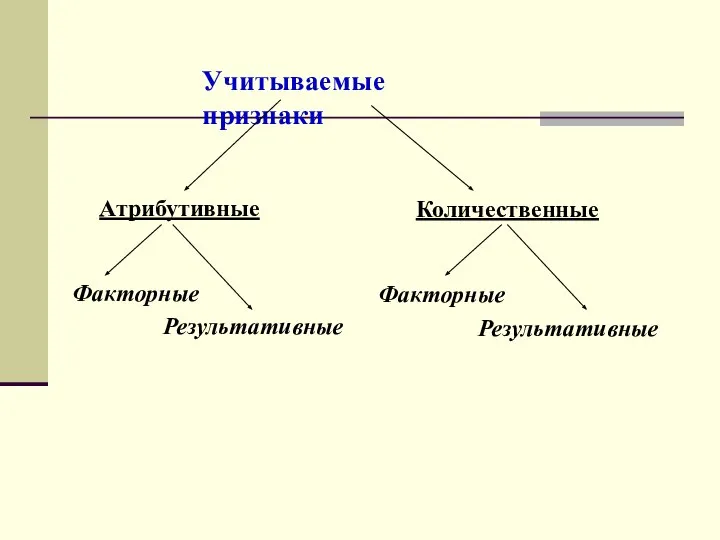
- 7. Учитываемые признаки делятся (по характеру) Пол, профессия, место жительства, исходы лечения и т.д. а) атрибутивные (описательные)
- 8. Учитываемые признаки Атрибутивные Количественные Факторные Результативные Факторные Результативные
- 9. Факторными называются такие учитываемые признаки, под влиянием которых изменяются другие, зависящие от них результативные признаки. С
- 10. Факторные признаки: методы профилактики и лечения (или доза лекарств), пол, возраст, профессия, образование, доход. Результативные признаки:
- 11. Каждая статистическая совокупность может рассматриваться как генеральная или как выборочная, от этого зависит интерпретация результатов исследования.
- 12. Выборочная совокупность – часть генеральной совокупности, отобранная специальным методом и предназначенная для характеристики генеральной совокупности.
- 13. Выборочная совокупность – часть генеральной совокупности Генеральная совокупность – совокупность всех исследуемых объектов Выборочный метод –
- 14. Основные показатели выборки: Вариант Объем Размах Частота Относительная частота
- 15. Вариант количественное значение элемента выборки. Обозначается - Х
- 16. Объем выборки число объектов выборки Обозначается - n Например: Если из 300 студентов, для контрольной флюорографии
- 17. Размах выборки разность между наибольшим и наименьшим значениями числовой выборки. Обозначается - W
- 18. Частота значения выборки Количество данного варианта в выборке. Обозначается – ni Условие:
- 19. Относительные частоты значений выборки Это отношения вида Обозначаются: pi Условие:
- 20. Вариационный ряд Это неубывающая числовая последовательность
- 21. Статистический ряд Последовательность пар или троек чисел Статистический ряд обычно записывают в виде таблицы:
- 22. Для оценки изучаемых явлений, составляющих статистическую совокупность, используют статистические величины – абсолютные числа, относительные и средние
- 23. Наиболее часто используют следующие относительные величины (показатели): Интенсивный показатель = абс. размер явления*100(1000, 10 000, 100
- 25. Скачать презентацию





















 Арифметическая прогрессия
Арифметическая прогрессия Применение распределительного свойства умножения. 6 класс
Применение распределительного свойства умножения. 6 класс Презентация по математике "Кто хочет стать математиком?" - скачать бесплатно
Презентация по математике "Кто хочет стать математиком?" - скачать бесплатно Умножение вектора на число
Умножение вектора на число Аттестационная работа. Решение текстовых задач Элективный курс по математике для 9 класса
Аттестационная работа. Решение текстовых задач Элективный курс по математике для 9 класса Коэффициент. Приведение подобных слагаемых. 6 класс
Коэффициент. Приведение подобных слагаемых. 6 класс Иллюзии и математические парадоксы
Иллюзии и математические парадоксы Арифметическая прогрессия. Тест
Арифметическая прогрессия. Тест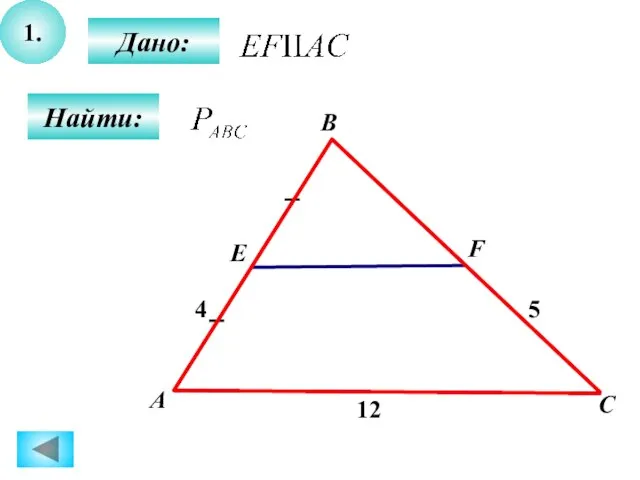 Задачи на повторение
Задачи на повторение Решение задач по теме: «Подобие треугольников»
Решение задач по теме: «Подобие треугольников» Основные типы и виды шкал. Шкалирование
Основные типы и виды шкал. Шкалирование Масштаб. 6 класс
Масштаб. 6 класс Свойства корней степени n
Свойства корней степени n Презентация по математике "Многогранники. Призма" - скачать бесплатно
Презентация по математике "Многогранники. Призма" - скачать бесплатно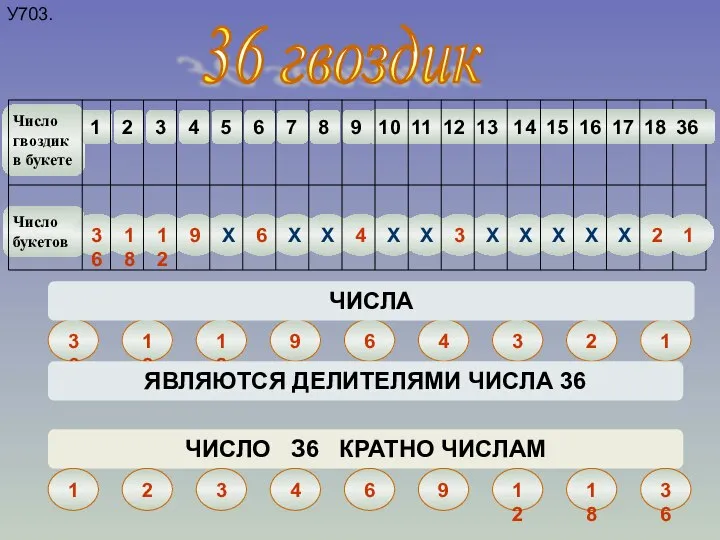 Делители и кратные
Делители и кратные Логические операции с понятиями
Логические операции с понятиями Площадь многоугольников
Площадь многоугольников Задача з піцою
Задача з піцою Решение заданий В7 тригонометрия по материалам открытого банка задач ЕГЭ
Решение заданий В7 тригонометрия по материалам открытого банка задач ЕГЭ Регрессионный анализ
Регрессионный анализ Проценты. Устная работа
Проценты. Устная работа Секреты таблицы умножения
Секреты таблицы умножения Средняя линия (8 класс)
Средняя линия (8 класс) Геометрия вокруг нас
Геометрия вокруг нас Graphs and Multigraphs
Graphs and Multigraphs Двоичная система счисления (10 класс)
Двоичная система счисления (10 класс) Умножение десятичных дробей
Умножение десятичных дробей Нам радостно, нам весело! Смеемся мы с утра. Но вот пришло мгновенье, Серьезным быть пора. Глазки прикрыли, ручки сложили, Головки
Нам радостно, нам весело! Смеемся мы с утра. Но вот пришло мгновенье, Серьезным быть пора. Глазки прикрыли, ручки сложили, Головки