Содержание
- 2. Оглавление (для перехода к соответствующему разделу нажмите кнопку) Введение Понятие генеральной совокупности и выборки Измерения и
- 3. Исследование в любой области, в том числе и в педагогике, психологии, социологии, предполагает получение результатов -
- 4. Но любая программа обработки данных переводит один набор чисел в другой набор чисел. При этом предлагается
- 5. Эти умения не заменят ни компьютерная программа, ни математик и программист, придумавшие и написавшие данную программу.
- 6. Единое информационное пространство ЧЕЛОВЕКОВЕДЕНИЕ ПЕДАГОГИКА ПСИХОЛОГИЯ СОЦИОЛОГИЯ Педагогическая Психология Социальная психология Социальная педагогика
- 7. Основные вопросы, на которые нужно уметь отвечать специалисту (любому!) ЭТО И ЕСТЬ ОСНОВЫ СИСТЕМНО-СТРУКТУРНОГО АНАЛИЗА
- 8. Основные задачи, которые стоят перед специалистом ОСНОВНОЕ: ФОРМИРОВАНИЕ ПРОФЕССИОНАЛЬНЫХ КОМПЕТЕНЦИЙ
- 9. Соотношение обыденного и научного познания
- 10. Генеральная совокупность и выборка В дальнейшем мы будем исходить из следующих положений: Генеральная совокупность — это
- 11. Репрезентативность выборки — иными словами, ее представительность - это способность выборки представлять изучаемые явления достаточно полно
- 12. Статистическая достоверность, или статистическая значимость, результатов исследования определяется при помощи методов статистического вывода которые предъявляют определенные
- 13. ИЗМЕРЕНИЯ И ШКАЛЫ Измерение в терминах производимых исследователем операций - это приписывание объекту числа по определенному
- 14. 3. В шкале интервалов, или интервальной шкале, каждое из возможных значений измеренных величин отстоит от ближайшего
- 15. ФОРМЫ УЧЕТА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ Исходная информация может быть представлена в виде: Таблиц; Числовых последовательностей; Статистических рядов;
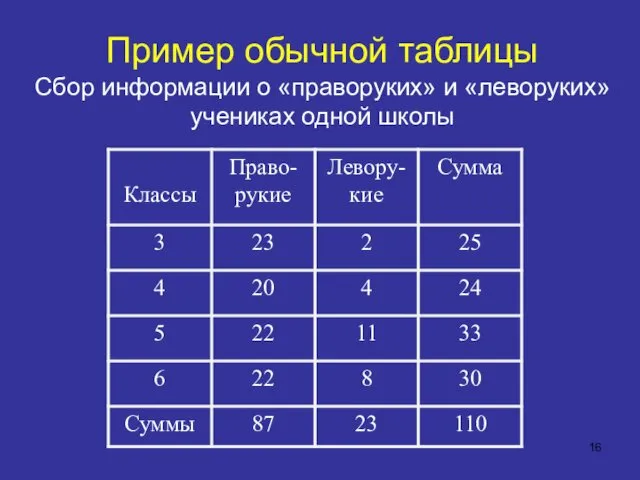
- 16. Пример обычной таблицы Сбор информации о «праворуких» и «леворуких» учениках одной школы
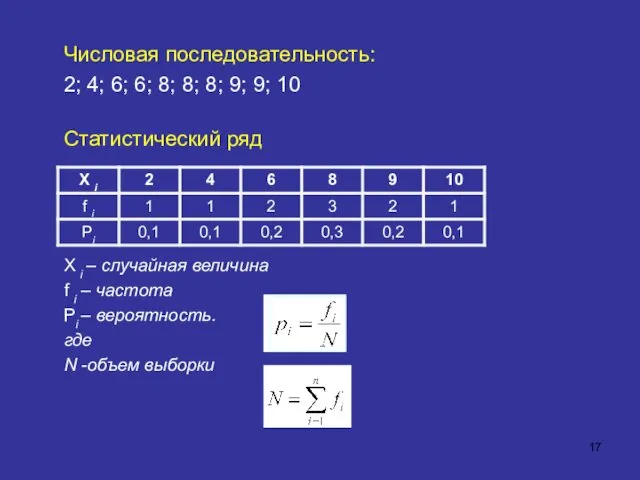
- 17. Числовая последовательность: 2; 4; 6; 6; 8; 8; 8; 9; 9; 10 Статистический ряд X i
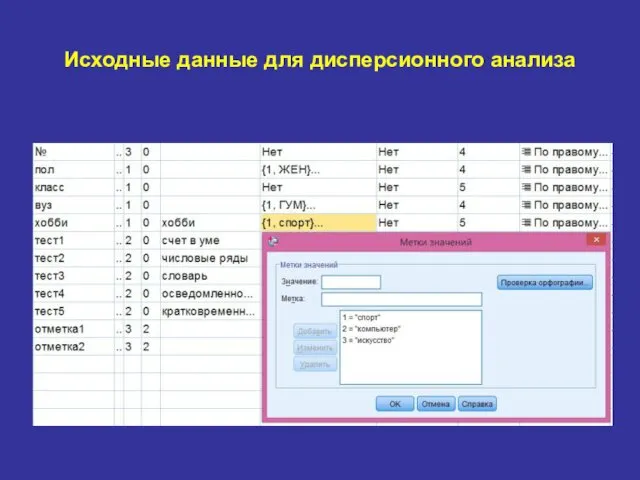
- 18. Пример формирования имени признака, метки и её значений с помощью SPSS (Statistical Package for the Social
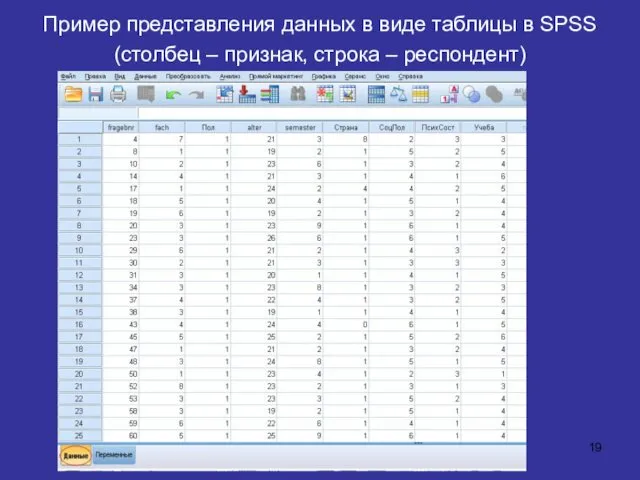
- 19. Пример представления данных в виде таблицы в SPSS (столбец – признак, строка – респондент)
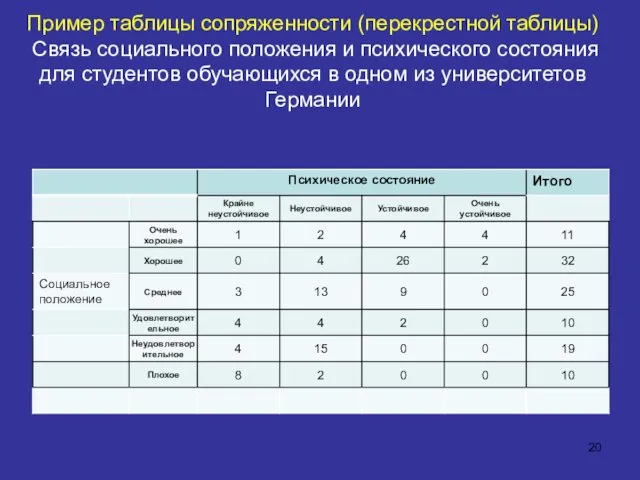
- 20. Пример таблицы сопряженности (перекрестной таблицы) Связь социального положения и психического состояния для студентов обучающихся в одном
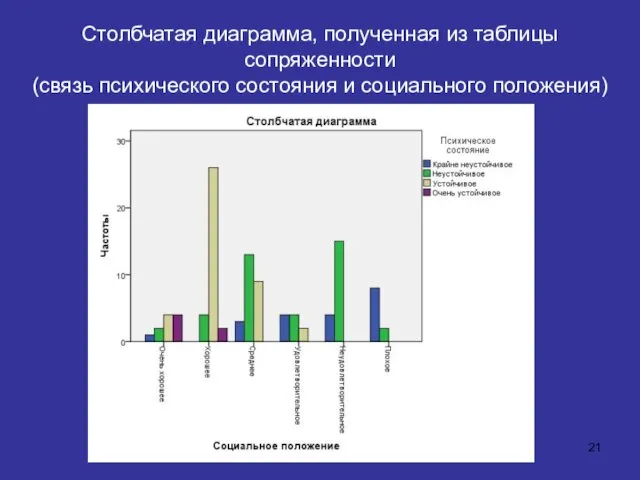
- 21. Столбчатая диаграмма, полученная из таблицы сопряженности (связь психического состояния и социального положения)
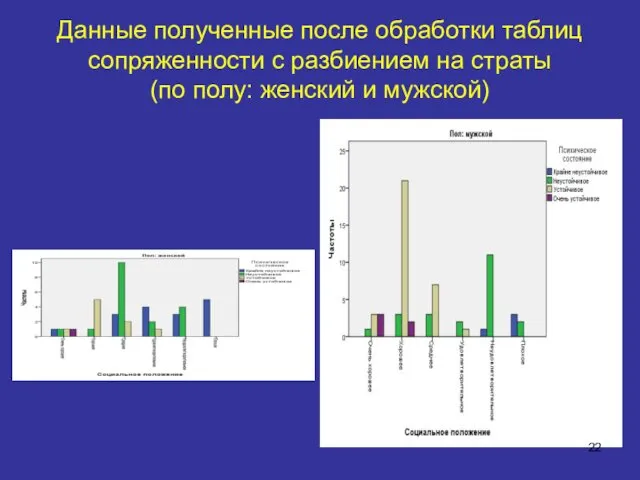
- 22. Данные полученные после обработки таблиц сопряженности с разбиением на страты (по полу: женский и мужской)
- 23. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ РАСПРЕДЕЛЕНИЙ. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ Числовой характеристикой выборки как правило не требующей вычислений является так называемая
- 24. Квантиль - это точка на числовой прямой, которая делит совокупность исходных наблюдений на две части с
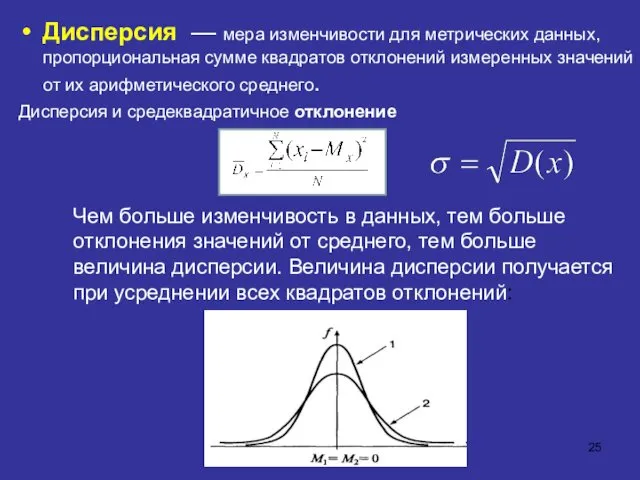
- 25. Дисперсия — мера изменчивости для метрических данных, пропорциональная сумме квадратов отклонений измеренных значений от их арифметического
- 26. Нормальное распределение играет большую роль в математической статистике, поскольку многие статистические методы предполагают, что, анализируемые с
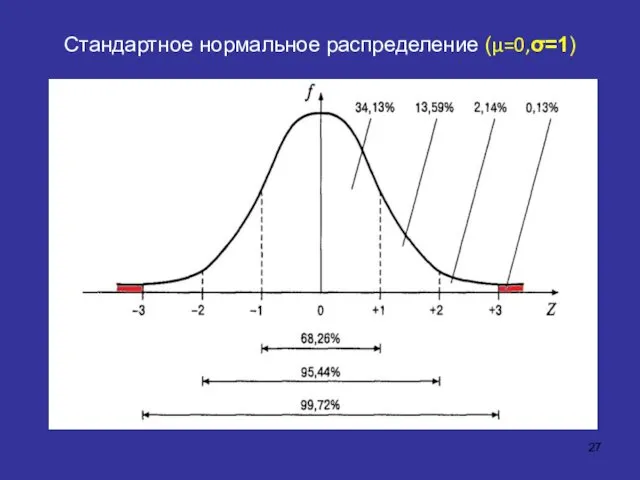
- 27. Стандартное нормальное распределение (μ=0,σ=1)
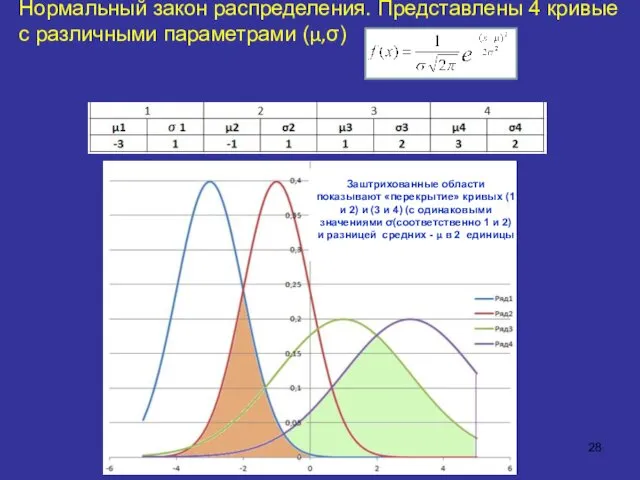
- 28. Нормальный закон распределения. Представлены 4 кривые с различными параметрами (μ,σ) Заштрихованные области показывают «перекрытие» кривых (1
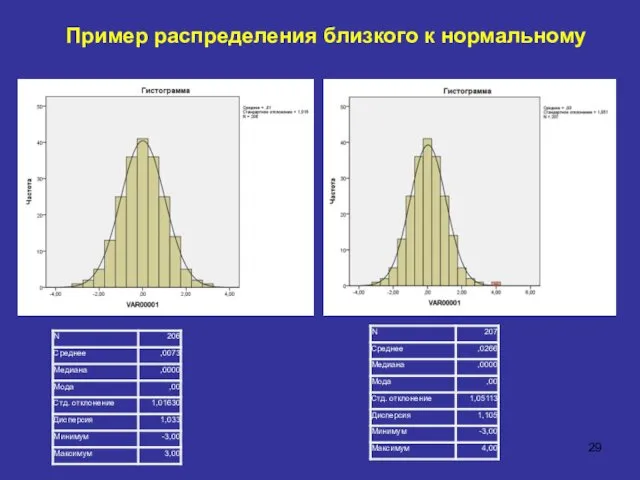
- 29. Пример распределения близкого к нормальному
- 30. Для отражения близости формы распределения к нормальному виду существует две основные характеристики: асимметрия и эксцесс. Эксцесс
- 31. Асимметрия (skewness) показывает, в какую сторону относительно среднего сдвинуто большинство значений распределения. Нулевое значение асимметрии означает
- 32. Асимметрия – это показатель симметричности / скошенности кривой распределения, а эксцесс определяет ее островершинность. При левостронней
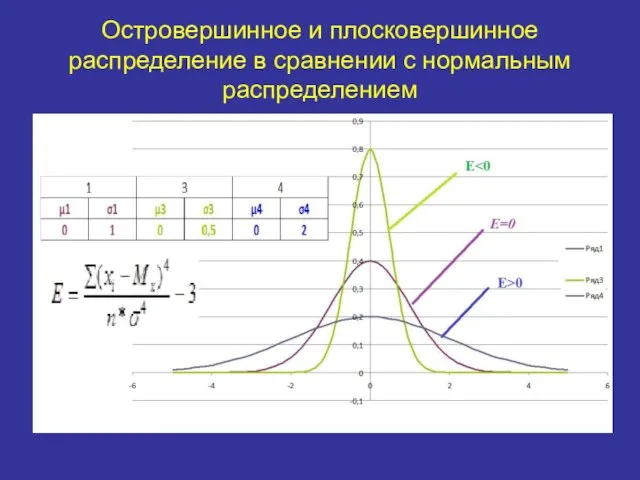
- 33. Если в распределении преобладают значения близкие к среднему арифметическому, то формируется островершинное распределение. В этом случае
- 34. Распределение оценивается как предположительно близкое к нормальному, если установлено, что от 50 до 80 % всех
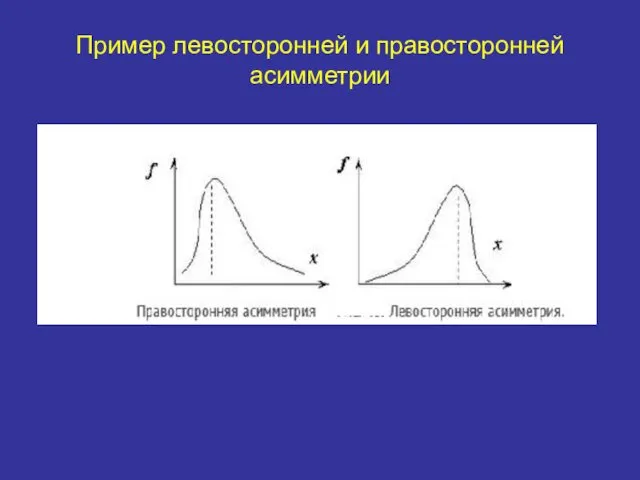
- 35. Пример левосторонней и правосторонней асимметрии
- 36. Островершинное и плосковершинное распределение в сравнении с нормальным распределением
- 37. ОБЩИЕ ПРИНЦИПЫ ПРОВЕРКИ СТАТИСТИЧЕСКИХ ГИПОТЕЗ Под статистической гипотезой обычно понимают формальное предположение о том, что сходство
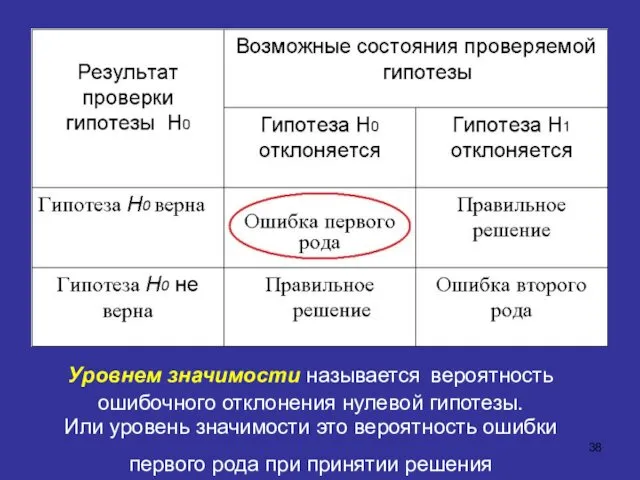
- 38. Уровнем значимости называется вероятность ошибочного отклонения нулевой гипотезы. Или уровень значимости это вероятность ошибки первого рода
- 39. Традиционная интерпретация уровней значимости при α=0.05
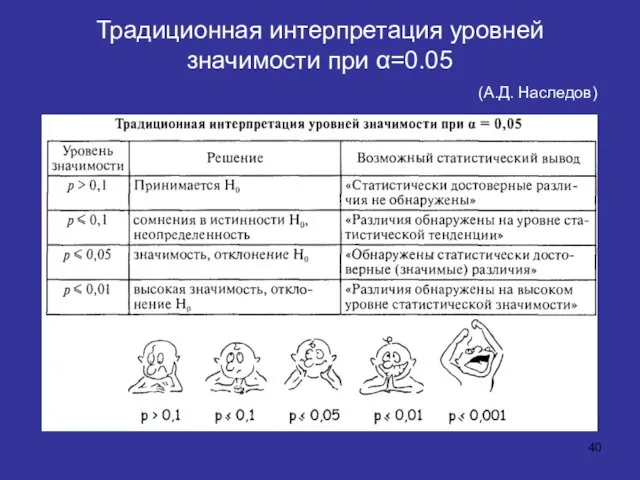
- 40. Традиционная интерпретация уровней значимости при α=0.05 (А.Д. Наследов)
- 41. Из приведенного ниже слайда следует, что точка на оси значимости отражает положение полученного результата относительно двух
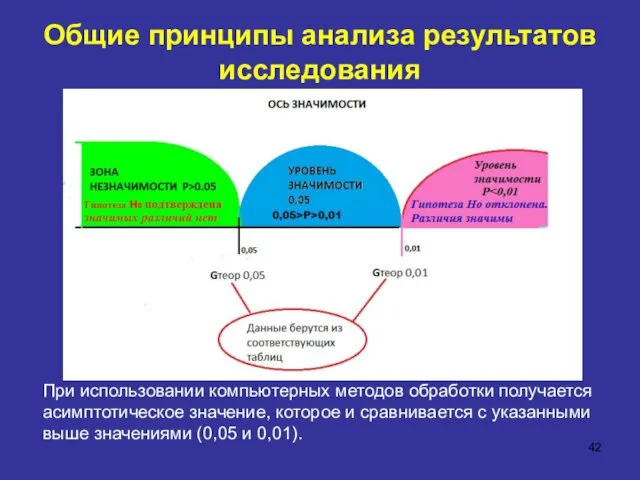
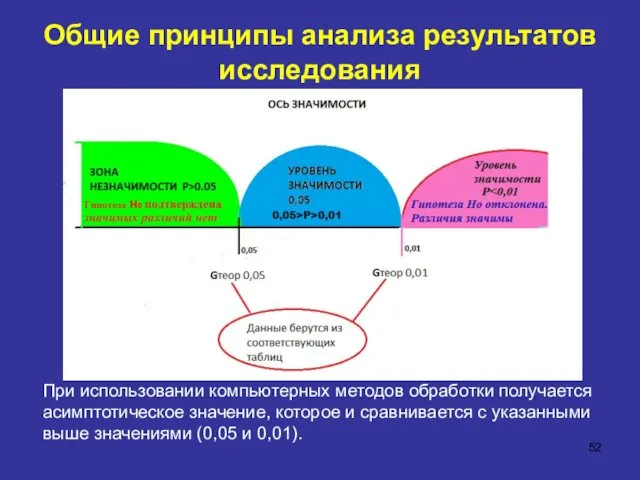
- 42. Общие принципы анализа результатов исследования При использовании компьютерных методов обработки получается асимптотическое значение, которое и сравнивается
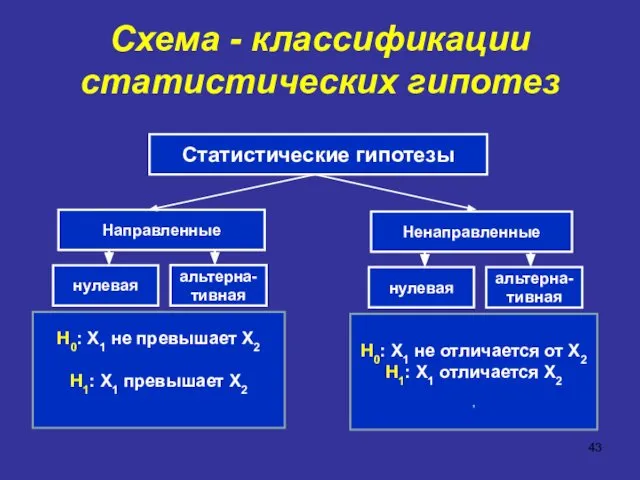
- 43. Схема - классификации статистических гипотез Статистические гипотезы Направленные нулевая Ненаправленные альтерна- тивная нулевая альтерна- тивная Н0:
- 44. Классификация задач, решаемых с использованием математических методов Задачи, требующие установления сходства или различия. Задачи, требующие группировки
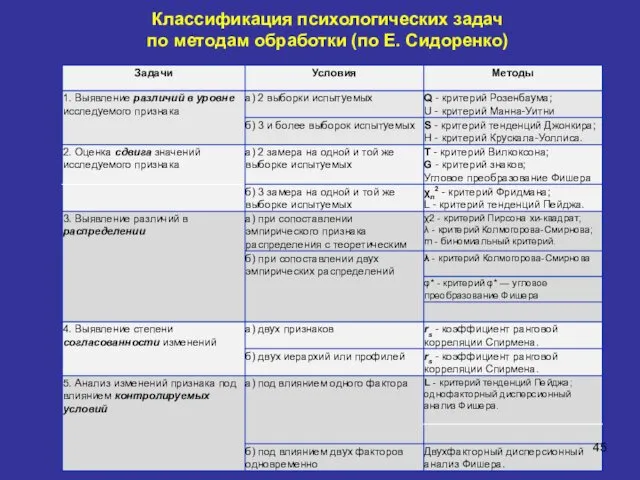
- 45. Классификация психологических задач по методам обработки (по Е. Сидоренко)
- 46. Дополнительные возможности
- 47. СТАТИСТИЧЕСКИЕ КРИТЕРИИ
- 48. Параметрические критерии Критерии, включающие в формулу расчета параметры распределения, то есть средние и дисперсии (t-критерий Стьюдента,
- 49. ПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ Позволяют прямо оценить различия в средних, полученных в двух выборках (t - критерий Стьюдента).
- 50. НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ 1. Позволяют оценить лишь средние тенденции, например, ответить на вопрос, чаще ли в выборке
- 51. 4. Экспериментальные данные могут не отвечать ни одному из этих условий: а) значения признака могут быть
- 52. Общие принципы анализа результатов исследования При использовании компьютерных методов обработки получается асимптотическое значение, которое и сравнивается
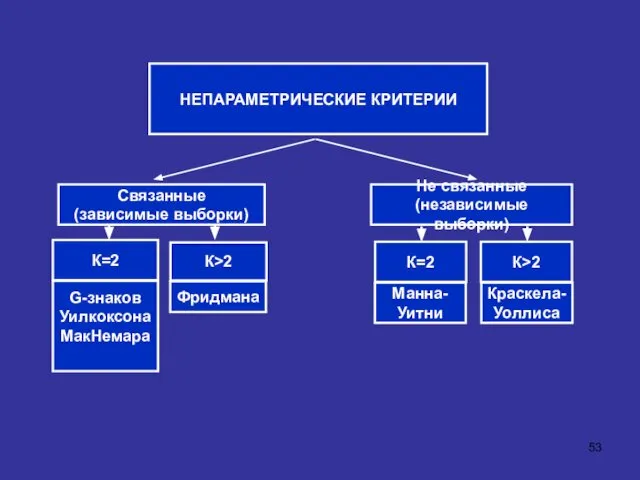
- 53. НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ Связанные (зависимые выборки) К=2 Не связанные (независимые выборки) К>2 К=2 К>2 G-знаков Уилкоксона МакНемара
- 54. G - Критерий знаков Критерий знаков используется при проверке нулевой гипотезы о равенстве двух непрерывно распределенных
- 55. Критерий Мак-Немара - является аналогом непараметрического критерия Уилкоксона, применяется для анализа связанных измерений в случае изменения
- 56. Критерий Фридмана - это непараметрический аналог дисперсионного анализа повторных измерений, применяется для анализа повторных измерений, связанных
- 57. U-критерий Манна — Уитни Непараметрический критерий, используемый для оценки различий между двумя независимыми выборками по уровню
- 58. Н - критерий Крускала-Уоллиса. Критерий предназначен для оценки различий одновременно между тремя, четырьмя и т.д. выборками
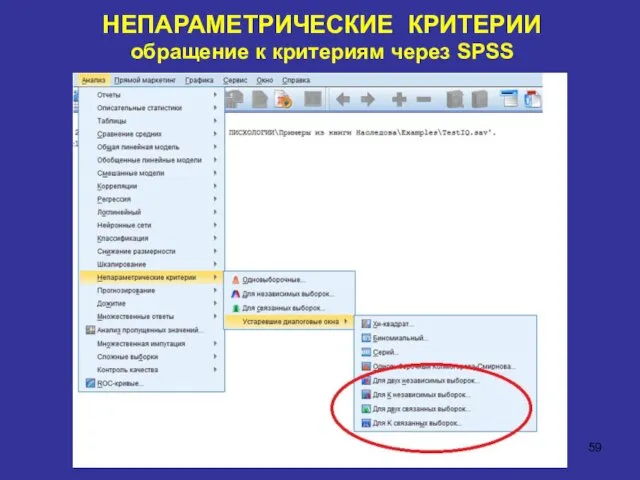
- 59. НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ обращение к критериям через SPSS
- 60. SPSS Критерий Вилкоксона
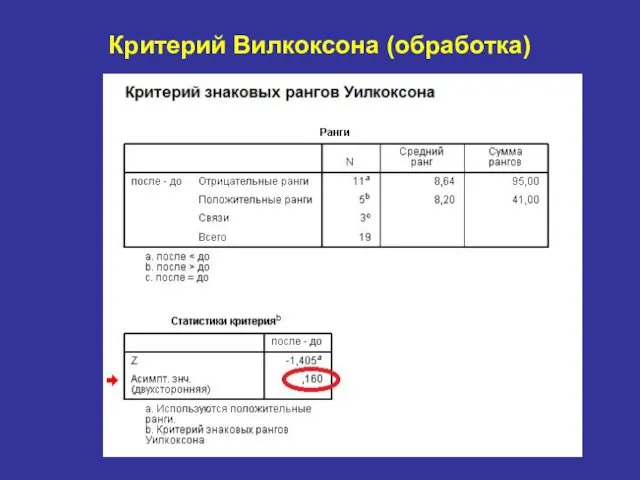
- 61. Критерий Вилкоксона (обработка)
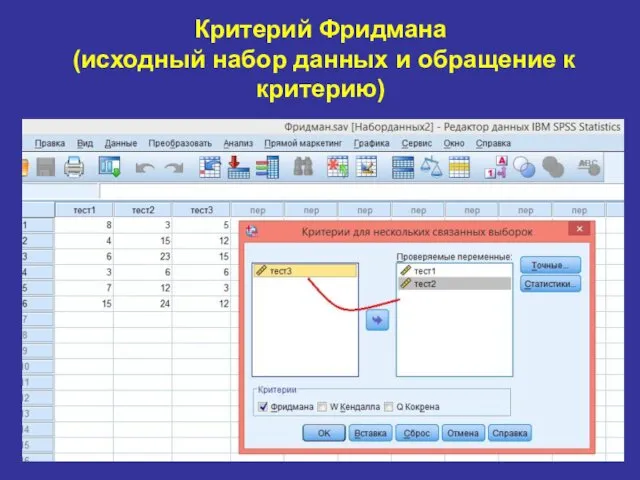
- 62. Критерий Фридмана (исходный набор данных и обращение к критерию)
- 63. Результат обработки Нулевая гипотеза подтверждена
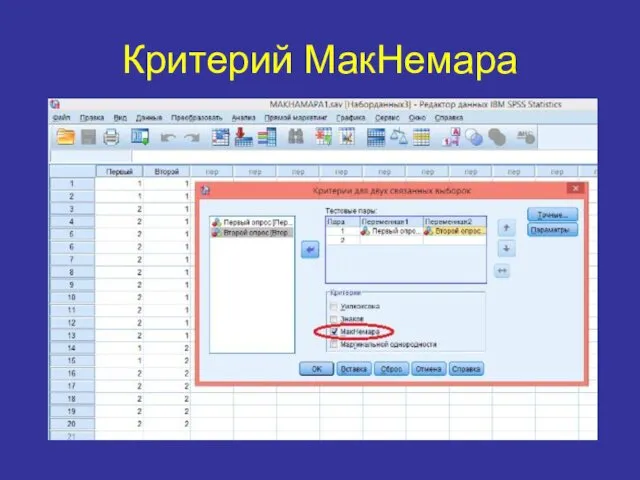
- 64. Критерий МакНемара
- 65. Различия на уровне значимости 0,05
- 66. Критерий Манна Уитни Сравнение результатов контрольной работы двух классов. Данные ранжированы
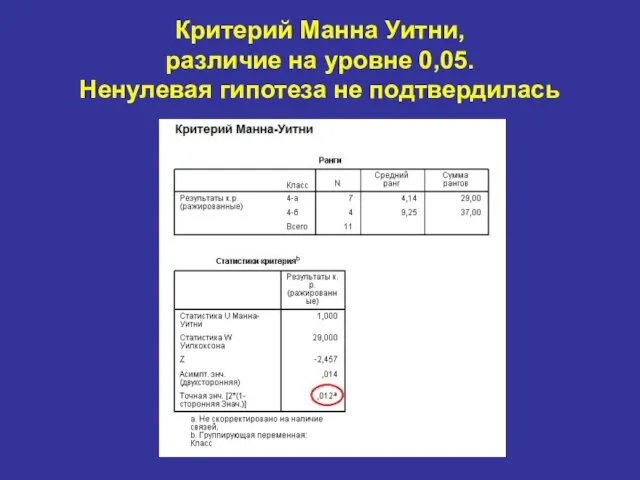
- 67. Критерий Манна Уитни, различие на уровне 0,05. Ненулевая гипотеза не подтвердилась
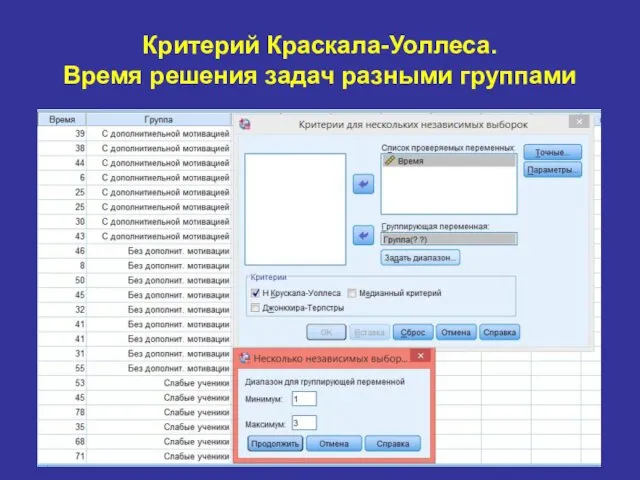
- 68. Критерий Краскала-Уоллеса. Время решения задач разными группами
- 69. Обработка критерия
- 71. Т-критерий Стьюдента Критерий t Стьюдента направлен на оценку различий величин средних и двух выборок X и
- 72. В случае неравночисленных выборок , выражение будет вычисляться следующим образом: В обоих случаях подсчет числа степеней
- 73. Различные варианты обработки данных с применением t -критерия позволяют сделать вывод о различии двух средних значений.
- 74. T-критерий для независимых выборок предназначен для сравнения средних значений двух выборок. Для сравниваемых выборок должны быть
- 75. T-критерий для парных, или зависимых, выборок позволяет сравнить средние значения двух измерений одного признака для одной
- 76. Одновыборочный t-критерий позволяет сравнить среднее значение этой выборки с некоторой эталонной величиной. Например, отличается ли среднее
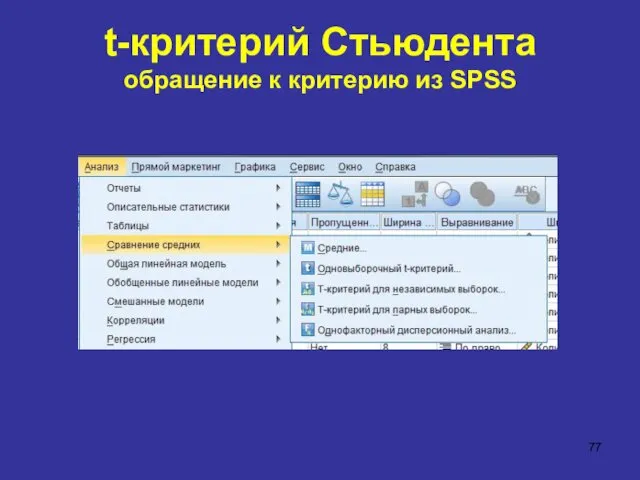
- 77. t-критерий Стьюдента обращение к критерию из SPSS
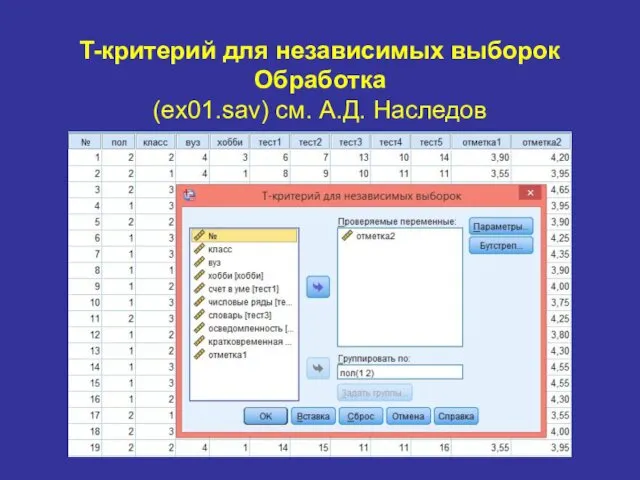
- 78. T-критерий для независимых выборок Обработка (ex01.sav) см. А.Д. Наследов
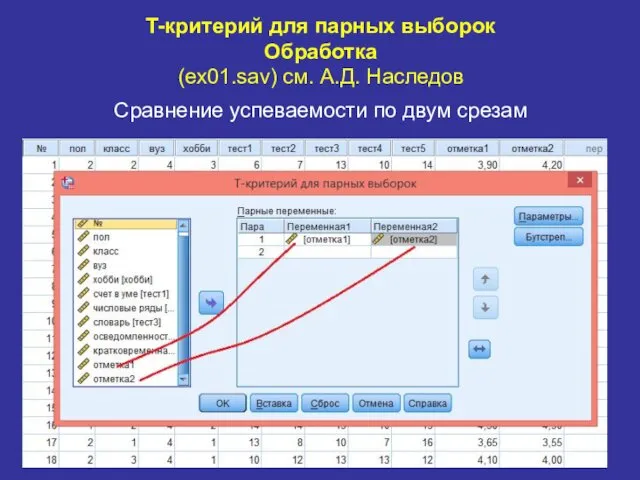
- 80. T-критерий для парных выборок Обработка (ex01.sav) см. А.Д. Наследов Сравнение успеваемости по двум срезам
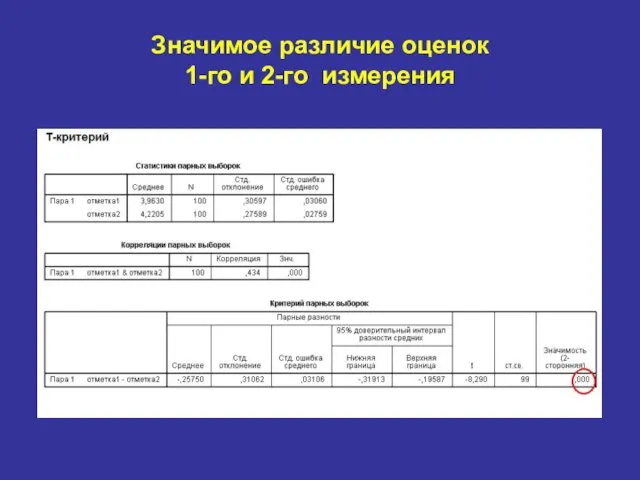
- 82. Значимое различие оценок 1-го и 2-го измерения
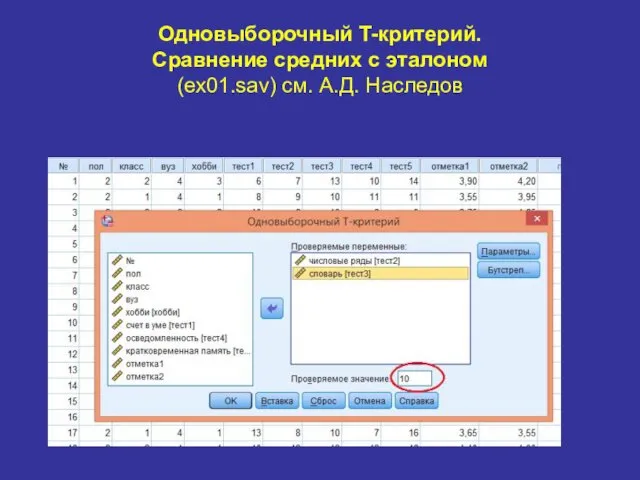
- 83. Одновыборочный T-критерий. Сравнение средних с эталоном (ex01.sav) см. А.Д. Наследов
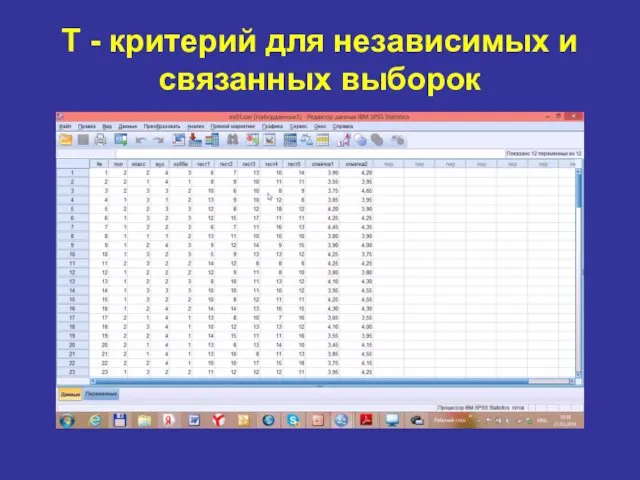
- 86. T - критерий для независимых и связанных выборок
- 87. Дисперсионный анализ Дисперсионный анализ (Analysis Of Variances, ANOVA — общепринятое обозначение метода) — это процедура сравнения
- 88. Ближайшим и более простым аналогом ANOVA является t-критерий. В отличие от t-критерия дисперсионный анализ предназначен для
- 89. Вариативность, обусловленная действием исследуемых переменных и их взаимодействием соотносится со случайной вариативностью. Показателем этого соотношения является
- 90. Например, если мы выдвигаем гипотезу о зависимости успешности работы должностного лица от фактора Н (социальной смелости
- 91. Исходные данные для дисперсионного анализа
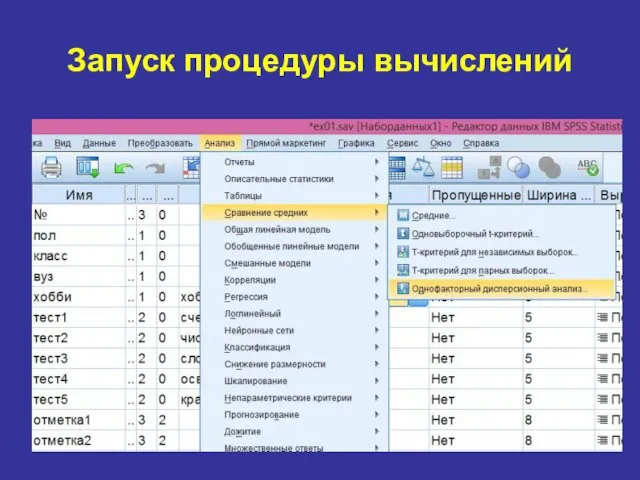
- 92. Запуск процедуры вычислений
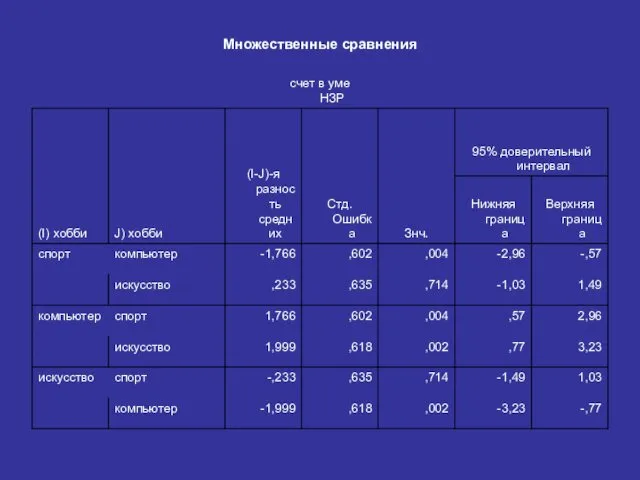
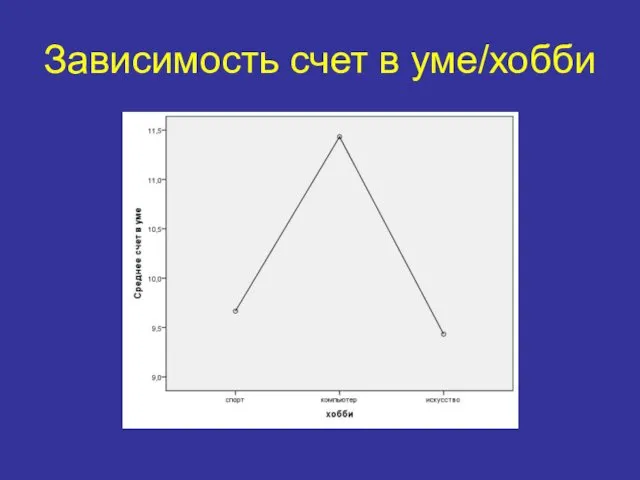
- 97. Зависимость счет в уме/хобби
- 99. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ Корреляция - это статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно
- 100. Использование коэффициентов корреляции в зависимости от типа шкалы измерения
- 101. Корреляция Пирсона, называемся так же линейной корреляцией. Установить прямую связь между переменными и их абсолютными значениями
- 102. Формула для вычисления коэффициента корреляции Пирсона В случае двух переменных коэффициент корреляции вычисляется по следующей формуле:
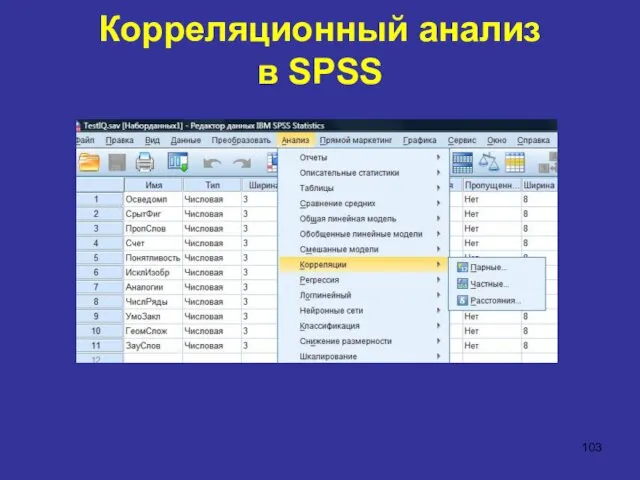
- 103. Корреляционный анализ в SPSS
- 104. Запуск программы вычисления
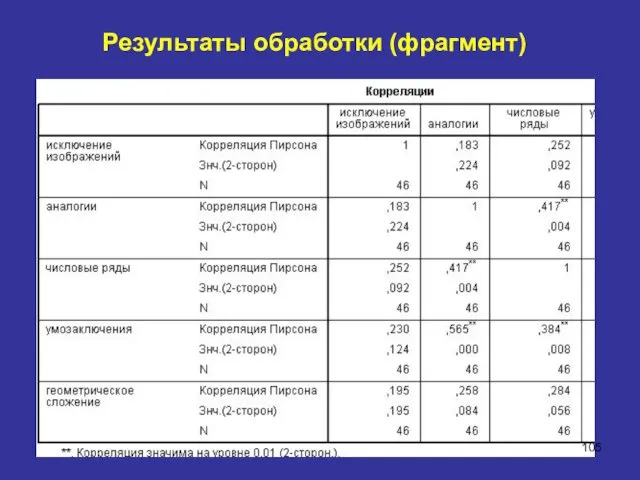
- 105. Результаты обработки (фрагмент)
- 106. Коэффициентом ранговой корреляции Спирмена называют непараметрический метод, используемый при статистическом исследовании связи между различными явлениями. Два
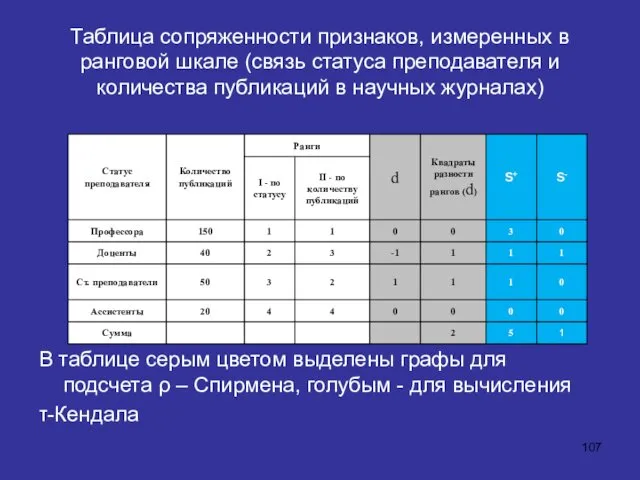
- 107. Таблица сопряженности признаков, измеренных в ранговой шкале (связь статуса преподавателя и количества публикаций в научных журналах)
- 108. Коэффициент корреляции Спирмена Пример вычисления где: di разность пар рангов для i-го объекта, n – число
- 109. Для вычисления коэффициента ранговой корреляции Кендала выделим пару объектов и сравним их ранги по одному признаку
- 110. Коэффициент корреляции Кендала Пример вычисления Где берутся из таблицы сопряженности
- 111. gh
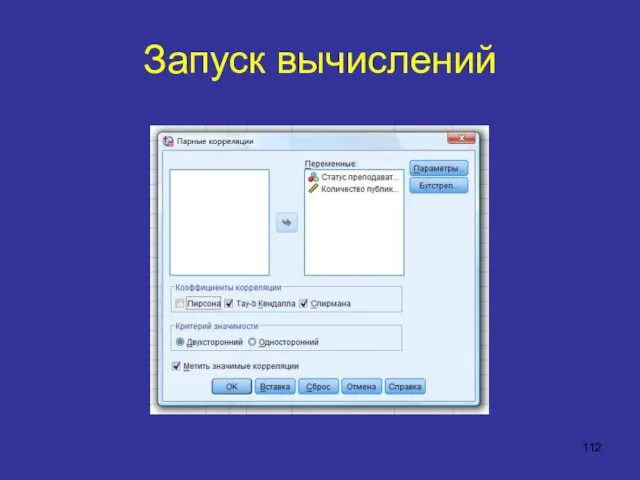
- 112. Запуск вычислений
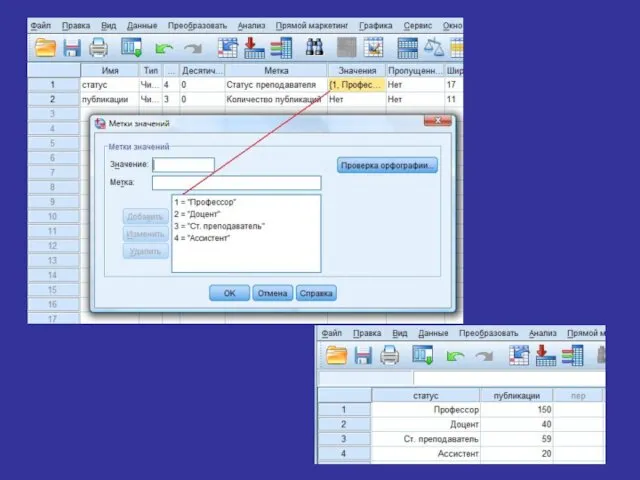
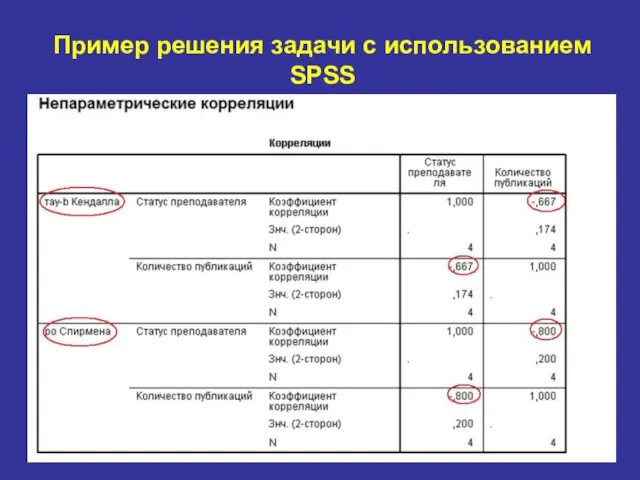
- 113. Пример решения задачи с использованием SPSS
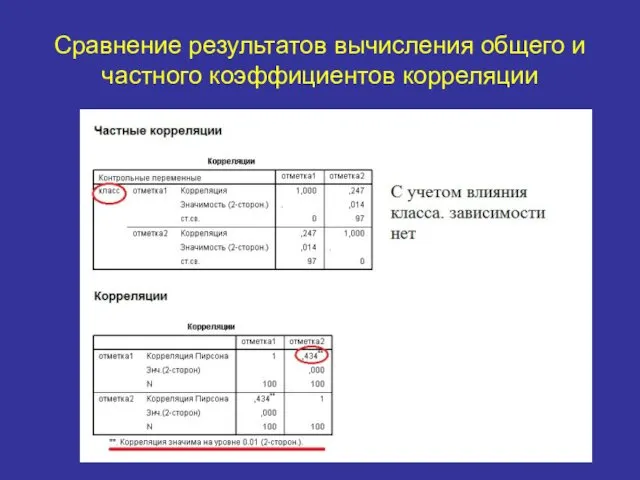
- 114. Частные корреляции Если удалось установить тесную зависимость между двумя исследуемыми величинами, отсюда ещё непосредственно не следует
- 115. Исключить влияние третьей переменной позволяет частный коэффициент корреляции. Частным коэффициентом корреляции между случайными величинами x и
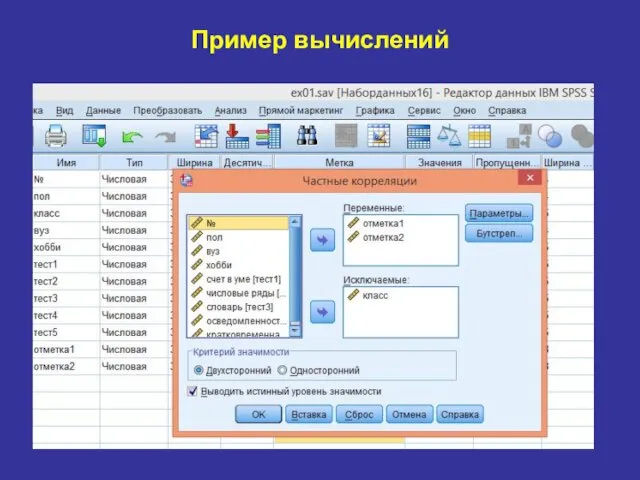
- 116. Пример вычислений
- 117. Сравнение результатов вычисления общего и частного коэффициентов корреляции
- 120. Скачать презентацию









































































 Решение текстовых задач. 9-11 классы
Решение текстовых задач. 9-11 классы Общий алгоритм действий при выполнении заданий с типовыми формулировками
Общий алгоритм действий при выполнении заданий с типовыми формулировками Золотое сечение и гармония форм природы и искусства. 8 класс
Золотое сечение и гармония форм природы и искусства. 8 класс Модуль числа. Противоположные числа
Модуль числа. Противоположные числа Простейшие преобразования графиков функций
Простейшие преобразования графиков функций Линейная алгебра и аналитическая геометрия. Дифференциальное исчисление
Линейная алгебра и аналитическая геометрия. Дифференциальное исчисление Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей Строки в таблице истинности
Строки в таблице истинности Презентация на тему Создание проблемной ситуации на уроке математики
Презентация на тему Создание проблемной ситуации на уроке математики  Тренажёр к уроку геометрии в 7 классе. УМК «Геометрия 7-9». Атанасян Л.С
Тренажёр к уроку геометрии в 7 классе. УМК «Геометрия 7-9». Атанасян Л.С Решение задач. Касательная к окружности
Решение задач. Касательная к окружности Решение задач. Повторение. 6 класс
Решение задач. Повторение. 6 класс Прямоугольник
Прямоугольник Сложение и вычитание десятичных дробей. Применение свойств сложения и вычитания
Сложение и вычитание десятичных дробей. Применение свойств сложения и вычитания Непрерывность функции одной переменной
Непрерывность функции одной переменной Indexní analýza
Indexní analýza Единицы длины
Единицы длины Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Старинные меры длины наших предков
Старинные меры длины наших предков Аттестационная работа. Исследовательская работа Определение центра тяжести плоских фигур
Аттестационная работа. Исследовательская работа Определение центра тяжести плоских фигур Подготовка к ЕГЭ по математике. Решение задач В10
Подготовка к ЕГЭ по математике. Решение задач В10 Математика и живопись
Математика и живопись Правильный многоугольник
Правильный многоугольник Презентация на тему число 8
Презентация на тему число 8 Таблица умножения на пальцах
Таблица умножения на пальцах Вводный урок математики в 1 классе
Вводный урок математики в 1 классе 02.09
02.09 Порядок выполнения действий в математике
Порядок выполнения действий в математике