Математическое описание волнового движения

Август 13, 2022

Главная
Математика
Математическое описание волнового движения

Содержание

2. Уравнения Максвелла Уравнения Максвелла в локальной и интегральной форме ВСПОМНИМ, чем завершался курс лекций 3-го семестра:
3. Уравнения Максвелла Свойства уравнений Максвелла 1. Уравнения выполняются во всех инерциальных системах отсчёта. (являются релятивистски инвариантными).
4. Ур-ния Максвелла и скорость света В изотропной среде без зарядов и токов Н = B/μ0μ ;
5. Уравнения Максвелла Уравнения Максвелла в изотропной среде без зарядов и токов div Е = 0 дB/дt
6. Решения 1-мерных уравнений Максвелла 1-мерные ур-ния Максвелла в изотропной среде без зарядов и токов д2E/дt2 =
7. Решение ур-ний Максвелла в изотропной среде без зарядов и токов д2E/дt2 = с2д2E/дх2 ; д2B/дt2 =
8. Решение одномерных ур-ний Максвелла в изотропной среде без зарядов и токов – бегущая волна E =
9. Волновое движение. Общие свойства Волны бывают разные: По природе: электромагнитные (радио, свет, и др.), упругие (звук),
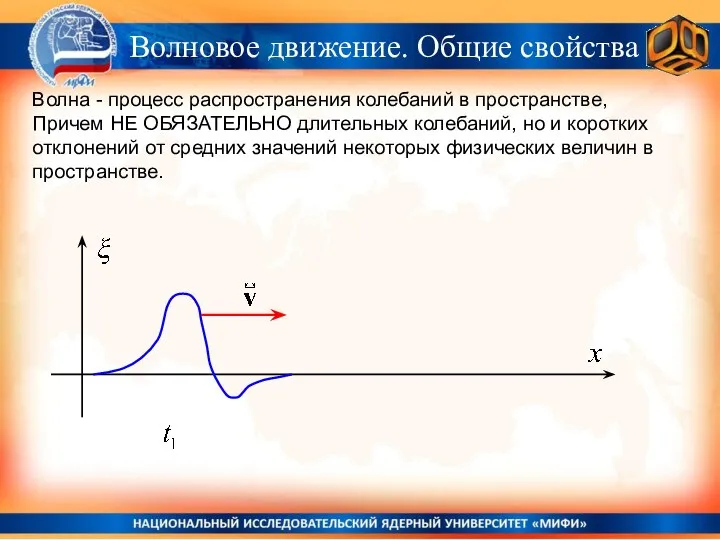
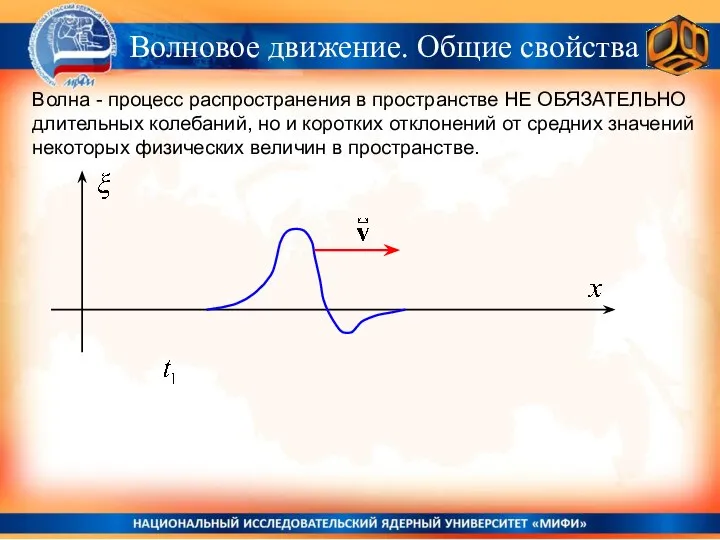
10. Волна - процесс распространения колебаний в пространстве, Причем НЕ ОБЯЗАТЕЛЬНО длительных колебаний, но и коротких отклонений
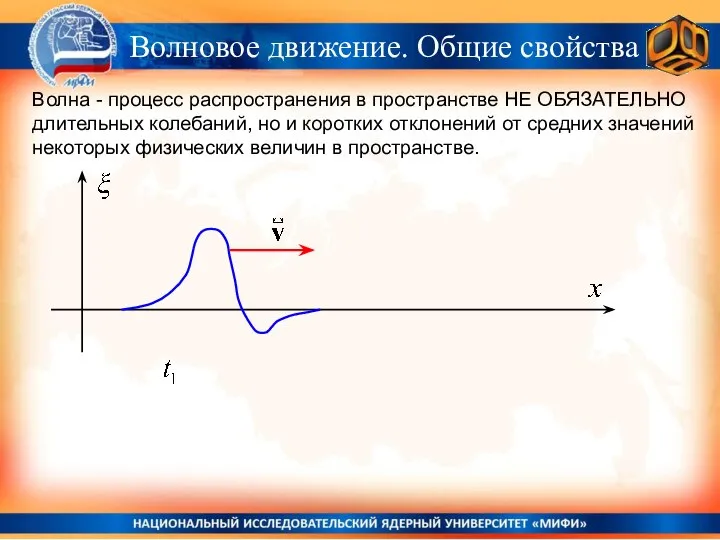
11. Волна - процесс распространения в пространстве НЕ ОБЯЗАТЕЛЬНО длительных колебаний, но и коротких отклонений от средних
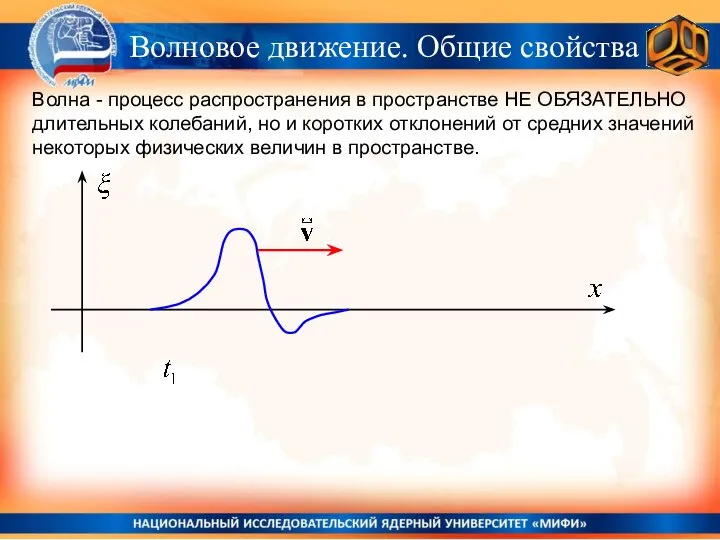
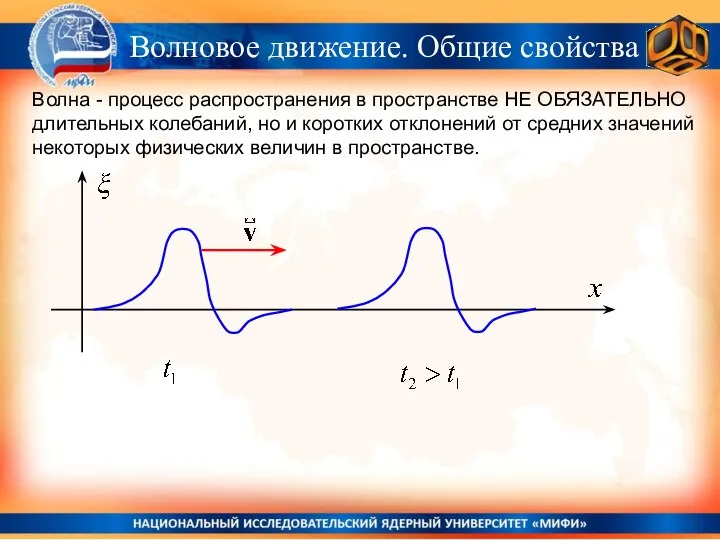
12. Волна - процесс распространения в пространстве НЕ ОБЯЗАТЕЛЬНО длительных колебаний, но и коротких отклонений от средних
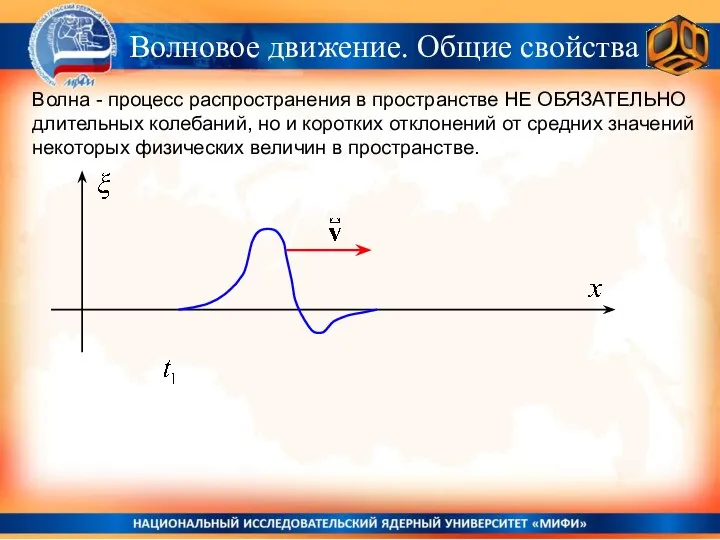
13. Волна - процесс распространения в пространстве НЕ ОБЯЗАТЕЛЬНО длительных колебаний, но и коротких отклонений от средних
14. Волна - процесс распространения в пространстве НЕ ОБЯЗАТЕЛЬНО длительных колебаний, но и коротких отклонений от средних
15. Волна - процесс распространения в пространстве НЕ ОБЯЗАТЕЛЬНО длительных колебаний, но и коротких отклонений от средних
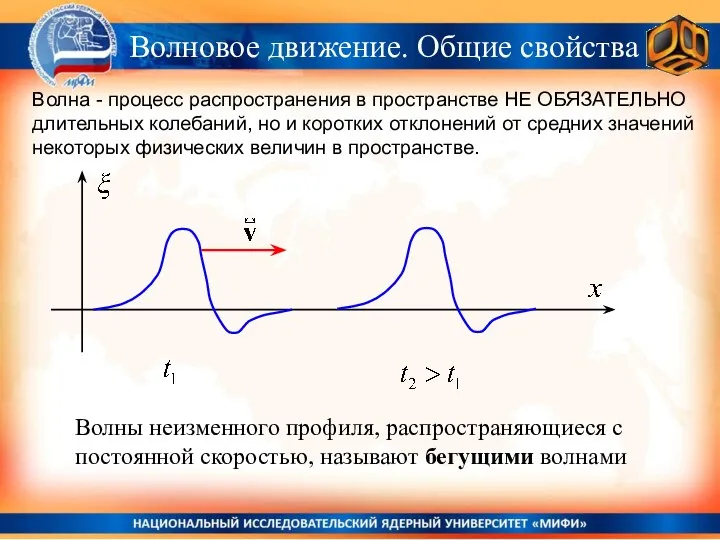
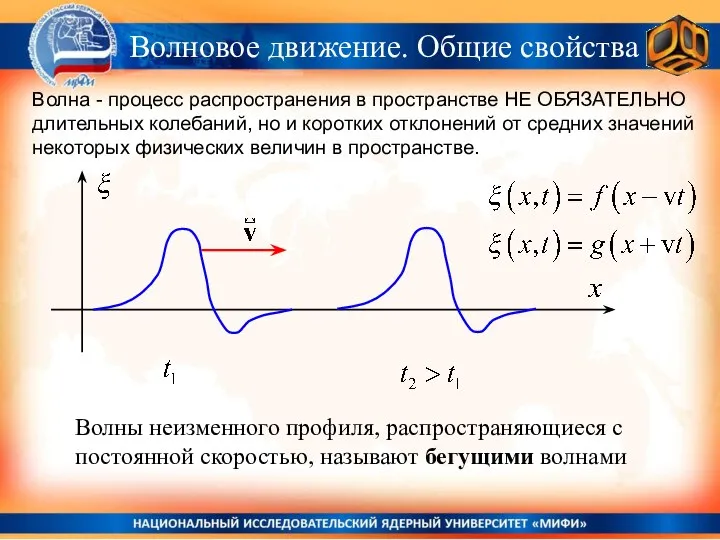
16. Волны неизменного профиля, распространяющиеся с постоянной скоростью, называют бегущими волнами Волна - процесс распространения в пространстве
17. Волны неизменного профиля, распространяющиеся с постоянной скоростью, называют бегущими волнами Волна - процесс распространения в пространстве
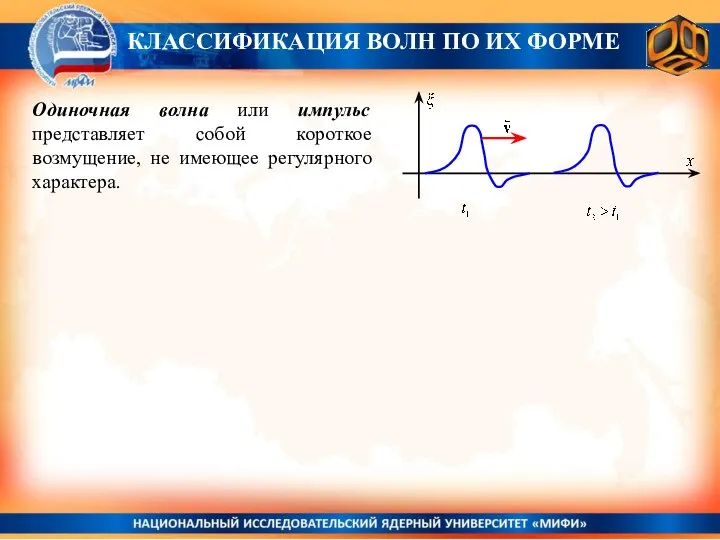
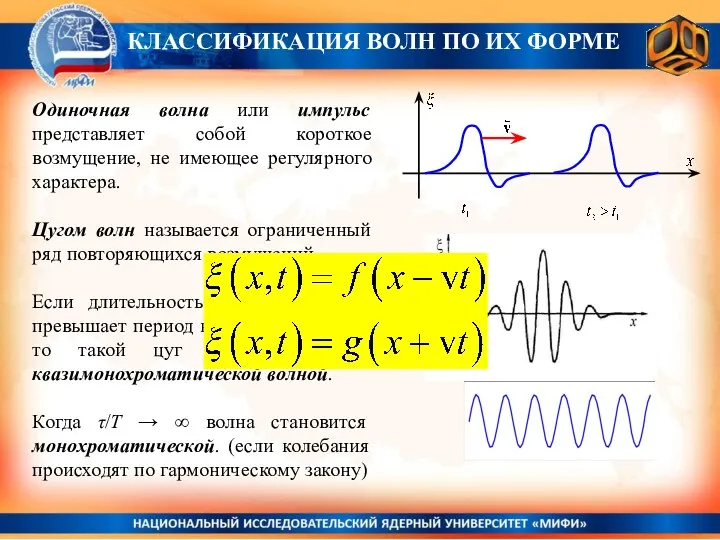
18. Одиночная волна или импульс представляет собой короткое возмущение, не имеющее регулярного характера. КЛАССИФИКАЦИЯ ВОЛН ПО ИХ
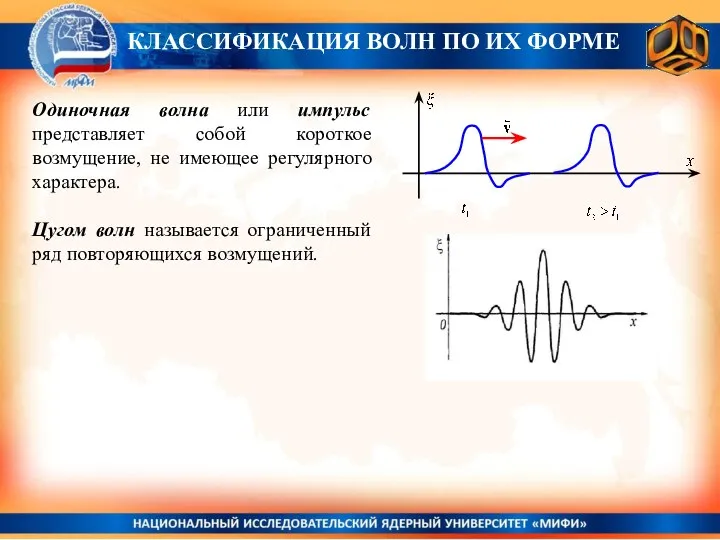
19. Одиночная волна или импульс представляет собой короткое возмущение, не имеющее регулярного характера. Цугом волн называется ограниченный
20. Одиночная волна или импульс представляет собой короткое возмущение, не имеющее регулярного характера. Цугом волн называется ограниченный
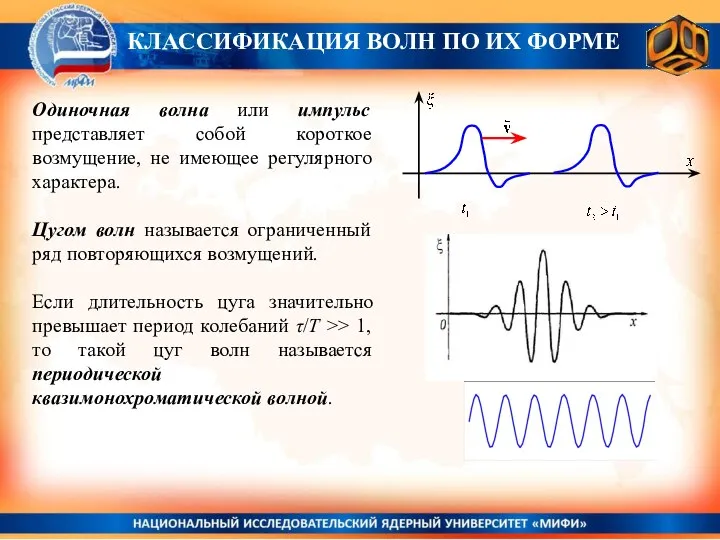
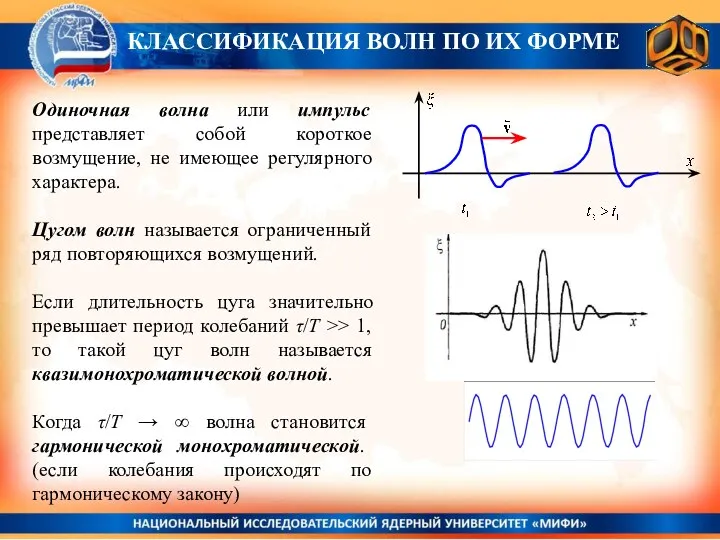
21. Одиночная волна или импульс представляет собой короткое возмущение, не имеющее регулярного характера. Цугом волн называется ограниченный
22. Одиночная волна или импульс представляет собой короткое возмущение, не имеющее регулярного характера. Цугом волн называется ограниченный
23. Волновые уравнения д2ξ /дt2 = v2д2ξ /дх2 дξ /дt = - vдξ /дх => ξ =
24. Гармоническая волна Фазовая скорость волны д2ξ /дt2 = v2д2ξ /дх2
25. Гармоническая волна = Re[a exp(i(ωt – kx+a))]
26. Одномерная волна = плоская Формально ωx/v = kx = knr = kr, k = kn =
27. Плоские гармонические волны – волновой вектор Волновая поверхность (плоскость) – геометрическое место точек, колеблющихся в одной
28. Трехмерное волновое уравнение Волновой вектор в любой точке перпендикулярен волновой поверхности. Форма волновой поверхности зависит от
29. Сферические волны Если r >> λ и d, то источник можно считать точечным, а волну на
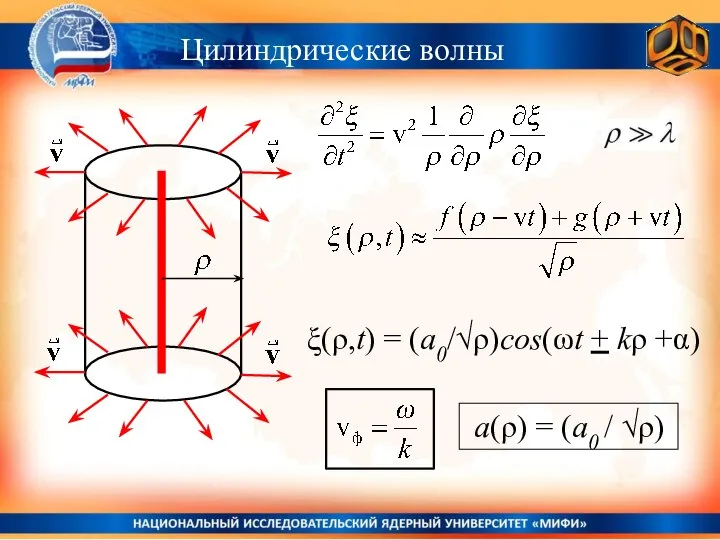
30. Цилиндрические волны ξ(ρ,t) = (a0/√ρ)cos(ωt + kρ +α) a(ρ) = (a0 / √ρ)
31. Курс общей физики НИЯУ МИФИ Следующая лекция 16 февраля
32. Примеры решения задач
33. Примеры решения задач
34. Примеры решения задач
35. Курс общей физики НИЯУ МИФИ Следующая лекция 16 февраля
36. Стоячие волны Наложение двух распространяющихся во встречных направлениях бегущих плоских волн может образовать стоячую волну:
37. Стоячие волны
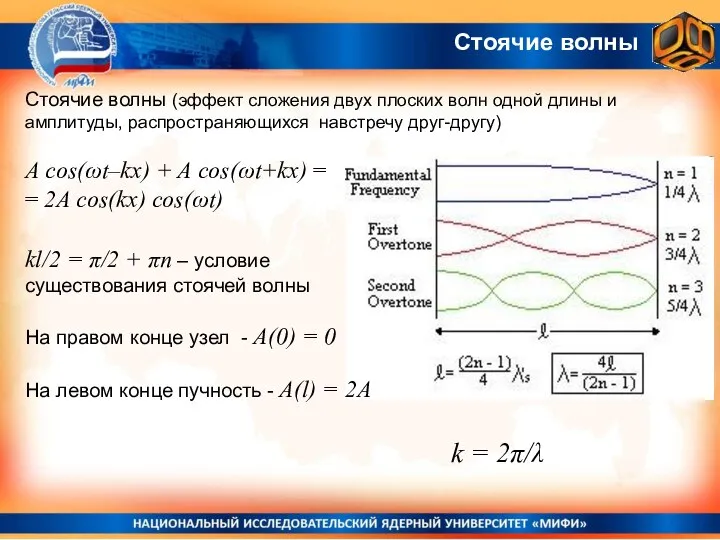
38. Стоячие волны Стоячие волны (эффект сложения двух плоских волн одной длины и амплитуды, распространяющихся навстречу друг-другу)
39. Стоячие волны Фотография стоячей волны в струне
40. Стоячие волны Стоячая волна в колоколе
41. Стоячие волны Собственные колебания Земли При очень сильном землетрясении отмечены собственные колебания Земли. От удара сдвинувшихся
42. Стоячие волны Из-за значительной ветровой нагрузки 20 мая 2010 года автомобильный мост через реку Волгу вошёл
43. Спасибо за внимание! Следующая лекция 16 февраля Общая физика, 4-ый семестр
44. Образование устойчивой структуры солитона за счёт механизма компенсации: Нелинейные волны
45. Солитон, пересекающий Гибралтарский пролив с запада на восток Нелинейные волны
46. Игрушечный кораблик в лабораторной кювете демонстрирует эффект «мертвой воды»: под его винтом образуется внутренняя волна, «высасывающая»
47. Упругие волны в газе и жидкости Снимок, сделанный спутниками НАСА у побережья Австралии, показывает разновидность гигантских
49. Скачать презентацию

Слайд 2

Уравнения Максвелла
Уравнения Максвелла в локальной и интегральной форме
ВСПОМНИМ, чем завершался курс

лекций 3-го семестра:
Дж.К. Максвелл в 1859 г. сформулировал систему уравнений, исчерпывающим образом описывающих единое электро-магнитное поле.

Слайд 3

Уравнения Максвелла
Свойства уравнений Максвелла
1. Уравнения выполняются во всех инерциальных системах отсчёта.

(являются релятивистски инвариантными).
2. Уравнения линейные, благодаря чему выполняется принцип суперпозиции для магнитных и электрических полей.
3. Уравнения не симмметричны относительно E и B => эти поля проявляют себя по разному.
4. Уравнения содержат все известные законы электродинамики: Кулона, Био-Савара-Лапласа, уравнение непрерывности и т.п.
5. Из уравнений Максвелла следует возможность существования и распространения электромагнитных волн в вакууме.

Слайд 4

Ур-ния Максвелла и скорость света
В изотропной среде без зарядов и токов

Н = B/μ0μ ; D = ε0 εE

div D = div Е = 0 rot E = -дB/дt
div B = 0 rot Н = +дD/дt = >
=> rot B/μ0μ = ε0 εдE/дt
=> rot B = μ0με0 ε дE/дt = (1/c2)дE/дt
с = (μ0με0 ε)-1/2 [м/с] – скорость света в среде μ, ε
с0 = (μ0ε0)-1/2 = 3*108м/с - скорость света в пустоте μ=ε=1
= максимально возможная скорость распространения чего бы то ни было во Вселенной
с = (μ0με0 ε)-1/2 = с0 (με)-1/2 =~ с0/ε 1/2 = с0 /n =>
Оптическая плотность среды (показатель преломления) n =~ ε1/2
Удивительные результаты, обнаружившие ранее не замеченную связь оптики и электромагнетизма

Слайд 5

Уравнения Максвелла
Уравнения Максвелла в изотропной среде без зарядов и токов
div Е

= 0 дB/дt = - rot E
div B = 0 дE/дt = +с2rot B = >
«Поиграем» с дифференциальными операторами
д2В/дt2 = - д(rot Е)/дt = - с2rot rot B =
= - с2(grad div B - ∆B) = с2∆B
д2E/дt2 = с2д(rot B)/дt = - с2rot rot E = с2∆E
Система уравнений Максвелла в изотропной среде без зарядов и токов сводится всего к ДВУМ математически одинаковым уравнениям, определяющим поведение электрической Е и магнитной В компонент поля, и имеющим волновые решения.

Слайд 6

Решения 1-мерных уравнений Максвелла
1-мерные ур-ния Максвелла в изотропной среде без зарядов

и токов

д2E/дt2 = с2∆E = с2д2E/дх2 ; д2B/дt2 = с2д2В/дх2
Решение: т.н. бегущая волна
E = Е0 f(y) , В = В0 f(y); y = x+tс
f – любая (!) математическая функция одной переменной y = x+tс.
ДОКАЖЕМ. дE/дt = (дE/дy)(дy/дt) = +c дE/дy;
д2E/дt2 = +c(д2E/дy2(дy/дt) = c2 д2E/дy2
с2∆E = с2д2E/дx2 = с2д2E/дy2 Ч.Т.Д. !
Конкретный вид функции f определяется т.н. начальными условиями задачи – то есть, видом функции распределения полей Е(х), В(х) в начальный момент времени t = 0

Слайд 7

Решение ур-ний Максвелла в изотропной среде без зарядов и токов
д2E/дt2 =

с2д2E/дх2 ; д2B/дt2 = с2д2В/дх2
Решение (в одномерном случае): т.н. бегущая волна
E = Е0 f(x+сt)) , В = В0 f(x+ct))
Конкретный вид функции f определяется начальными условиями задачи – т.е. видом функций Е(х), В(х) в момент времени t = 0
ПРИМЕР. E(x, t=0) = Е0 cos(2πx/λ)) = Е0 cos(ωx/c) =>
E(x, t) = Е0 cos(ω(x + ct)/c) = Е0 cos(2πx/λ + ωt) =>
=> E(x, t) = Е0 cos(2π(x/λ + t/T)
Если начальная конфигурация поля = гармоническая функция, такой она останется и далее, но как-бы «побежит» по оси ОХ (если аргумент (х - сt) или против оси ОХ (если (х+ct). Чтобы определить, куда бежит волна, надо знать второе начальное условие: вид производной функции дE(x, t)/ дt при t = 0

Волновые решения уравнений Максвелла

Слайд 8

Решение одномерных ур-ний Максвелла в изотропной среде без зарядов и токов

– бегущая волна

E = Е0 f(x+сt)) , В = В0 f(x+ct))
Конкретный вид функции f определяется начальными условиями задачи – т.е. видом функций Е(х), В(х) в момент времени t = 0
и видом производных этих функций при t = 0.
Это – электромагнитные волны – очень важное физическое явление, которое необходимо всесторонне изучать.
Нужность изучения математического описания волнового движения усугубляется тем, что волны бывают не только электромагнитные (радио, свет, и др.), но и упругие (звук), капилярно-гравитационные (на поверхности жидкости) и т.д., и т.п.
Волна – особая, очень распространенная форма движения материи

Волновые решения уравнений Максвелла

Слайд 9

Волновое движение. Общие свойства
Волны бывают разные:
По природе: электромагнитные (радио, свет,

и др.), упругие (звук), капиллярно-гравитационные (на поверхности жидкости) и т.д., и т.п.
По пространственным характеристикам: одномерные (плоские), сферические, цилиндрические, …
По форме: одиночные, цуговые, периодические, гармонические
… а также бывают волны бегущие и стоячие, продольные и поперечные, сходящиеся и расходящиеся, нелинейные, ударные, …. и со всеми надо постепенно разобраться….

Слайд 10