Mathematical Induction

Mathematical Induction

Let Sn, n = 1,2,3,… be statements involving positive integer

for all positive integers n. If it is assumed that the

Therefore, the principle of mathematical induction tells us that for any

in both parts of the relationship

But, what if this is a

Question 1:

Answers to Questions from Light #2:
Sequences and Limits

Question 2:

Question

Calculus++

Also known as Hysterical Calculus

Question 1b. Find the limit of the sequence

Solution. We have

Using the

Using now the equivalence

we obtain

Therefore,

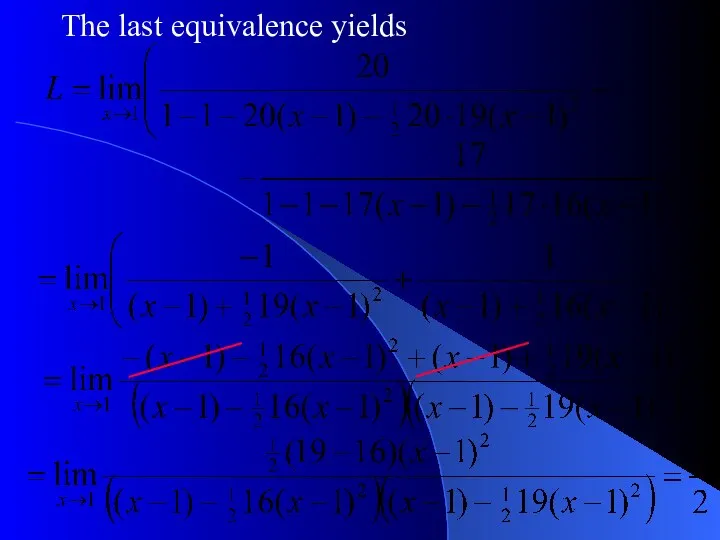
Question 2b. Find the following limit

Solution. Actually, the equivalence

gives an incorrect

The last equivalence yields

Question 3. Find the following limit

Solution. We have to find precise

A similar (but even more difficult) calculation yields

Therefore

and

Picture of the Week

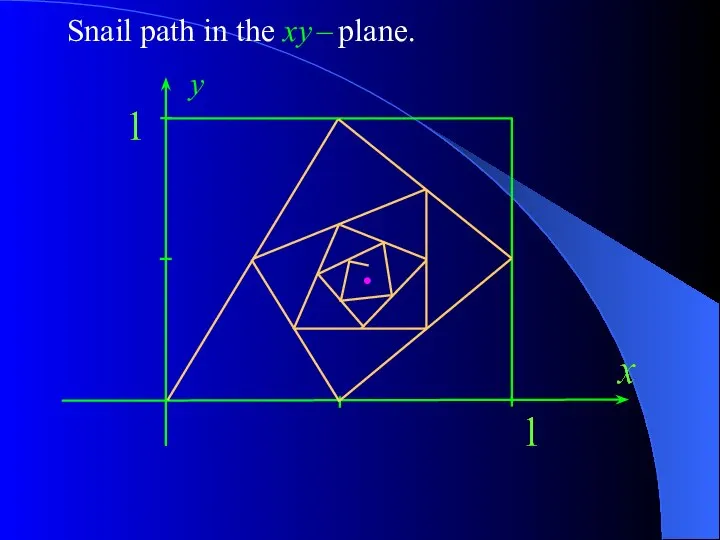
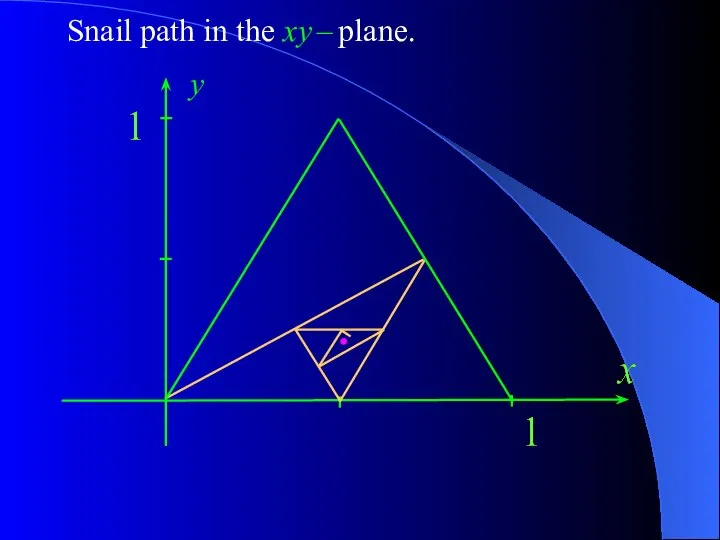
Question 8. The initial location of a snail is the point

a) Show that xn+3 + xn+2 + xn+1 + ½ xn

Snail path in the xy – plane.

y

Solution. Write down the characteristic equation for the formula

Unfortunately, this

Therefore

Thus

If the sequence xn converges to , then

Passing to

Snail path in the xy – plane.

y