Содержание
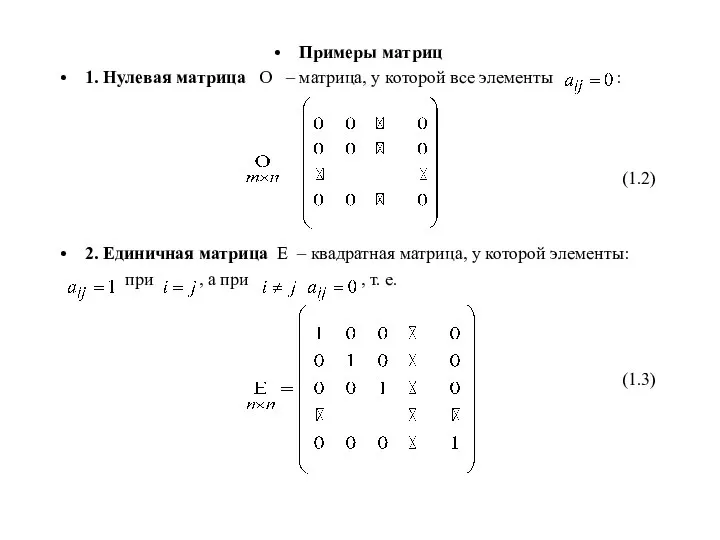
- 2. Примеры матриц 1. Нулевая матрица О – матрица, у которой все элементы : (1.2) 2. Единичная
- 3. 3. Диагональная матрица – квадратная матрица, у которой элементы: при , а при : (1.4) 4.
- 4. Замечание. «Главной диагональю» произвольной матрицы называют группу элементов , , … , (при ), либо группу
- 5. либо при m (1.7) Определение 1.2 (равенство матриц). Матрица А называется равной матрице В (А =
- 6. Определение 1.3 (сумма двух матриц). Пусть даны две матрицы и , тогда суммой А + В
- 7. Свойства операций над матрицами 1) – коммутативность, 2) , 3) , , 4) Произведение матриц зависит
- 8. Замечание. – умножение невозможно. Кроме того: Определение 1.6. Дана квадратная матрица . Обратной матрицей к матрице
- 10. Скачать презентацию






 Умножение десятичных дробей на натуральные числа. 5 класс
Умножение десятичных дробей на натуральные числа. 5 класс Прикладная математика. Угол
Прикладная математика. Угол Сложение и вычитание двузначных чисел без перехода через десяток
Сложение и вычитание двузначных чисел без перехода через десяток  Итоговый тест по математике. 5 класс
Итоговый тест по математике. 5 класс «РАЦИОН ПИТАНИЯ УЧАЩИХСЯ 6-Х КЛАССОВ В ПРОЦЕНТАХ И ДИАГРАММАХ» МОБУ СОШ №1 им. И.Д. Бувальцева МО Кореновский район Деркачева Екат
«РАЦИОН ПИТАНИЯ УЧАЩИХСЯ 6-Х КЛАССОВ В ПРОЦЕНТАХ И ДИАГРАММАХ» МОБУ СОШ №1 им. И.Д. Бувальцева МО Кореновский район Деркачева Екат Построения циркулем и линейкой (7 класс)
Построения циркулем и линейкой (7 класс) Алгебра и начала математического анализа
Алгебра и начала математического анализа Назначение формулы
Назначение формулы Путешествие по графику
Путешествие по графику Четырехугольники. Проверочная работа по чертежам
Четырехугольники. Проверочная работа по чертежам Теория пределов. Лекция 1
Теория пределов. Лекция 1 Путешествие по стране "Дроби". 5 класс
Путешествие по стране "Дроби". 5 класс Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Теорема Піфагора
Теорема Піфагора Академия развития интеллекта. Ментальная арифметика
Академия развития интеллекта. Ментальная арифметика Регрессионные модели с переменной структурой (фиктивные переменные)
Регрессионные модели с переменной структурой (фиктивные переменные) Деревья. Компьютерная дискретная математика
Деревья. Компьютерная дискретная математика Теорема косинусов
Теорема косинусов Задачи на построение
Задачи на построение Площадь параллелограмма
Площадь параллелограмма Ряды динамики
Ряды динамики Координатная плоскость
Координатная плоскость Относительные величины: типы, определение, методика вычисления, применение
Относительные величины: типы, определение, методика вычисления, применение Игра «Брейн-ринг». Внеклассное занятие
Игра «Брейн-ринг». Внеклассное занятие Презентация по математике "Пифагор" - скачать
Презентация по математике "Пифагор" - скачать  Неопределенный интеграл. Методы интегрирования. Лекция 2
Неопределенный интеграл. Методы интегрирования. Лекция 2 Решение задач «на проценты», смеси и сплавы
Решение задач «на проценты», смеси и сплавы Повторяем таблицу умножения вместе с Машей
Повторяем таблицу умножения вместе с Машей