Содержание
- 2. Введем обозначения
- 3. Тогда исходную систему запишем относительно векторной функции F векторного аргумента Следовательно, исходную задачу можно рассматривать как
- 4. Однако, переход от к вносит в задачу нахождения нулей свою специфику. Метод Ньютона решения систем нелинейных
- 5. или в компактной форме: Для задачи о неподвижной точке нелинейного отображения запишем
- 6. формальное равенство: где определяет метод простых итераций и Пусть известно - е приближение одного из изолированных
- 7. Тогда точный корень уравнения можно представить: где поправка (погрешность корня). Имеем Предполагая, что непрерывно дифференцируема в
- 8. членами Под производной следует понимать матрицу Якоби системы функций относительно переменных т.е.
- 9. Тогда Если то Следовательно, метод Ньютона для решения исходной системы состоит в построении итерационной последовательности: k=0,1,2,
- 10. Пример. Найти методом Ньютона решение системы уравнений исходя из начального приближения
- 11. Полагая имеем
- 12. Подставляя данные, получаем Составим матрицу Якоби:
- 13. При этом Т.к. то найдем обратную ей матрицу
- 14. Получим первое приближение:
- 15. а Аналогично находим дальнейшие приближения В результате получим ( )
- 16. Решение нелинейных систем методами спуска Общий недостаток всех рассмотренных ранее методов решения систем нелинейных уравнений состоит
- 17. Пусть задана система Образуем новую функцию Т.к. эта функция не отрицательна, то всегда найдется точка такая,
- 19. Т.е., если удается получить точку минимизирующую функцию и если при этом окажется, что то точка истинное
- 20. Последовательность точек приближений к точке минимума функции получают по формуле где вектор, определяющий направление минимизации, а
- 21. Исходя из геометрического смысла задачи, итерационный метод называется методом спуска. При выборе направления спуска определяющим является
- 22. Направление наибольшего возрастания функции в данной точке показывает её градиент в этой точке. Поэтому антиградиент функции
- 23. Тогда суть градиентного метода Достоинство градиентного метода решения нелинейных систем – глобальная сходимость. Главный недостаток –
- 24. Пример. Найти максимум функции Методом скорейшего спуска при ограничениях: Функция является выпуклой, поэтому её локальный максимум
- 25. Пусть исходная точка Подставляя координаты в выражение градиента, получим Используя формулу получим Используя скалярное произведение векторов
- 26. найдём Отсюда а=0,7449 – величина длины шага. Тогда координаты следующей точки и градиента:
- 27. Выполняя в цикле представленные расчёты, процесс итерации заканчиваем при достижении заданной точности отклонения В нашем примере
- 28. Пример. Найти направление наискорейшего возрастания функции в точке и вычислить значение производной в этом направлении. Решение.
- 30. Скачать презентацию



























 Методическая разработка раздела образовательной программы по математике «Квадратные уравнения». 8 класс
Методическая разработка раздела образовательной программы по математике «Квадратные уравнения». 8 класс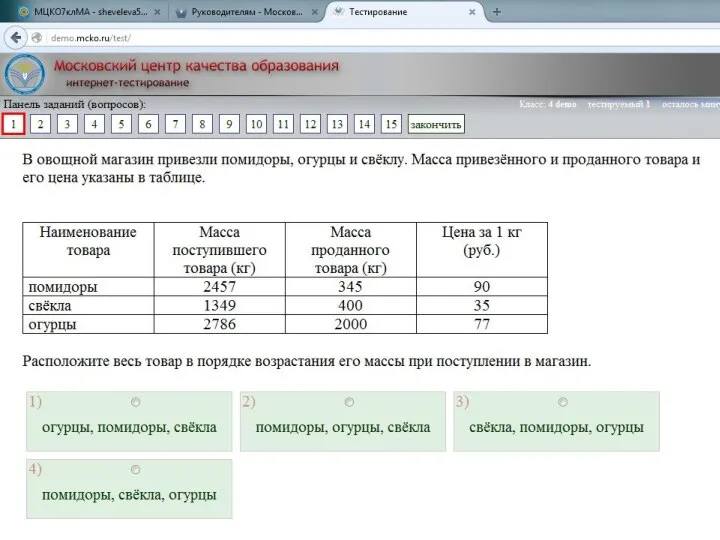 Московский центр качества образования. Интернет-тестирование
Московский центр качества образования. Интернет-тестирование Задачі з геометрії за готовими малюнками
Задачі з геометрії за готовими малюнками Машинное обучение и анализ данных. Линейные модели. Логистическая регрессия
Машинное обучение и анализ данных. Линейные модели. Логистическая регрессия Функция у=arccos x
Функция у=arccos x Великие о математике
Великие о математике Додавання і віднімання в межех 20. Веселий потяг
Додавання і віднімання в межех 20. Веселий потяг Тест по теме: "Конус"
Тест по теме: "Конус" Предмет, метод, задачи статистики и принципы организации государственной статистики в РФ
Предмет, метод, задачи статистики и принципы организации государственной статистики в РФ Матричний підхід до лінійної багатофакторної моделі
Матричний підхід до лінійної багатофакторної моделі Презентация по математике "Отрезок. Длина отрезка. Треугольник. Задания по теме" - скачать
Презентация по математике "Отрезок. Длина отрезка. Треугольник. Задания по теме" - скачать  Решение квадратных неравенств
Решение квадратных неравенств Деление числа на произведение
Деление числа на произведение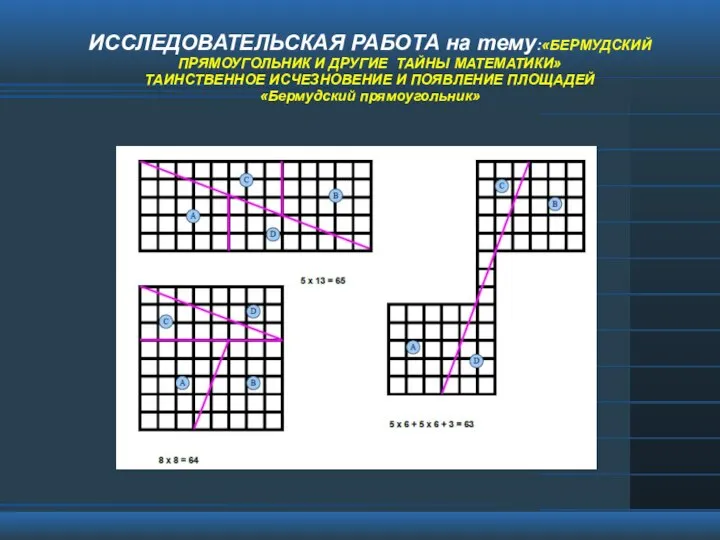 «Бермудский прямоугольник и другие тайны математики», таинственное исчезновение и появление площадей
«Бермудский прямоугольник и другие тайны математики», таинственное исчезновение и появление площадей Детерминационный, факторный и кластерный анализ
Детерминационный, факторный и кластерный анализ Виды многогранников
Виды многогранников Простейшие задачи в координатах
Простейшие задачи в координатах Жозеф Луи Лагранж (1736-1813)
Жозеф Луи Лагранж (1736-1813) Введение в компьютерный и интеллектуальный анализ данных (ВКИАД). Типы статистических данных и способы их первичной обработки
Введение в компьютерный и интеллектуальный анализ данных (ВКИАД). Типы статистических данных и способы их первичной обработки Деление с остатком. 5 класс
Деление с остатком. 5 класс Аттестационная работа. Решение задач повышенной сложности
Аттестационная работа. Решение задач повышенной сложности Признаки делимости на 2, 5, 10 (5 класс) - Презентация
Признаки делимости на 2, 5, 10 (5 класс) - Презентация Логические задачи
Логические задачи Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными Золотое сечение в искусстве. Золотое сечение в живописи и фотографии
Золотое сечение в искусстве. Золотое сечение в живописи и фотографии Основное свойство дроби
Основное свойство дроби 7 класс МБСЛШ им. Ю.А. Гагарина Учитель: И.А. Глазырина
7 класс МБСЛШ им. Ю.А. Гагарина Учитель: И.А. Глазырина  Приемы устного счета Учитель математики Бадюк Ольга Ярославна, МКОУ «Москаленский лицей»
Приемы устного счета Учитель математики Бадюк Ольга Ярославна, МКОУ «Москаленский лицей»