Содержание
- 2. Минимизация упрощение формы записи схема реализуется с наименьшим числом элементов
- 3. Минимальная нормальная форма Нормальная форма логической функции, содержащая наименьшее число элементов Минимальная ДНФ = МДНФ Минимальная
- 4. Методы минимизации Непосредственных преобразований Квайна и Мак-Класки Карно-Вейча
- 5. МЕТОД НЕПОСРЕДСТВЕННЫХ ПРЕОБРАЗОВАНИЙ Минимизация логических функций
- 6. Метод непосредственных преобразований Применение законов алгебры логики Результат − тупиковая форма логической функции
- 7. Тупиковая форма Логическое выражение, к слагаемым которого больше не могут быть применены операции склеивания Для одной
- 8. Функции a и b называются равносильными, если при одинаковых входных данных они принимают одинаковые значения a
- 9. ЗАКОНЫ ЛОГИКИ
- 10. 1. Идемпотентность a & a ≡ a a ∨ a ≡ a
- 11. 2. Коммутативность a & b ≡ b & a a ∨ b ≡ b ∨ a
- 12. 3. Ассоциативность a & (b & с) ≡ (a & b) & с a ∨ (b
- 13. 4. Дистрибутивность a & (b∨с) ≡ (a & b) ∨ (a & с) a ∨ (b
- 14. 5. Закон двойного отрицания ¬(¬a) ≡ a
- 15. 6. Законы поглощения a & (a ∨ b) ≡ a a ∨ (a & b) ≡
- 16. 7. Законы де Моргана ¬(a ∨ b) ≡ ¬a & ¬ b ¬(a & b) ≡
- 17. 8. Закон исключённого третьего ¬a ∨ a ≡ 1
- 18. 9. Закон противоречия ¬a & a ≡ 0
- 19. 10. Свойства тавтологии и противоречия 1 & a ≡ a 1 ∨ a ≡ 1 0
- 20. 11. Законы склеивания (a & b) ∨ (a & ¬b) ≡ a (a ∨ b) &
- 21. 12. Законы поглощения a & (a ∨ b) ≡ a a ∨ (a & b) ≡
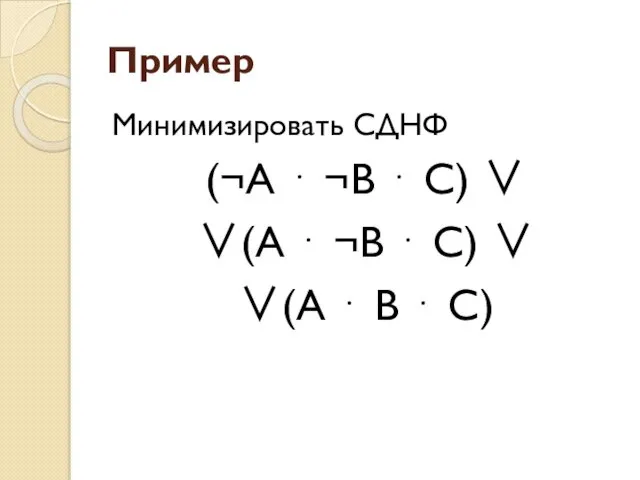
- 22. Пример Минимизировать СДНФ (¬А ⋅ ¬В ⋅ С) ∨ ∨(А ⋅ ¬В ⋅ С) ∨ ∨(А
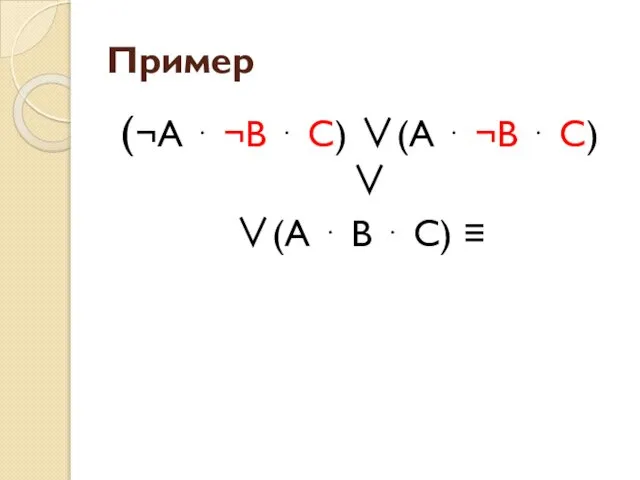
- 23. Пример (¬А ⋅ ¬В ⋅ С) ∨(А ⋅ ¬В ⋅ С) ∨ ∨(А ⋅ В ⋅
- 24. Пример (¬А ⋅ ¬В ⋅ С) ∨(А ⋅ ¬В ⋅ С) ∨ ∨(А ⋅ В ⋅
- 25. Пример (¬А ⋅ ¬В ⋅ С) ∨(А ⋅ ¬В ⋅ С) ∨ ∨(А ⋅ В ⋅
- 26. Пример (¬А ⋅ ¬В ⋅ С) ∨(А ⋅ ¬В ⋅ С) ∨ ∨(А ⋅ В ⋅
- 27. Пример (¬А ⋅ ¬В ⋅ С) ∨(А ⋅ ¬В ⋅ С) ∨ ∨(А ⋅ В ⋅
- 30. Проблема Определить, какие элементарные конъюнкции / дизъюнкции надо склеивать
- 31. КАРТЫ ВЕЙЧА-КАРНО Минимизация логических функций
- 32. Эдвард Вестбрук Вейч Американский физик 1952 «Метод диаграмм для минимизации логических функций» 1924 — 2013
- 33. Морис Карно род. 1924 Американский физик 1953 Усовершенствовал метод Вейча
- 34. Карта Карно Графическое представление таблицы истинности логических функций Таблица, содержащая по 2n прямоугольных ячеек, где n
- 35. Код Грея система счисления, в которой два соседних значения различаются только в одном разряде
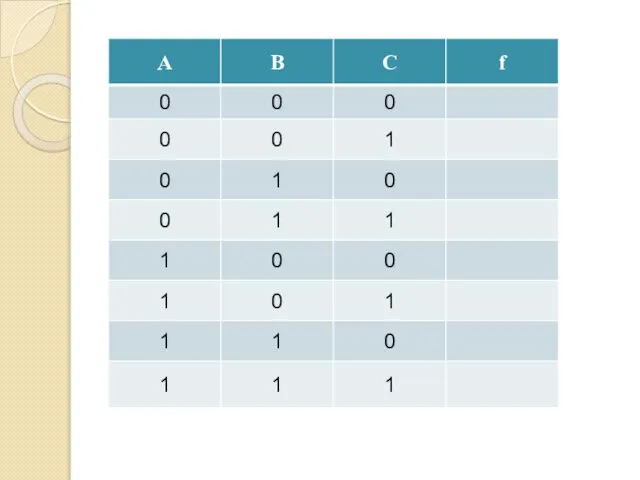
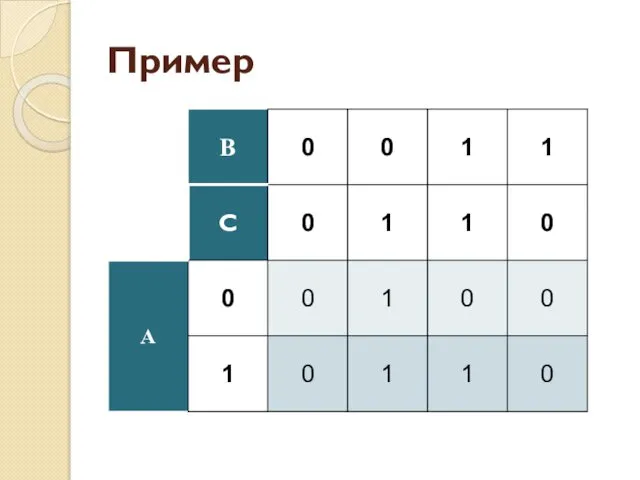
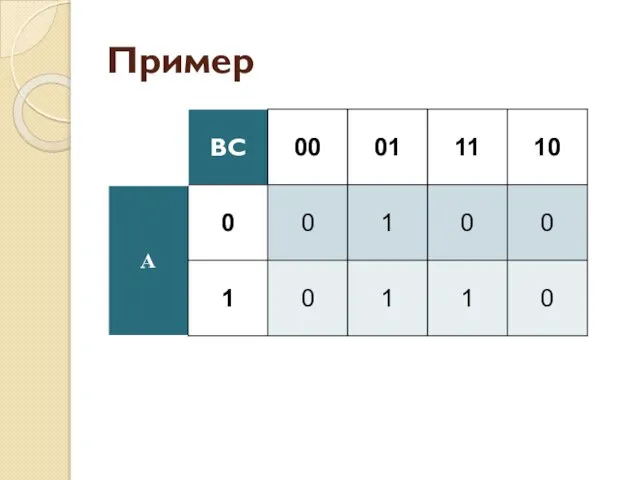
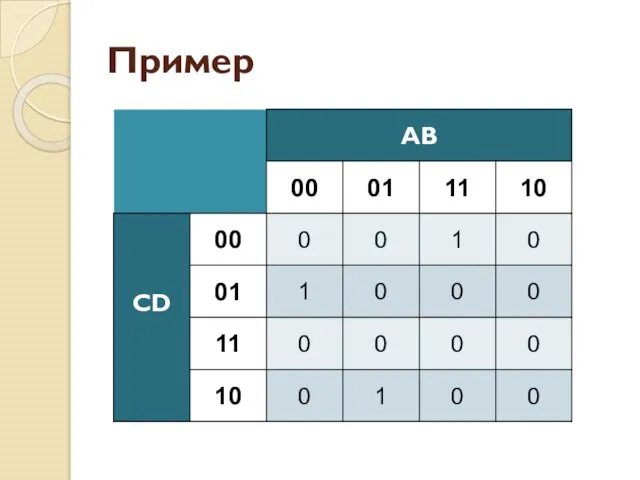
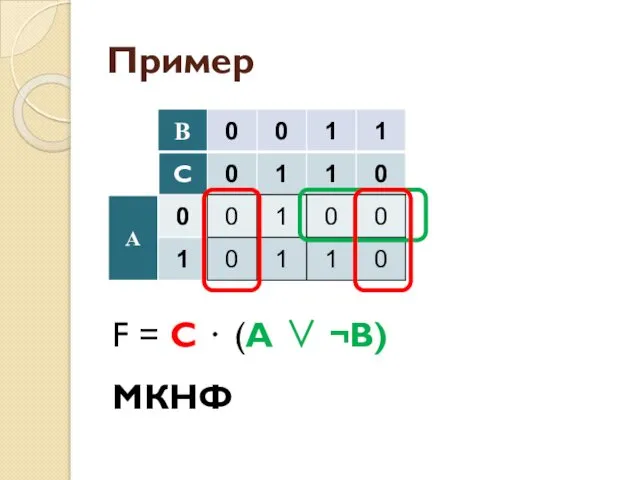
- 36. Пример
- 37. Пример
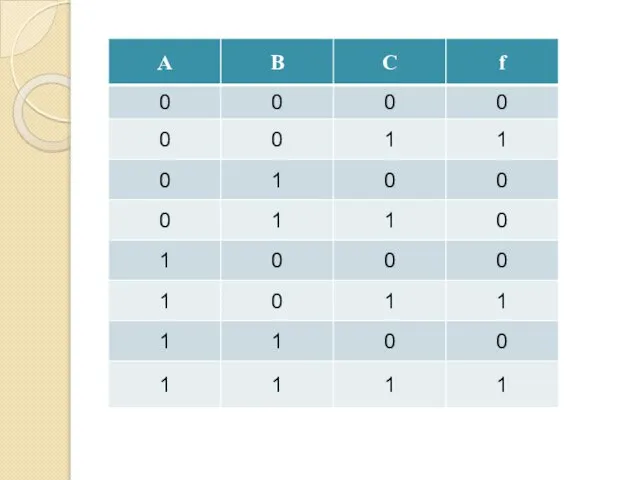
- 38. Пример
- 39. Пример
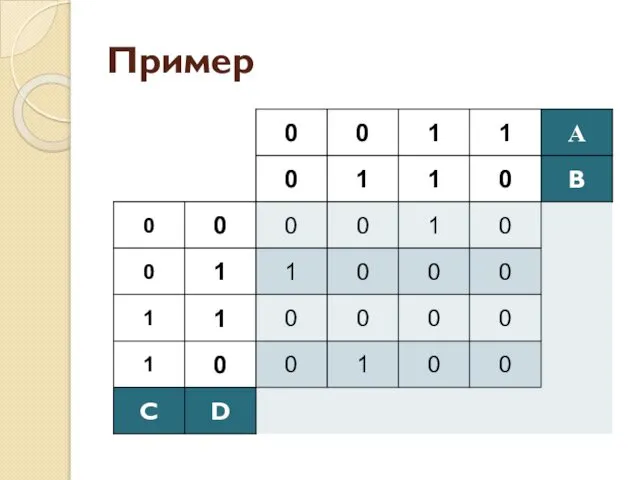
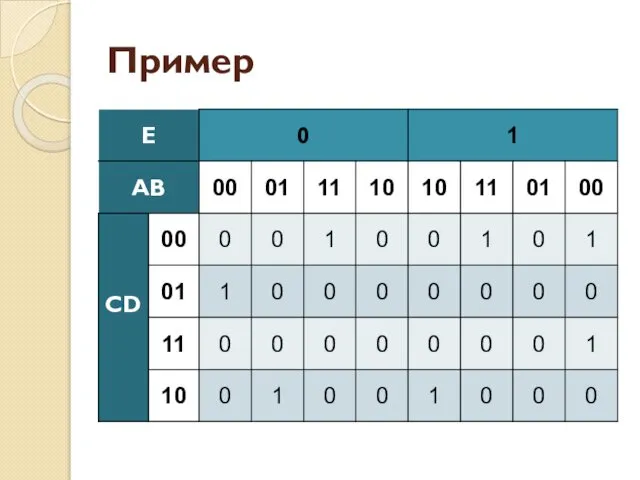
- 41. Пример
- 42. Пример
- 43. Пример
- 44. Правила ДНФ КНФ 1. Объединяем смежные клетки с единицами (нулями) в максимально возможные области, содержащие 2n
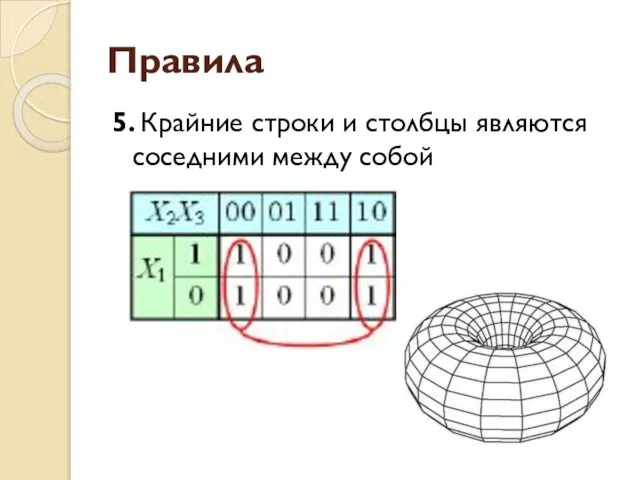
- 45. Правила 5. Крайние строки и столбцы являются соседними между собой
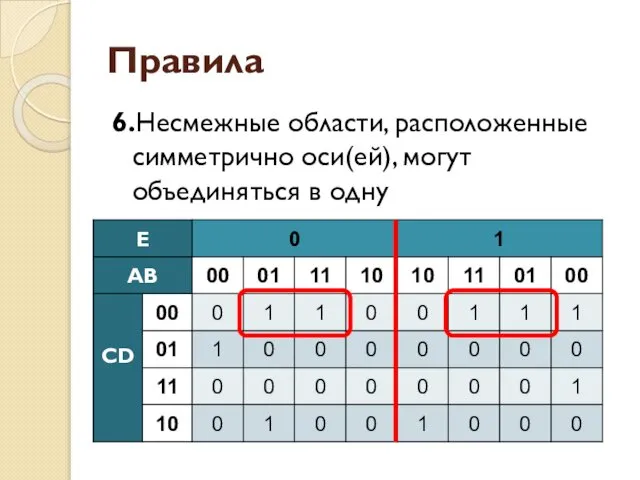
- 46. Правила 6.Несмежные области, расположенные симметрично оси(ей), могут объединяться в одну
- 47. Правила 7. Для каждой области записываем конъюнкцию (дизъюнкцию) переменных, не изменяющих своё значение Если неизменная переменная
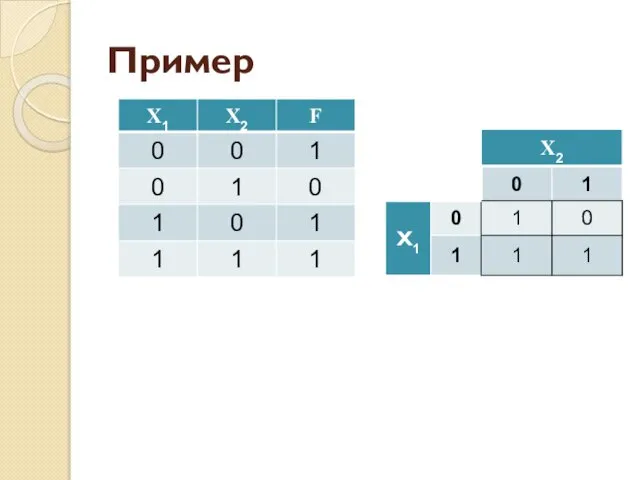
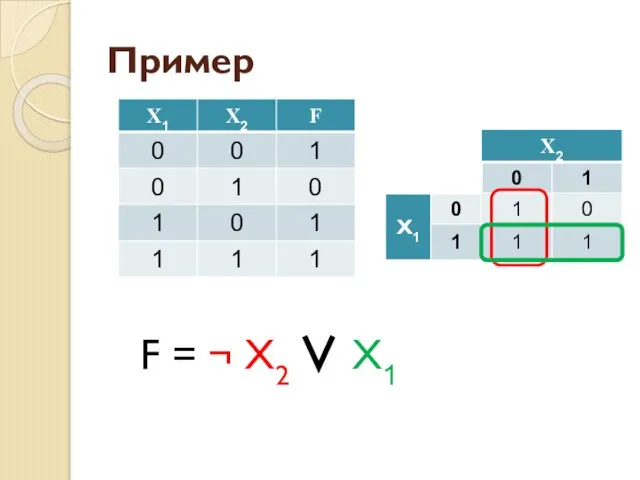
- 48. Пример F = ¬ X2 ∨ X1
- 49. Пример ‒ МДНФ F = X1 ⋅¬ X2 ∨ ¬X1⋅ X2
- 50. Пример ‒ МКНФ F = (X1 ∨ X2) ⋅ (¬X1∨ ¬ X2)
- 51. Пример
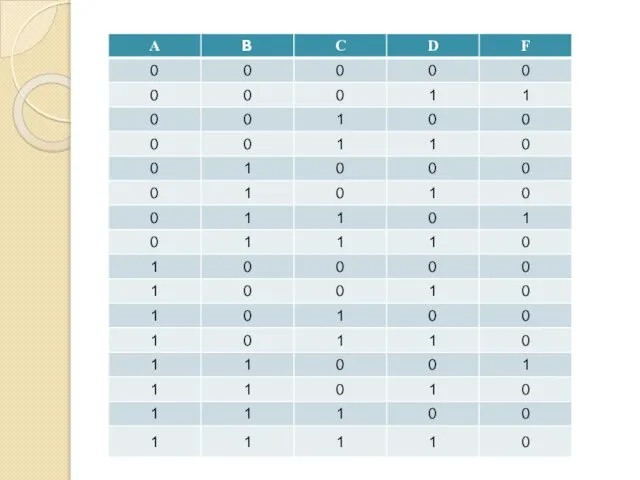
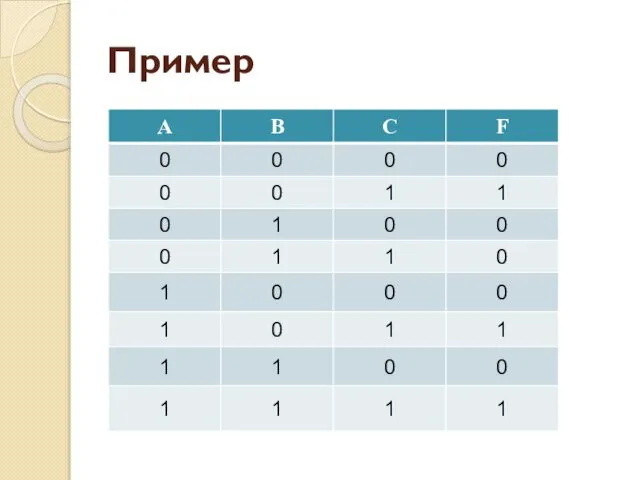
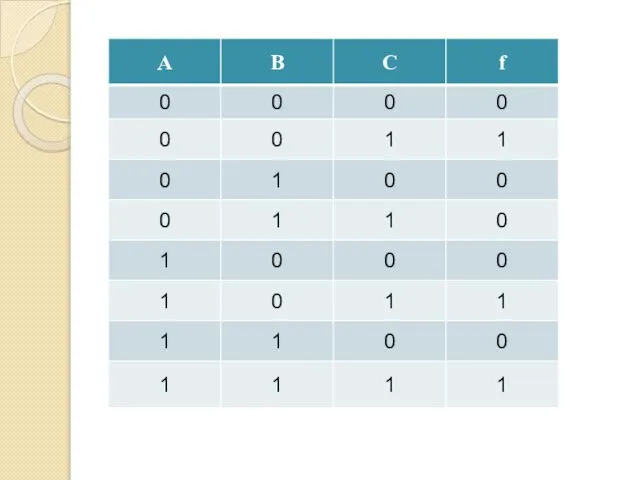
- 52. Формула (¬А ⋅ ¬В ⋅ С) ∨ ∨(А ⋅ ¬В ⋅ С) ∨ ∨(А ⋅ В
- 53. (А ∨ В ∨ С) ⋅ ⋅ (А ∨ ¬В ∨ С) ⋅ ⋅ (А ∨¬
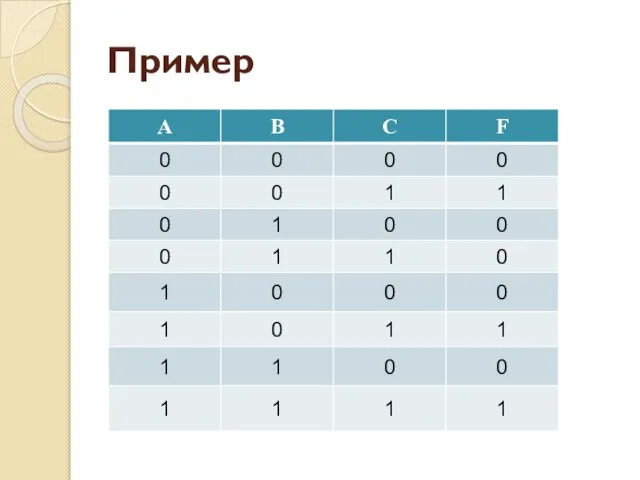
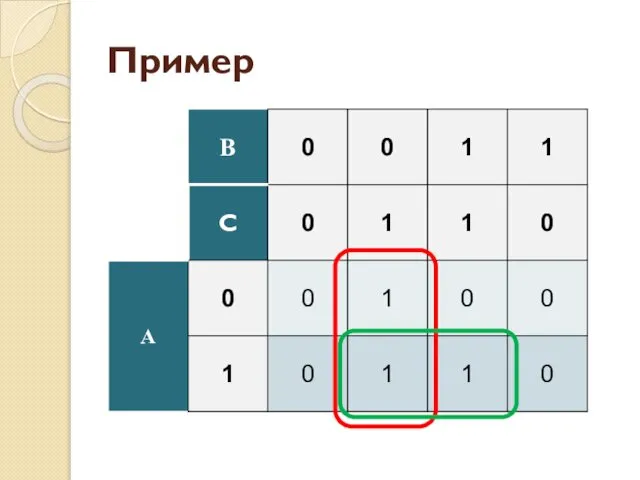
- 54. Пример
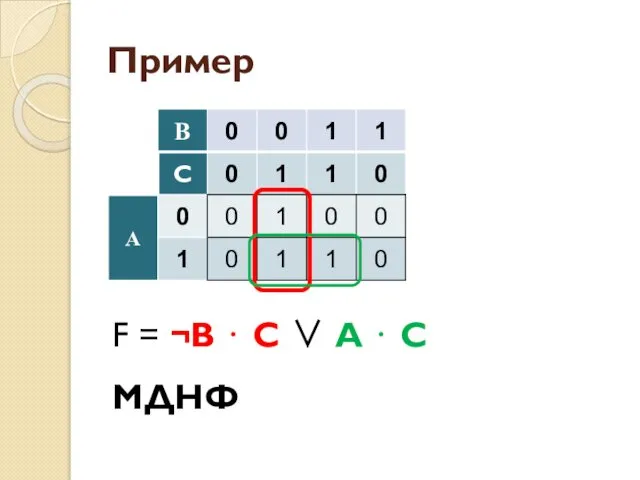
- 55. Пример F = ¬В ⋅ С ∨ A ⋅ C МДНФ
- 56. Пример F = С ⋅ (A ∨ ¬В) МКНФ
- 58. Недостатки Применим для функций до 7 переменных Выбор областей ‒ визуально Нет алгоритма, обеспечивающего оптимальное решение
- 59. МЕТОД КВАЙНА И МАК-КЛАСКИ Минимизация логических функций
- 60. Виллард ван Орман Куайн Американский философ, логик и математик 1993 премия Рольфа Шока в области логики
- 61. Эдвард Дж. Мак-Класки Почётный профессор Стэнфордского университета. Пионер в области электротехники Первый алгоритм проектирования комбинационных схем
- 63. Скачать презентацию







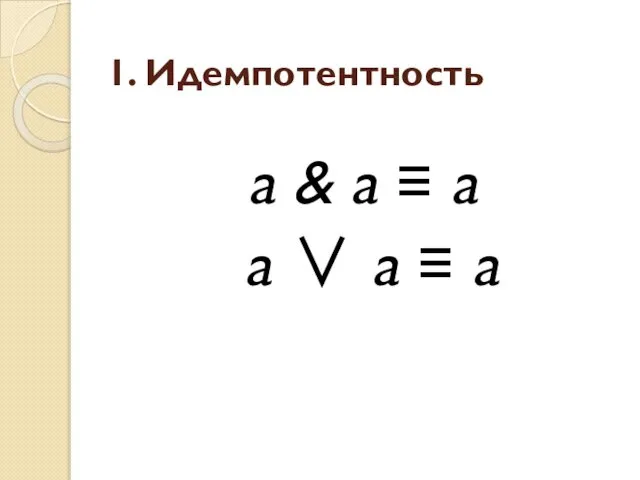































 Сучасні методи наближення функцій багатьох змінних (інтерлінація)
Сучасні методи наближення функцій багатьох змінних (інтерлінація) Формулы приведения
Формулы приведения Подобие треугольников. Применение подобия к решению задач
Подобие треугольников. Применение подобия к решению задач Математика повсюду
Математика повсюду Презентация по математике "Измерения" - скачать бесплатно
Презентация по математике "Измерения" - скачать бесплатно Дискретная математика. Периоды развития математики
Дискретная математика. Периоды развития математики Квадратные уравнения. Решение уравнений
Квадратные уравнения. Решение уравнений Презентация по математике "Число 3. цифра 3" - скачать
Презентация по математике "Число 3. цифра 3" - скачать  ВГУЭС Кафедра математики и моделирования
ВГУЭС Кафедра математики и моделирования  Исследование функции. Геометрический смысл производной
Исследование функции. Геометрический смысл производной Основные понятия теории вероятности. Случайные события
Основные понятия теории вероятности. Случайные события Состав чисел
Состав чисел Второй признак равенства треугольников
Второй признак равенства треугольников Площади плоских геометрических фигур
Площади плоских геометрических фигур Устный счет - гимнастика для ума. Способы быстрого счёта
Устный счет - гимнастика для ума. Способы быстрого счёта Показательные уравнения
Показательные уравнения Сумма углов треугольника
Сумма углов треугольника Система подготовки учащихся к ЕГЭ по математике. Леухина Эра Анатольевна 29.02.2012.
Система подготовки учащихся к ЕГЭ по математике. Леухина Эра Анатольевна 29.02.2012.  Лабораторно-практическая работа в парах
Лабораторно-практическая работа в парах Счастливый случай. Игра
Счастливый случай. Игра Расчет надежности систем с восстановлением
Расчет надежности систем с восстановлением Вычисление площадей плоских фигур
Вычисление площадей плоских фигур Решение квадратных уравнений по формуле. 8 класс
Решение квадратных уравнений по формуле. 8 класс Презентация по математике "Рабочая программа учителя математики" - скачать
Презентация по математике "Рабочая программа учителя математики" - скачать  Круг и окружность
Круг и окружность Проценты. Жить или курить?
Проценты. Жить или курить? Santas sleigh. Game
Santas sleigh. Game Решение показательного уравнения
Решение показательного уравнения