Содержание
- 2. Периоды развития математики В истории цивилизации можно выделить три крупных периода: сельскохозяйственный, или аграрный — до
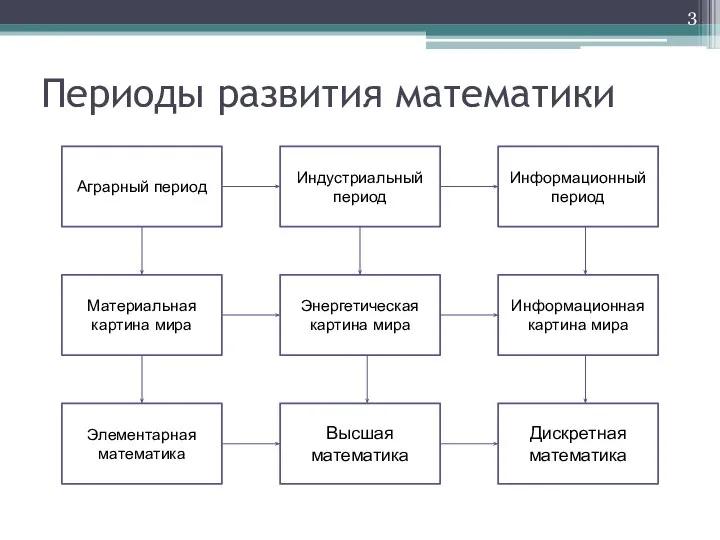
- 3. Периоды развития математики
- 4. Дискретной математикой называют совокупность математических дисциплин, изучающих свойства абстрактных дискретных объектов. Фундаментом дискретной математики являются: Теория
- 5. Стимулы развития дискретной математики: растущий поток информации и проблемы ее передачи, обработки и хранения привели к
- 6. Обозначения Кванторы: Квантор общности: ∀ - «любой», «всякий», «каждый»; Квантор существования: ∃ - «существует», «найдется», «можно
- 7. Теория множеств Дискретная математика
- 8. Основные понятия «Под многообразием, или множеством, я понимаю вообще всякое многое, которое можно мыслить как единое,
- 9. Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в
- 10. Примеры множеств: Множество решений уравнения; Множество студентов в группе; Множество предметов мебели в кабинете; Множество натуральных
- 11. Универсальное множество Множество U, содержащее все возможные элементы, обладающие некоторым признаком, называется универсальным (универсумом). . Пример:
- 12. Множества обозначают большими буквами латинского алфавита. Элементы множества – строчными буквами. «элемент, а принадлежит множеству М»
- 13. Множества удобно изображать с помощью кругов Эйлера (диаграмм Венна). Леонард Эйлер (1707 – 1783г.) Диаграммы Эйлера-Венна
- 14. Определение равенства множеств 1. Два множества называются равными (А=В) в том и только в том случае,
- 15. Множество A называют подмножеством множества B (обозначается A ⊆ B ), если всякий элемент множества A
- 16. Определение равенства множеств 2. Множества A и B равны ( A=B ) тогда и только тогда,
- 17. Булеаном множества М называется множество β(М), элементами которого являются все возможные подмножества множества М. Булеан множества
- 18. Множество, состоящее из конечного числа элементов называется конечным множеством. Бесконечное множество- непустое множество, не являющееся конечным.
- 19. Способы задания множеств Множества могут быть заданы списком; порождающей процедурой; описанием характеристических свойств элементов; графическим представлением.
- 20. Задание множеств списком предполагает перечисление элементов. Например: множество А состоит из букв a,b,c,d. Обозначается: А={a,b,c,d} множество
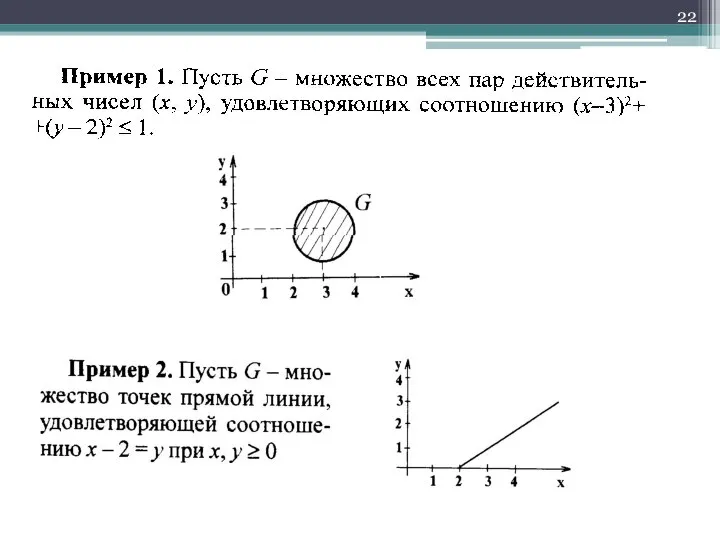
- 21. Задание множеств порождающей процедурой, которая описывает способ получения элементов множества из уже полученных элементов либо других
- 23. Задание множеств порождающей процедурой, которая описывает способ получения элементов множества из уже полученных элементов либо других
- 24. Задайте списком множество: 1) букв в слове «алгебра»; 2) четных однозначных натуральных чисел; 3) нечетных однозначных
- 25. По какому характеристическому свойству записаны такие множества: {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}; {январь, февраль,
- 26. Операции над множествами Объединением множеств A и B (A∪B) называется множество, состоящее из всех тех элементов,
- 27. Пересечением множеств A и В называется множество (А∩В), состоящее из тех и только тех элементов, которые
- 28. Операции над множествами Разностью множеств A и B (A\B) называется множество всех элементов множества A, которые
- 29. Разностью множеств B и A (B\A) называется множество всех элементов множества B, которые не содержатся в
- 30. Операции над множествами Симметрической разностью множеств А и В (А Δ В или А ⊕ В)
- 31. Операции над множествами Дополнением (до универсального множества) множества А ( А ) называется множество всех элементов,
- 33. Кортежем длины n (n-кой) называется упорядоченная последовательность из n элементов. Элемент, занимающий первое место, называется первой
- 34. Известно, что M = {1;2;5}, N = {1;4;5;7;9}, K = {4;7;9}. Найдите: 1) пересечение M и
- 35. т Операции над множествами
- 36. Найти булеан множества М={a,b,c}. β(М)={∅, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}}. Найти булеан множества М={1,3,5,7}
- 37. Домашнее задание Дано: U={1, 2, 3, 4, 5, 6, 7}, A={1, 2, 3, 4, 5}, В={2,
- 38. Свойства операций над множествами Пусть U — универсальное множество; A, B,C— его подмножества. Тогда имеют место
- 39. Свойства операций над множествами Идемпотентность объединения и пересечения законы де Моргана тождества поглощения А ∪ (А
- 40. Доказательства
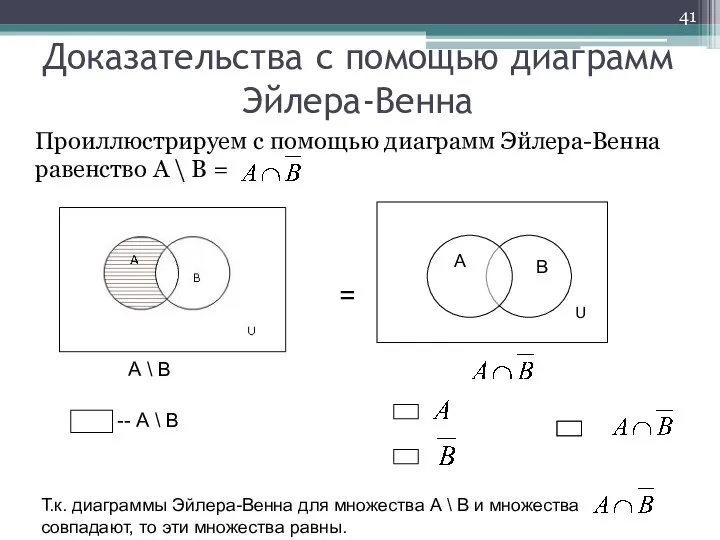
- 41. Проиллюстрируем с помощью диаграмм Эйлера-Венна равенство А \ В = Доказательства с помощью диаграмм Эйлера-Венна А
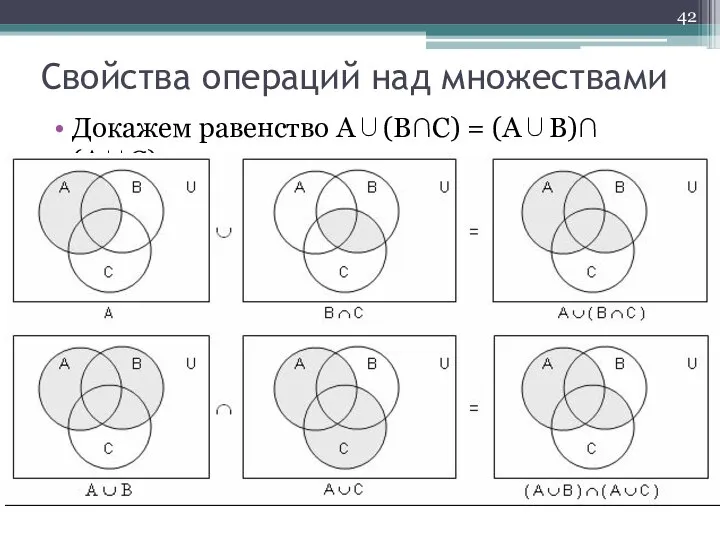
- 42. Докажем равенство А∪(В∩С) = (А∪В)∩(А∪С). Свойства операций над множествами
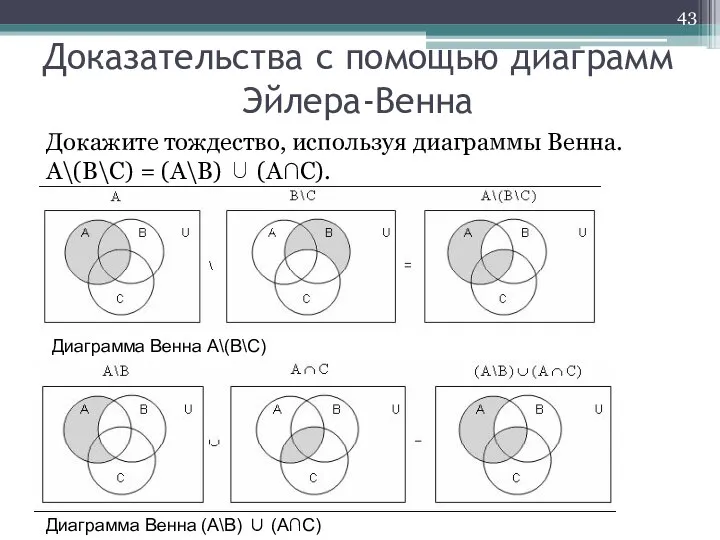
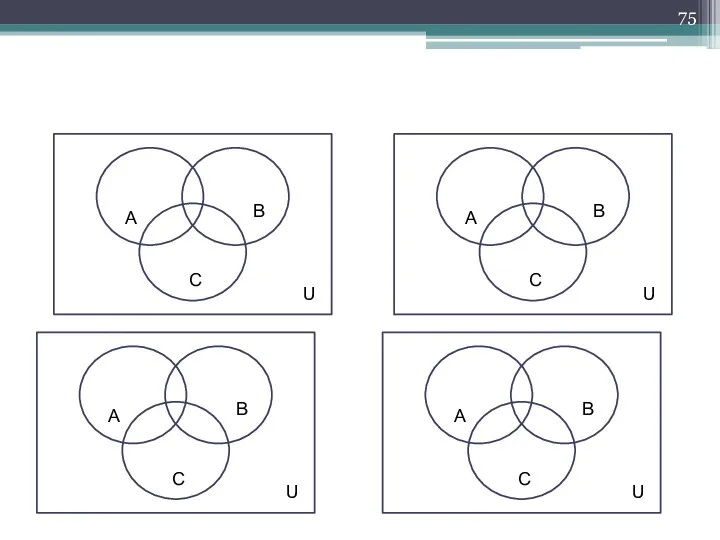
- 43. Доказательства с помощью диаграмм Эйлера-Венна Докажите тождество, используя диаграммы Венна. А\(В\С) = (А\В) ∪ (А∩С). Диаграмма
- 44. Доказать, что: A\(BC)=(A\B)(A\C), A\(BC)=(A\B)(A\C), A\(A\B)=AB, A\B=A\(AB), A(B\C)=(AB)\(AC)=(AB)\C, (A\B)\C=(A\C)\(B\C), AB=A(B\A), (AB)(A )=A, (AB)(A )=A, ( B)A=AB, (AB)\C=(A\C)(B\C),
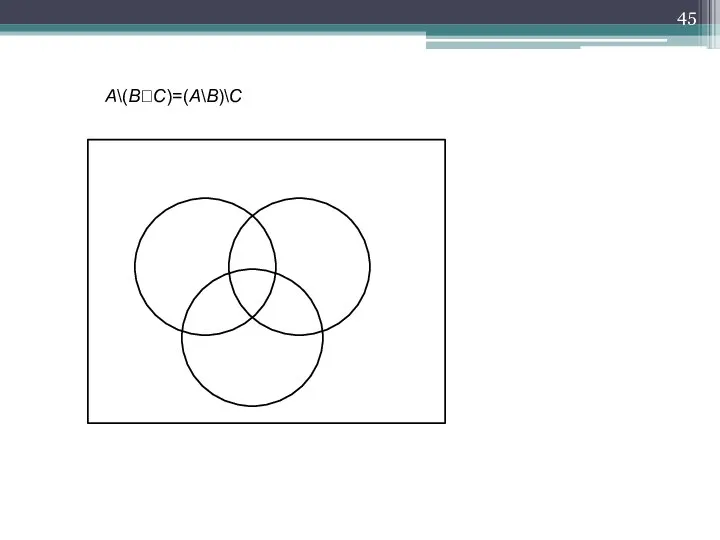
- 45. A\(BC)=(A\B)\C
- 46. Доказательства (аналитически) Справедливость законов алгебры множеств доказывается на основе определения равенства: Х = Y, если 1)
- 47. Используя отношения принадлежности, доказать тождество (A Δ B) \ C = (A \ C) Δ (B
- 48. 2) Если y ∈ Y ⇒ y ∈ (A \ C) Δ (B \ C) ⇒
- 49. Отсюда или = или . Доказательства Следовательно тождество верно.
- 50. 1) Если Доказательства Докажем закон дистрибутивности: Доказательство. и и или или
- 51. Докажем включение в обратную сторону: Доказательства Если или или и и ⊆ Так как и ⊆
- 52. Операции над множествами Тест
- 53. Вставьте слово или фразу Пересечением множеств A и В называется множество, состоящее из тех и только
- 54. Вставьте слово или фразу Разностью множеств B и A называется множество всех элементов множества B, которые_______________________
- 55. Объединением множеств A и B называется множество, состоящее из всех тех элементов, которые_________________ принадлежат множествам А
- 56. Симметрической разностью множеств А и В называется множество, содержащее те и только те элементы, которые____ принадлежат
- 57. 5.Установите соответствие 5 2 3 4 1 6
- 58. 6.Выбрать верное утверждение
- 59. Выбрать верный вариант ответа: 7.
- 60. 8. Выбрать верный вариант ответа
- 61. 9. Выбрать верный вариант ответа
- 62. 10. Выбрать верный вариант ответа
- 63. Выбрать все верные утверждения: 11.
- 64. Выбрать все верные утверждения: 12. Найти элементы множества F:
- 65. Выбрать верный вариант ответа: 13.
- 66. 14.
- 67. 15.Установите соответствие x ∈ A ∩ B ⇒ x ∉ A ∩ B ⇒ x ∈
- 68. |A∪B ∪C|= 16. Выбрать верный вариант ответа:
- 70. Решение задач Операции над множествами
- 71. Даны множества K={а,б,д}, L={б,в,д}, M={а,в,г}, U={а,б,в,г,д}. Найти множества: (K∩M) \L L∪(K M) M×L ∇
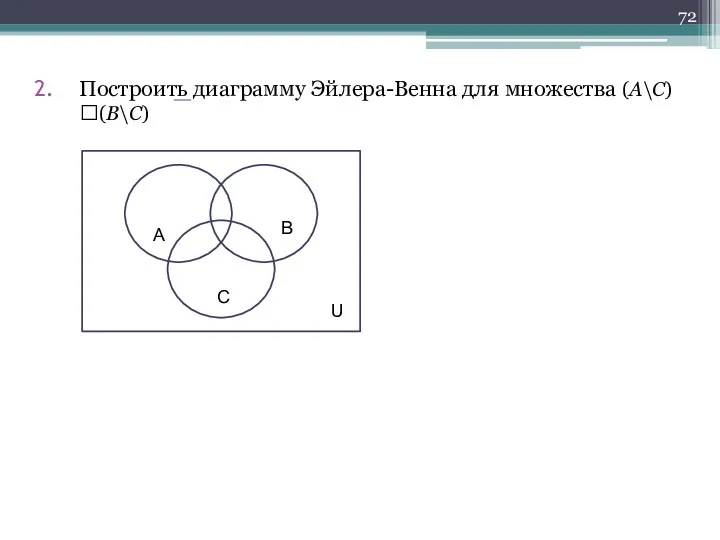
- 72. Построить диаграмму Эйлера-Венна для множества (A\C)(B\C)
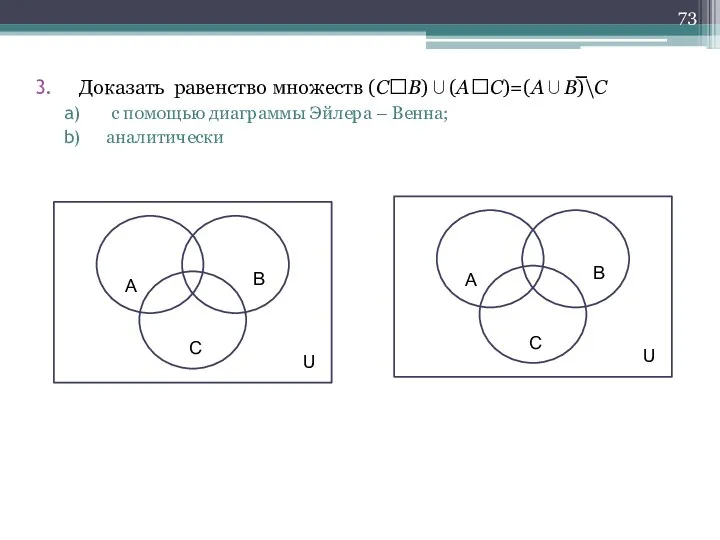
- 73. Доказать равенство множеств (СB)∪(AC)=(A∪B)\C с помощью диаграммы Эйлера – Венна; аналитически
- 74. Доказать равенство множеств (СB)∪(AC)=(A∪B)\C б) аналитически
- 76. Нахождение мощности объединения множеств Мощность объединения двух множеств равна сумме мощностей этих множеств баз мощности их
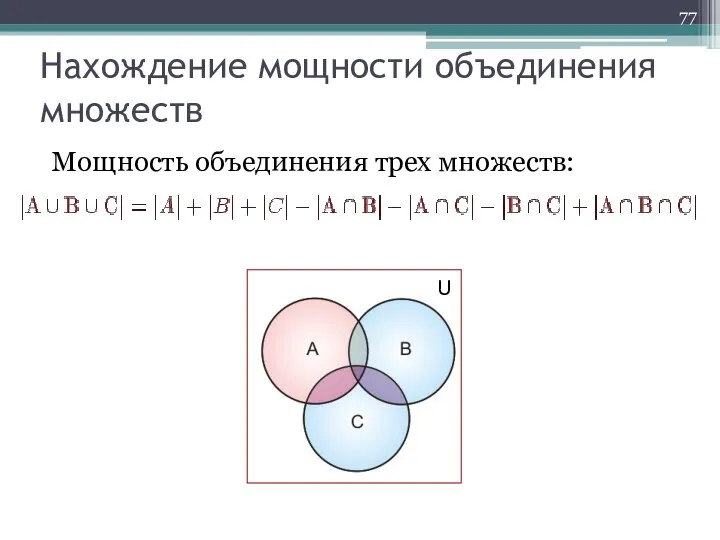
- 77. Мощность объединения трех множеств: Нахождение мощности объединения множеств
- 78. Пример. На потоке из 100 студентов 28 человек изучают английский язык, 30 человек - немецкий язык,
- 79. H- мн-во студентов, изучающих нем. язык , ⏐H⏐=30; Ф- мн-во студентов, изучающих фр. язык, ⏐Ф⏐=42. Соответственно
- 80. Задача. На вступительном экзамене по математике были предложены три задачи: по алгебре, планиметрии и стереометрии. Из
- 81. Задача. В студенческой группе 25 человек. Во время летних каникул 9 из них выезжали в турпоездки
- 82. Задача. Из 220 школьников 163 умеют играть в хоккей, 175 – в футбол, 24 не умеют
- 83. Задача. По итогам экзаменов из 37 студентов отличную оценку по математике имели 15 студентов, по физике
- 84. Задача. Староста курса представил следующий отчет о физкультурной работе: Всего – 45 студентов. Футбольная секция –
- 85. В течение 30 дней сентября было 12 дождливых, 8 ветреных, 4 холодных, 5 дождливых и ветреных,
- 86. Подготовка к контрольной работе
- 87. 3. Докажите, что Даны множества K={а,б,д}, L={б,в,д}, M={а,в,г}, U={а,б,в,г,д}. Найти множества: (K∪ M) \L L ∩
- 89. Скачать презентацию












































































 Решение задач. Закрепление. 2 класс
Решение задач. Закрепление. 2 класс Признаки делимости на 4, на 25
Признаки делимости на 4, на 25 Урок 15 Действия с многочленами
Урок 15 Действия с многочленами  Лабороторная работа 2 ВТ 20-1
Лабороторная работа 2 ВТ 20-1 Сечения многогранника (задачи)
Сечения многогранника (задачи) Линейная функция и её график. Урок-соревнование «Звездный час»
Линейная функция и её график. Урок-соревнование «Звездный час» Состав числа. Палочки Кюизенера
Состав числа. Палочки Кюизенера Закон на построение
Закон на построение Теория вероятностей и комбинаторные правила решения задач
Теория вероятностей и комбинаторные правила решения задач Уравнение прямой на координатной плоскости
Уравнение прямой на координатной плоскости Арифметикалық және геометриялық прогрессиялардың формулаларын пайдалана отырып есептер шығару
Арифметикалық және геометриялық прогрессиялардың формулаларын пайдалана отырып есептер шығару Методика профессионально ориентированного обучения: математика
Методика профессионально ориентированного обучения: математика Раскрытие скобок. 6 класс
Раскрытие скобок. 6 класс Теория вероятностей в задачах ЕГЭ
Теория вероятностей в задачах ЕГЭ Реализация деятельностного подхода на уроках математики.
Реализация деятельностного подхода на уроках математики. Математическая игра «Морской бой»
Математическая игра «Морской бой» Measures of variation. Week 4 (2)
Measures of variation. Week 4 (2) Таблица умножения на 3
Таблица умножения на 3 Обучение математике в рамках предпрофильного, профильного и углубленного обучения
Обучение математике в рамках предпрофильного, профильного и углубленного обучения Угол. Прямой и развернутый угол. Чертежный треугольник
Угол. Прямой и развернутый угол. Чертежный треугольник 5 класс математика
5 класс математика  Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Дифференциальные уравнения
Дифференциальные уравнения Математика. Логическая разминка
Математика. Логическая разминка Логика предикатов
Логика предикатов Элементы математической логики
Элементы математической логики Тренажер «Состав числа»
Тренажер «Состав числа» Решение уравнений (2 класс)
Решение уравнений (2 класс)