Содержание
- 2. Двойной интеграл Понятие двойного интеграла возникает при вычислении объёма цилиндрического бруса, подобно тому, как определённый интеграл
- 3. Где S ( dj) – площадь области dj . Если соответствует, независимо от выбора разбиения и
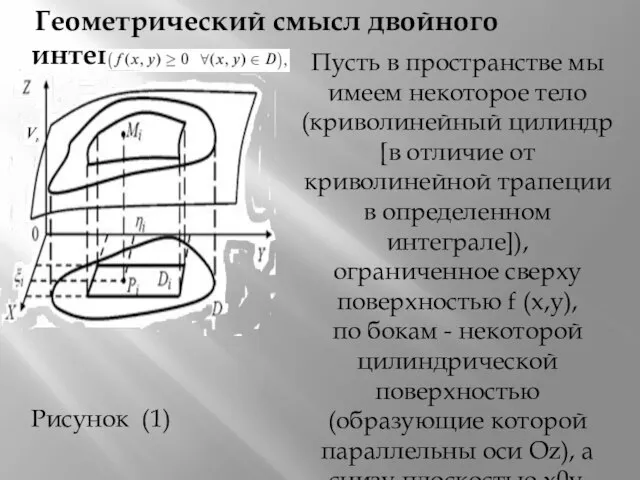
- 4. Геометрический смысл двойного интеграла Пусть в пространстве мы имеем некоторое тело (криволинейный цилиндр [в отличие от
- 5. СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА 1) Геометрический смысл двойного интеграла. Если f(x,y) – неотрицательна и интегрируема в области
- 6. 4) Двойной интеграл от алгебраической суммы двух (конечного числа) функций равен алгебраической сумме двойных интегралов от
- 7. 6) Если всюду в области (σ) f(x,y) > 0 (f(x,y) ≥ 0) , то 7) Если
- 8. 9) Теорема о среднем для двойного интеграла. Если функция f(x,y) непрерывна в замкнутой и ограниченной области
- 10. Вычисление двойного интеграла в д.с.к. Вычисление двойного интеграла сводится к повторному интегрированию. Пусть областью изменения независимых
- 11. Сначала вычисляется внутренний интеграл и в результате получаем некоторую функцию затем интегрируя её по другой переменной
- 12. Тогда соответствующий двойной интеграл: Замечание 3: Если область интегрирования не является правильной ни в одном из
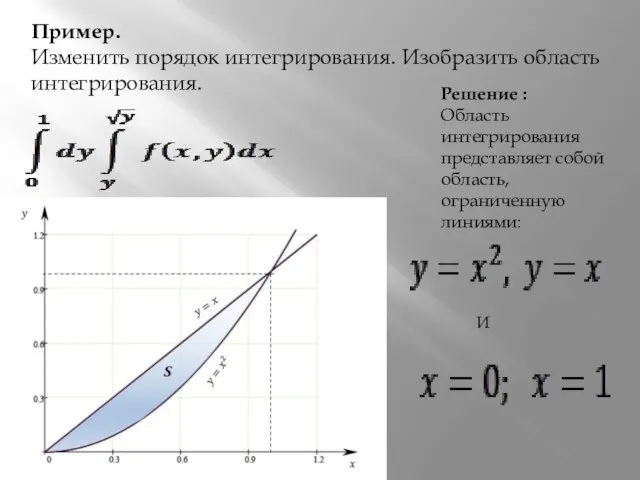
- 13. Пример. Изменить порядок интегрирования. Изобразить область интегрирования. Решение : Область интегрирования представляет собой область, ограниченную линиями:
- 14. Повторный интеграл с внешним интегрированием по Х :
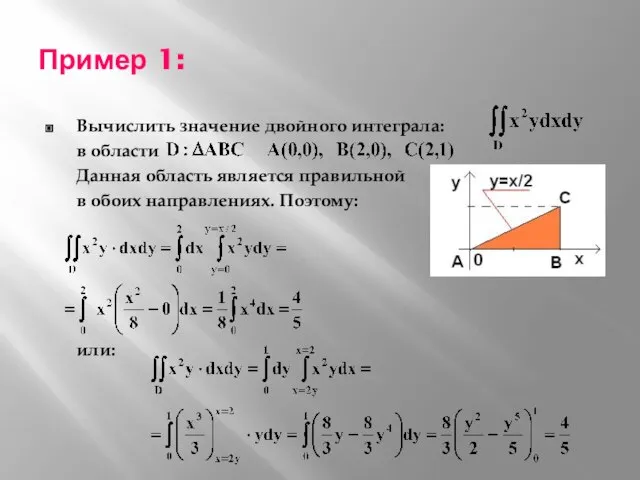
- 15. Пример 1: Вычислить значение двойного интеграла: в области Данная область является правильной в обоих направлениях. Поэтому:
- 16. Пример 2: Изменить порядок интегрирования в двойном интеграле: . Изобразим область интегрирования: Замечание: Пределы интегрирования необходимо
- 17. Пример 3: Не вычисляя двойного интеграла, выяснить, который из них имеет большее значение: Где область D
- 18. Пример 4. Найти где S — квадрат Расставляя пределы интегрирования, будем иметь Геометрически I представляет собой
- 20. Скачать презентацию














 Функції. Властивості функцій. Перетворення графіків функцій
Функції. Властивості функцій. Перетворення графіків функцій Морфрлогический анализ
Морфрлогический анализ тест по геометрии
тест по геометрии Измерение углов на местности
Измерение углов на местности Решение неравенств второй степени. Алгоритм решения
Решение неравенств второй степени. Алгоритм решения Решение уравнений и неравенств, содержащих переменную под знаком модуля
Решение уравнений и неравенств, содержащих переменную под знаком модуля Приглашаем в гости к Смешарикам
Приглашаем в гости к Смешарикам Теоретическая разминка. Десятичные дроби
Теоретическая разминка. Десятичные дроби Функция у=n квадратный корень из х, их свойства и графики
Функция у=n квадратный корень из х, их свойства и графики Симметрия в кубе, параллелепипеде, призме и пирамиде
Симметрия в кубе, параллелепипеде, призме и пирамиде Аксиомы стереомотрии
Аксиомы стереомотрии Ромб. Признаки ромба
Ромб. Признаки ромба Авторы: Авторы: Божина Г.Н. Застрогина О.М.
Авторы: Авторы: Божина Г.Н. Застрогина О.М. Сумма углов в треугольнике. Неравенство треугольника
Сумма углов в треугольнике. Неравенство треугольника РИСОВАНИЕ ФИГУР ОДНИМ РОСЧЕРКОМ. ГРАФЫ
РИСОВАНИЕ ФИГУР ОДНИМ РОСЧЕРКОМ. ГРАФЫ Тема урока: Координатная плоскость
Тема урока: Координатная плоскость Презентация на тему Королевство Дробей
Презентация на тему Королевство Дробей Корреляцияның параметрлік емес бағалау әдісі
Корреляцияның параметрлік емес бағалау әдісі Умножение и деление десятичных дробей
Умножение и деление десятичных дробей Аттестационная работа. Образовательная программа дополнительного образования «Пифагор»
Аттестационная работа. Образовательная программа дополнительного образования «Пифагор» Число и цифра 3
Число и цифра 3 Решение уравнений с одним неизвестным, сводящихся к линейным
Решение уравнений с одним неизвестным, сводящихся к линейным Таблица умножения и деления на 5
Таблица умножения и деления на 5 Вопрос и ответ Образцы и приёмы
Вопрос и ответ Образцы и приёмы Прямоугольный параллелепипед
Прямоугольный параллелепипед Интеграл. Урок обобщающего повторения
Интеграл. Урок обобщающего повторения Упрощение выражений (5 класс)
Упрощение выражений (5 класс) Электронный тренажёр по математике для учащихся 1 класса. Тема: «Материал для повторения и самоконтроля». ОС «Перспектива»
Электронный тренажёр по математике для учащихся 1 класса. Тема: «Материал для повторения и самоконтроля». ОС «Перспектива»