Содержание
- 2. и По условию функция y=f(x) дифференцируема в точке х0, следовательно ее предел при Переходим в этих
- 3. Геометрический смысл теоремы Ферма В точке наибольшего или наименьшего значения, достигаемого внутри промежутка Х, касательная к
- 4. Теорема Ролля Пусть функция y=f(x) удовлетворяет следующим условиям: Непрерывна на отрезке [a,b]. Дифференцируема на интервале (a,b).
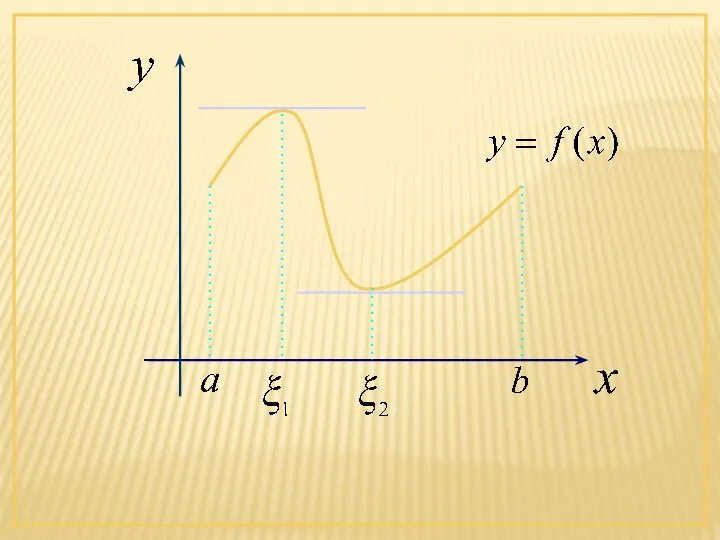
- 5. Геометрический смысл теоремы Ролля Найдется хотя бы одна точка, в которой касательная к графику функции параллельна
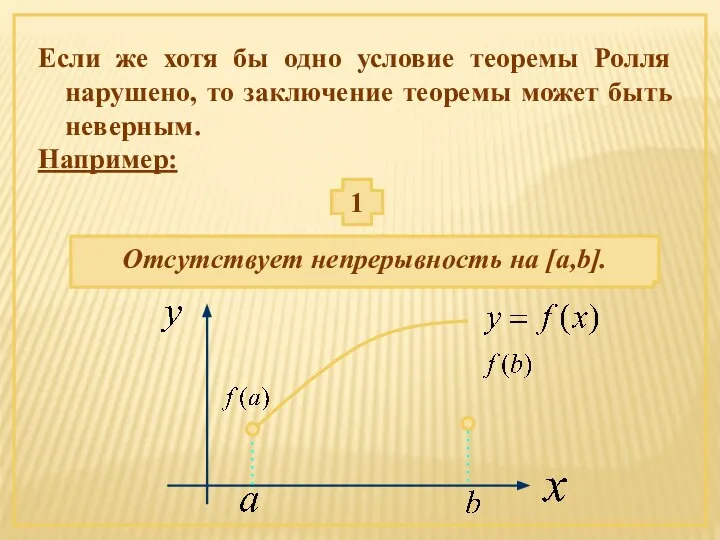
- 7. Если же хотя бы одно условие теоремы Ролля нарушено, то заключение теоремы может быть неверным. Например:
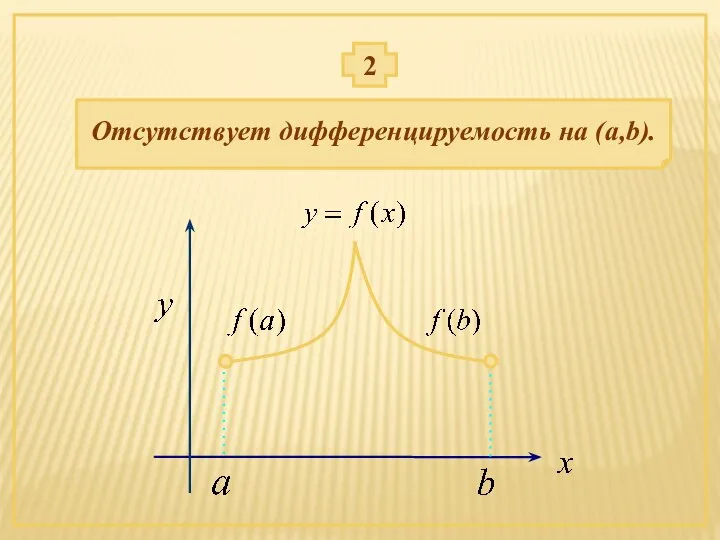
- 8. Отсутствует дифференцируемость на (a,b). 2
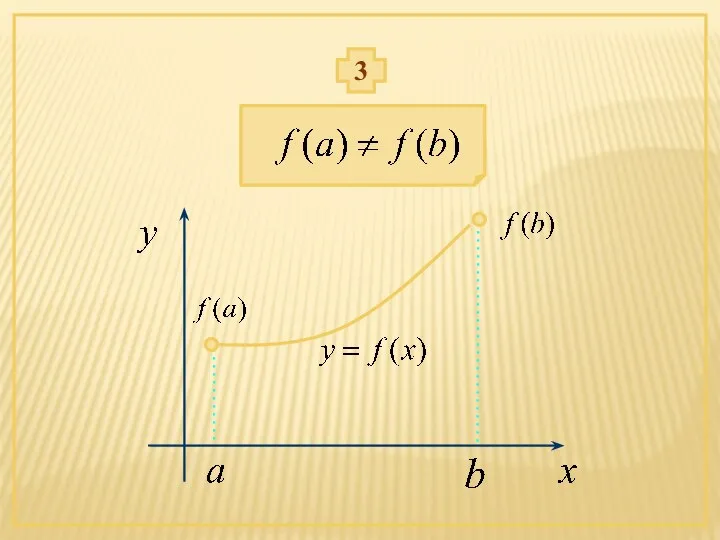
- 9. 3
- 10. Теорема Лагранжа Пусть функция y=f(x) удовлетворяет следующим условиям: Непрерывна на отрезке [a,b]. Дифференцируема на интервале (a,b).
- 11. Тогда внутри отрезка существует по крайней мере одна такая точка ξ, в которой производная функции равна
- 12. Эту теорему часто записывают в виде:
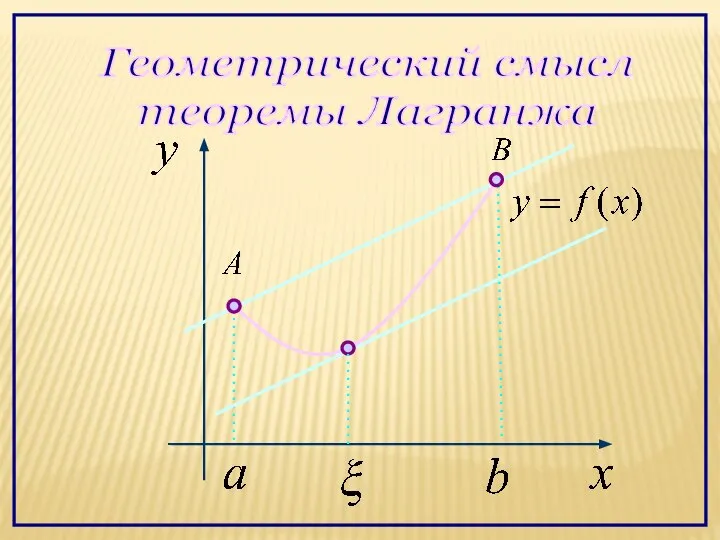
- 13. Геометрический смысл теоремы Лагранжа
- 14. Если перемещать прямую АВ параллельно начальному положению, то найдется хотя бы одна точка в которой касательная
- 15. Следствие. Если производная функции y=f(x) равна 0 на некотором промежутке Х, то эта функция постоянна на
- 16. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИЙ ТЕОРЕМА 1. (достаточное условие) возрастания функции) Если производная дифференцируемой функции положительна внутри
- 17. ТЕОРЕМА 2. (достаточное условие убывания функции) Если производная дифференцируемой функции отрицательна внутри некоторого промежутка Х, то
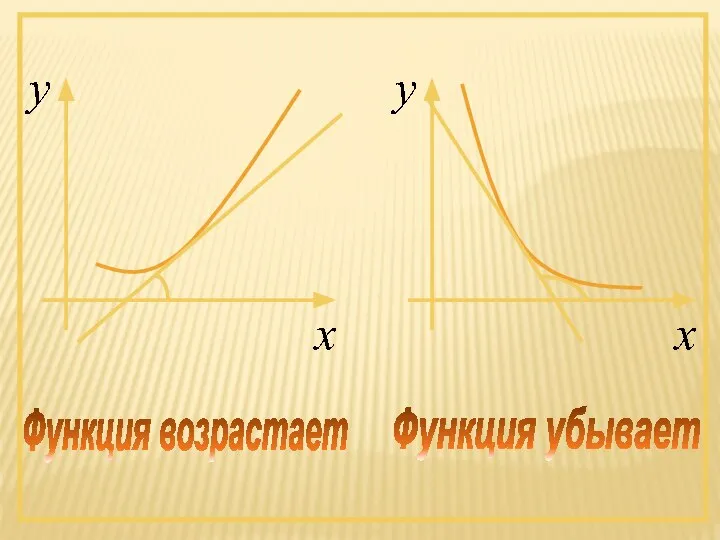
- 18. Геометрическая интерпретация Если касательные к кривой на некотором промежутке направлены под острыми углами к оси х,
- 19. Функция возрастает Функция убывает
- 20. Пример. Найти интервалы монотонности функции
- 21. Решение: Найдем производную этой функции: Исследуем знак этой производной: Следовательно, функция будет возрастать на промежутке Функция
- 22. ЭКСТРЕМУМ ФУНКЦИИ Точка х0 называется точкой максимума функции f(x), если в некоторой окрестности точки х0 выполняется
- 23. Точка х1 называется точкой минимума функции f(x), если в некоторой окрестности точки х1 выполняется неравенство Значения
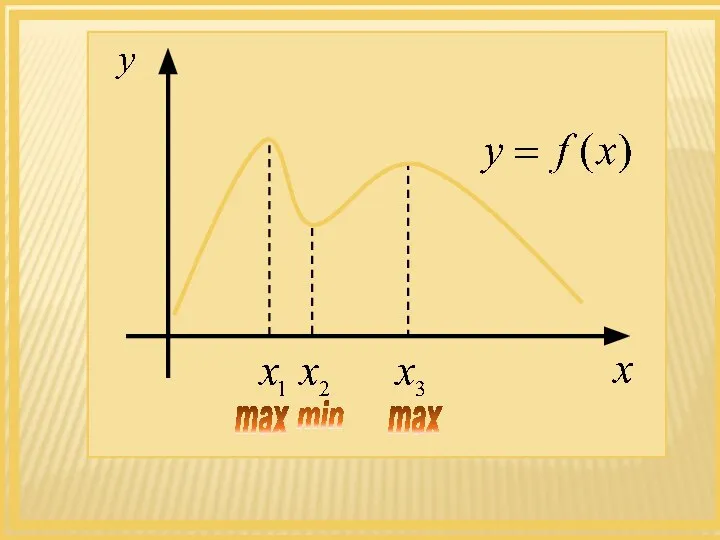
- 24. max min max
- 25. На одном промежутке функция может иметь несколько экстремумов, причем может быть, что минимум в одной точке
- 26. Для того, чтобы функция y=f(x) имела экстремум в точке х0 , необходимо, чтобы ее производная в
- 27. Точки, в которых выполняется необходимое условие экстремума, называются критическими или стационарными. Т.об., если в какой-либо точке
- 28. Найти критические точки и экстремумы функций: 1 Примеры
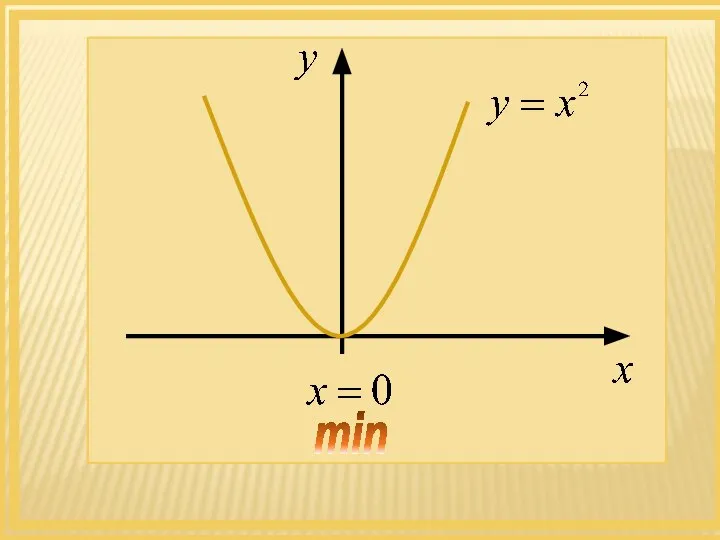
- 29. Решение: Применим необходимое условие экстремума: - критическая точка
- 30. min
- 31. 2
- 32. Решение: Применим необходимое условие экстремума: - критическая точка
- 34. Если при переходе через точку х0 производная дифференцируемой функции y=f(x)меняет знак с плюса на минус, то
- 35. 1 Найти производную функции 2 Найти критические точки функции, в которых производная равна нулю или не
- 36. 3 Исследовать знак производной слева и справа от каждой критической точки. 4 Найти экстремум функции.
- 37. Исследовать функцию на экстремум: Пример
- 38. Решение: Применим схему исследования функции на экстремум: 1 Находим производную функции:
- 39. 2 Находим критические точки: критические точки
- 40. 3 Исследуем знак производной слева и справа от каждой критической точки: min В точке х=1 экстремума
- 41. 4 Находим экстремум функции:
- 42. Если первая производная дифференцируемой функции y=f(x) в точке х0 равна нулю, а вторая производная в этой
- 43. Схема исследования функции на экстремум в этом случае аналогична предыдущей, но третий пункт следует заменить на:
- 44. Из второго достаточного условия следует, что если в критической точке вторая производная функции не равна нулю,
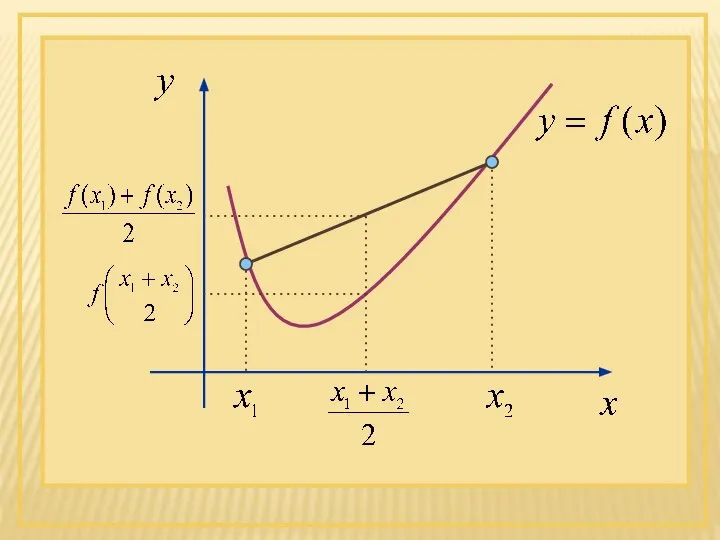
- 45. ВЫПУКЛОСТЬ ФУНКЦИИ. ТОЧКИ ПЕРЕГИБА. Функция y=f(x) называется выпуклой вниз (вогнутой) на промежутке Х, если для любых
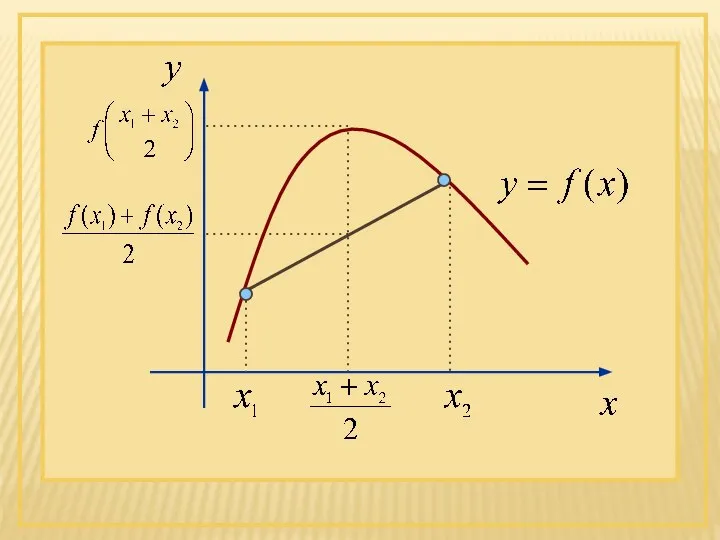
- 47. Функция y=f(x) называется выпуклой вверх на промежутке Х, если для любых х1, х2 из этого промежутка
- 49. ТЕОРЕМА 1. Функция выпукла вверх (вниз) на промежутке Х тогда и только тогда, когда ее первая
- 50. ТЕОРЕМА 2. достаточное условие выпуклости функции Если вторая производная дифференцируемой функции положительна (отрицательна) на некотором промежутке
- 51. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, на которых функция выпукла вверх и вниз.
- 52. ТЕОРЕМА 3. необходимое условие перегиба Вторая производная дифференцируемой функции в точке перегиба х0 равна нулю:
- 53. ТЕОРЕМА 4. достаточное условие перегиба Если вторая производная дифференцируемой функции в точке х0 меняет свой знак,
- 54. схема исследования функции на выпуклость и точки перегиба: 1 Найти вторую производную функции. 2 Найти точки,
- 55. 3 Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах
- 56. Пример. Найти интервалы выпуклости и точки перегиба функции
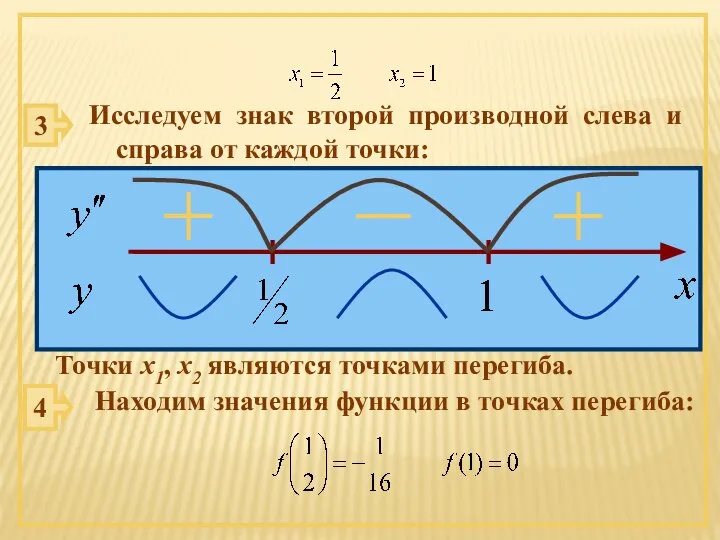
- 57. Решение: 1 Находим вторую производную: 2 Находим точки, в которых вторая производная обращается в нуль:
- 58. 3 Исследуем знак второй производной слева и справа от каждой точки: Точки х1, х2 являются точками
- 59. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ Асимптотой графика функции y=f(x) называется прямая, такая что расстояние от точки (x,f(x)) до
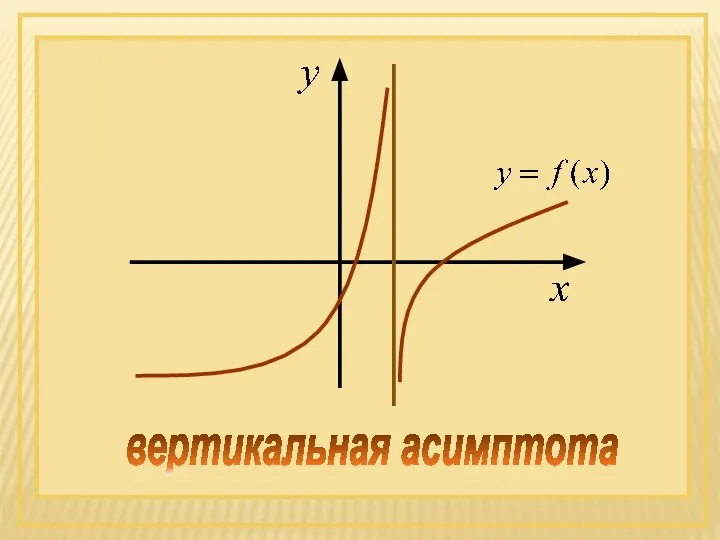
- 60. вертикальная асимптота
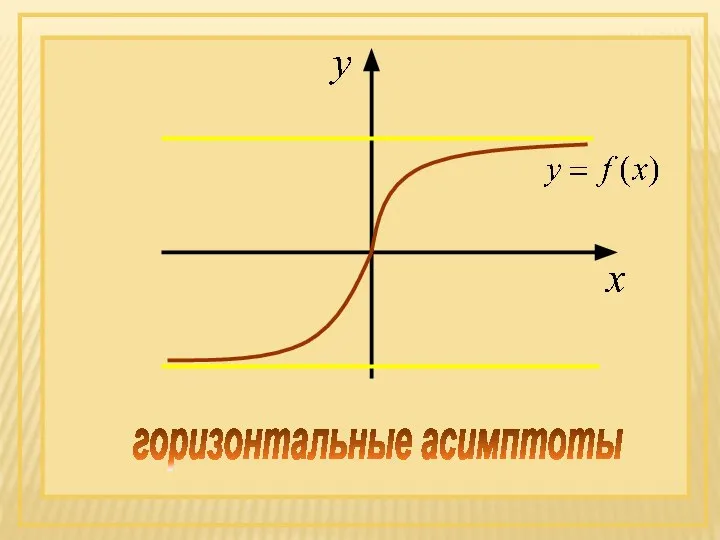
- 61. горизонтальные асимптоты
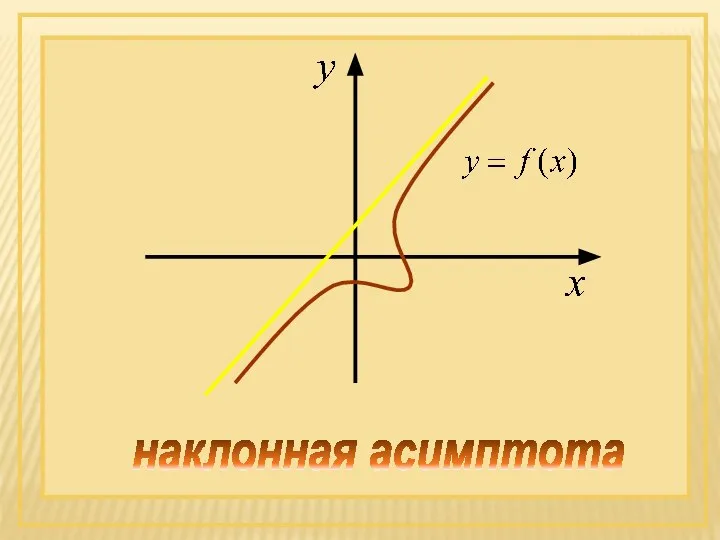
- 62. наклонная асимптота
- 63. ТЕОРЕМА 1. Пусть функция y=f(x) определена в некоторой окрестности точки х0 (исключая, может быть, саму эту
- 64. Тогда прямая х=х0 является вертикальной асимптотой графика функции y=f(x). или
- 65. Очевидно, что прямая х=х0 не может быть вертикальной асимптотой, если функция непрерывна в точке х0, т.к.
- 66. ТЕОРЕМА 2. Пусть функция y=f(x) определена при достаточно больших х и существует конечный предел функции Тогда
- 67. ТЕОРЕМА 3. Пусть функция y=f(x) определена при достаточно больших х и существуют конечные пределы Тогда прямая
- 68. Пример. Найти асимптоты графика функции
- 69. Решение: Функция не имеет точек разрыва, следовательно вертикальных асимптот у нее нет. 1 2 Найдем горизонтальные
- 70. Следовательно, прямая является наклонной асимптотой.
- 71. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ 1 Найти область определения функции. 2 Исследовать функцию на четность
- 72. 3 Найти вертикальные асимптоты. 4 Исследовать поведение функции на бесконечности и найти горизонтальные или наклонные асимптоты.
- 73. 6 Найти интервалы выпуклости функции и точки перегиба. 7 Найти точки пересечения графика с осями координат
- 74. Пример. Исследовать функцию и построить ее график
- 75. Решение: 1 Находим область определения функции. Функция определена при всех значениях х, кроме Следовательно, область определения
- 76. Функция является четной, следовательно ее график будет симметричен относительно оси ординат. Функция не периодична. 3 Находим
- 77. При слева При справа Следовательно, прямая х=1 является вертикальной асимптотой. Аналогично можно проанализировать х=-1, но так
- 78. Следовательно, y=-1 - горизонтальная асимптота. Т.к. то наклонных асимптот нет. 5 Найдем интервалы монотонности и экстремумы
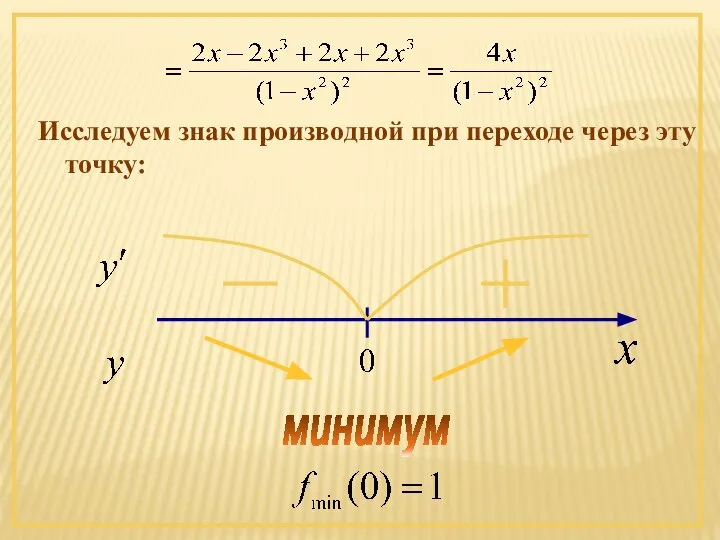
- 79. Исследуем знак производной при переходе через эту точку: минимум
- 80. Интервалы монотонности функции: Функция убывает на: Функция возрастает на: 6 Найдем интервалы выпуклости и точки перегиба.
- 81. Точек, в которых вторая производная обращается в ноль, нет. Поэтому точек перегиба у графика нет. Числитель
- 82. Интервалы выпуклости функции: Функция выпукла вниз на: Функция выпукла вверх на: 7 Найдем точки пересечения графика
- 84. Скачать презентацию




![Теорема Лагранжа Пусть функция y=f(x) удовлетворяет следующим условиям: Непрерывна на отрезке [a,b]. Дифференцируема на интервале (a,b).](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/732861/slide-9.jpg)





























































 Презентация по математике "Десятичная система и двоичная" - скачать бесплатно
Презентация по математике "Десятичная система и двоичная" - скачать бесплатно Делимость чисел
Делимость чисел Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Числові нерівності. Властивості числових нерівностей
Числові нерівності. Властивості числових нерівностей Сложение чисел с разными знаками
Сложение чисел с разными знаками Симметрия. Г. Вейль – немецкий математик
Симметрия. Г. Вейль – немецкий математик Лесная биометрия
Лесная биометрия Построение сечения
Построение сечения Тени основных геометрических фигур (по одной проекции)
Тени основных геометрических фигур (по одной проекции) Умножение на двухзначное число
Умножение на двухзначное число ВКР: Исследование нормального строения конечных групп
ВКР: Исследование нормального строения конечных групп Учитель Вавилкина Г.Н. Глубоковская ООШ
Учитель Вавилкина Г.Н. Глубоковская ООШ Решение задач на смеси и растворы с помощью уравнений
Решение задач на смеси и растворы с помощью уравнений Зачем мы изучаем алгебру?
Зачем мы изучаем алгебру? перпендикулярность прямой и плоскости
перпендикулярность прямой и плоскости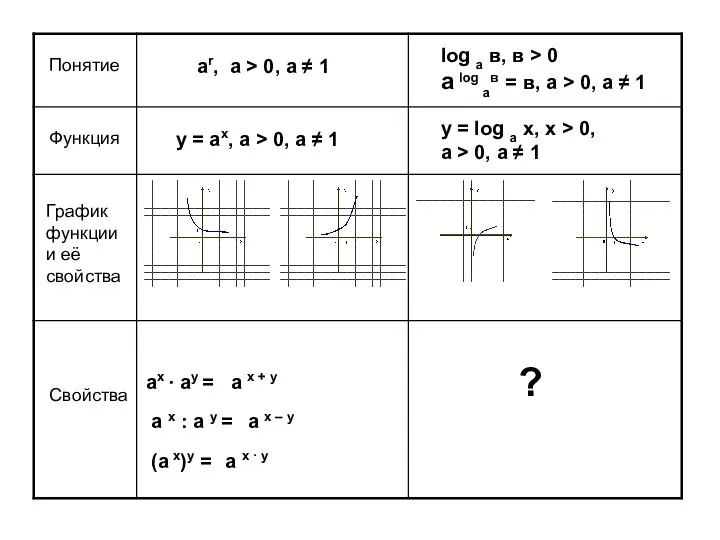 Свойства логарифмов
Свойства логарифмов Весёлый счет
Весёлый счет Урок правильные многогранники (наглядная геометрия)
Урок правильные многогранники (наглядная геометрия) Обзор методов оценки профессиональных рисков
Обзор методов оценки профессиональных рисков Презентация по математике Действия с десятичными дробями
Презентация по математике Действия с десятичными дробями  Задачи с величинами: цена, количество, стоимость
Задачи с величинами: цена, количество, стоимость Задача на тему: Прогрессия
Задача на тему: Прогрессия Пирамида, вписанная в конус
Пирамида, вписанная в конус Комбинаторные методы решения вероятностных задач
Комбинаторные методы решения вероятностных задач Тригонометрия. (Лекция 2)
Тригонометрия. (Лекция 2) Фалес: Познать себя трудно, советовать другим легко
Фалес: Познать себя трудно, советовать другим легко Решение треугольников
Решение треугольников