Содержание
- 2. Импликацией предикатов А(х) и В(х), заданных на множестве Х, называется предикат А(х)⇒В(х), заданный на том же
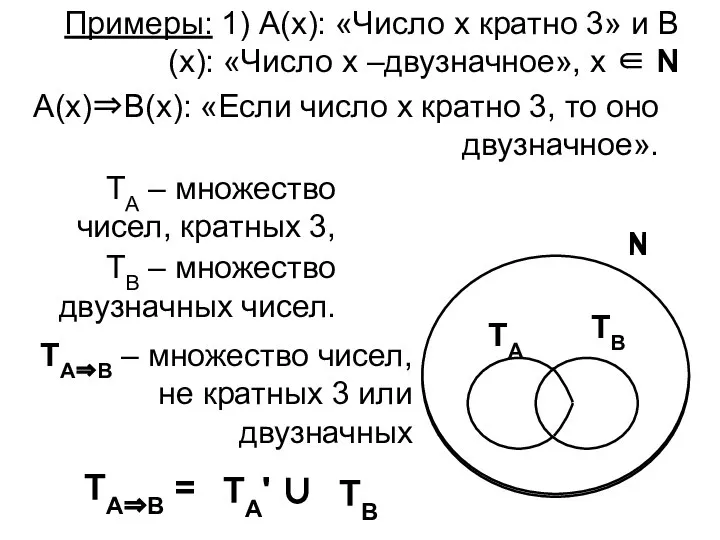
- 3. Примеры: 1) А(х): «Число х кратно 3» и В(х): «Число х –двузначное», х ∈ N А(х)⇒В(х):
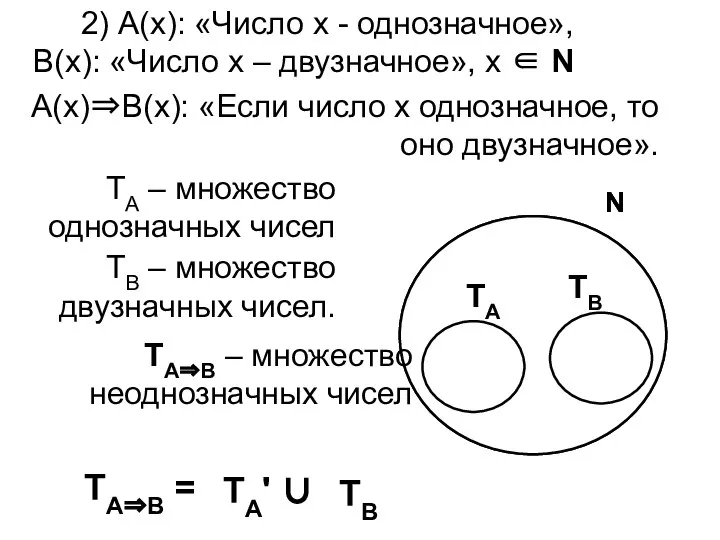
- 4. 2) А(х): «Число х - однозначное», В(х): «Число х – двузначное», х ∈ N А(х)⇒В(х): «Если
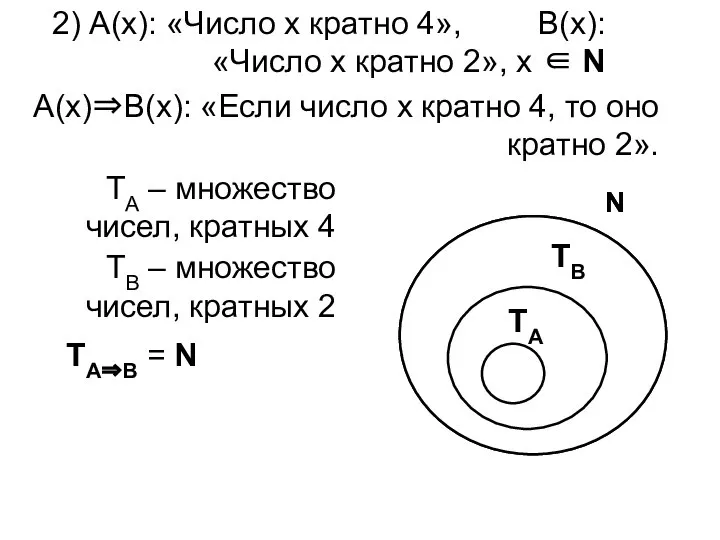
- 5. 2) А(х): «Число х кратно 4», В(х): «Число х кратно 2», х ∈ N А(х)⇒В(х): «Если
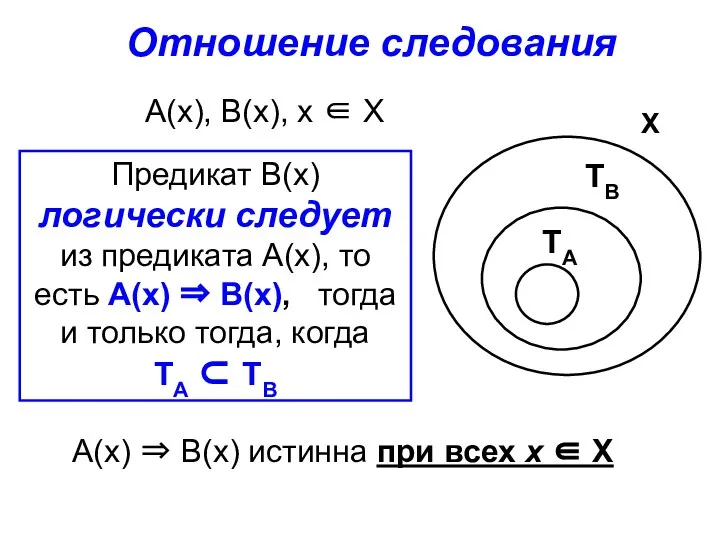
- 6. Отношение следования А(х), В(х), х ∈ Х А(х) ⇒ В(х) истинна при всех х ∈ Х
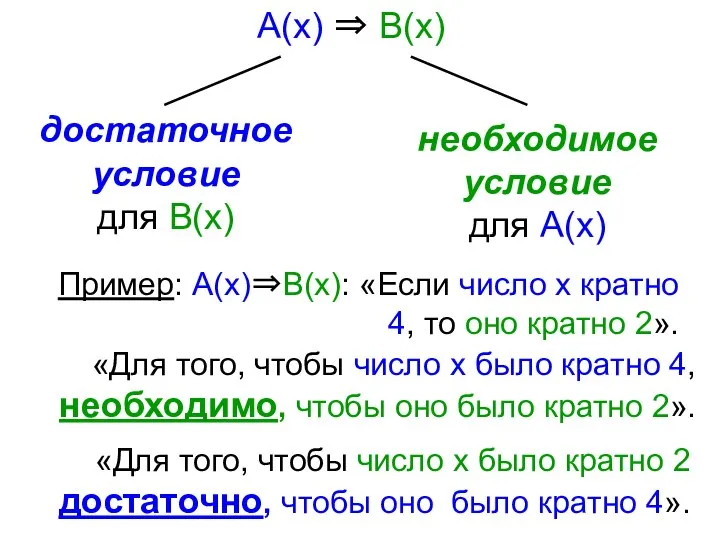
- 7. Пример: А(х)⇒В(х): «Если число х кратно 4, то оно кратно 2». «Для того, чтобы число х
- 8. Эквиваленцией предикатов А(х) и В(х), заданных на множестве Х, называется предикат А(х)⇔В(х), заданный на том же
- 9. Если предикаты А(х) и В(х) равносильны на множестве Х, то эквиваленция предикатов А(х) ⇔ В(х) истинна
- 10. Пример: А(х) «Число х делится на 10», В(х): «Запись числа х заканчивается цифрой 0» А(х)⇔В(х): «Число
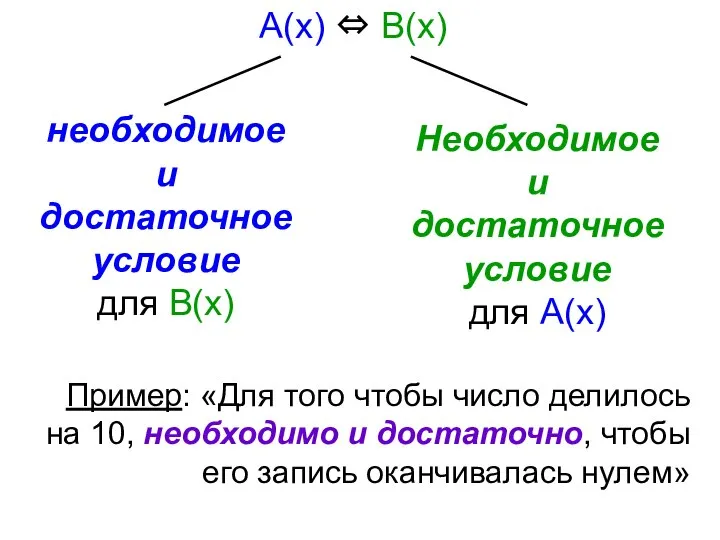
- 11. Пример: «Для того чтобы число делилось на 10, необходимо и достаточно, чтобы его запись оканчивалась нулем»
- 12. Замечание. Из равносильности предикатов А(х) и В(х) на некотором множестве Х не следует, что предикаты, выраженные
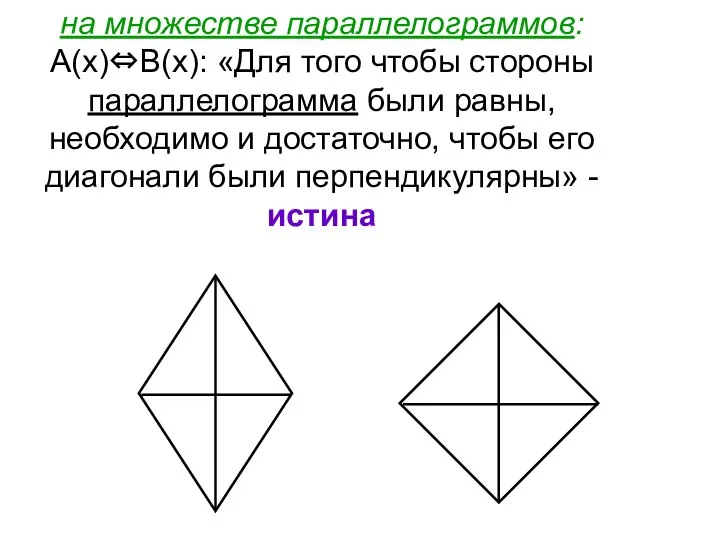
- 13. на множестве параллелограммов: А(х)⇔В(х): «Для того чтобы стороны параллелограмма были равны, необходимо и достаточно, чтобы его
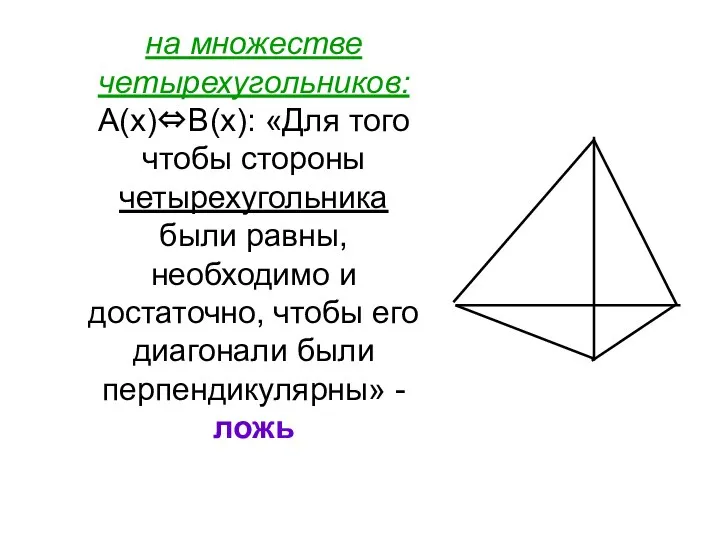
- 14. на множестве четырехугольников: А(х)⇔В(х): «Для того чтобы стороны четырехугольника были равны, необходимо и достаточно, чтобы его
- 15. Теоремы
- 16. Теорема – это высказывание, истинность которого устанавливается посредством рассуждения (доказательства). Теорема - от греч. τεορεμα -
- 17. С логической точки зрения теорема представляет собой высказывание А(х) ⇒ В(х), где А(х) и В(х) –
- 18. Пример: «В прямоугольнике диагонали равны». Если четырехугольник является прямоугольником, то диагонали в нем равны Из того,
- 19. Кроме условия и заключения теорема содержит разъяснительную часть (словесно она обычно не формулируется, но всегда подразумевается,
- 20. В математике кроме теорем используются предложения, называемые правилами и формулами. Пример: правило деления суммы на число:
- 21. А(х) ⇒ В(х) – данная теорема В(х) ⇒ А(х) - теорема обратная данной - теорема противоположная
- 22. А(х) ⇒ В(х): «Если сумма цифр числа кратна 9, то и само число кратно 9» В(х)
- 24. Замечание. Если условие или заключение данной теоремы представляет собой конъюнкцию или дизъюнкцию, то чтобы получить теорему
- 25. ПРИМЕР: А(х) ⇒ В(х): «ЕСЛИ ЧИСЛО ДЕЛИТСЯ НА 3 И НА 5, ТО ОНО ДЕЛИТСЯ НА
- 26. Если для данной теоремы А(х) ⇒ В(х) истинна обратная теорема В(х) ⇒ А(х), то их можно
- 27. Пример: А(х) ⇒ В(х): «В равнобедренном треугольнике углы при основании равны» В(х) ⇒ А(х): «Если в
- 28. А(х) ⇔ В(х): «Для того, чтобы треугольник был равнобедренным, необходимо и достаточно, чтобы в нем углы
- 29. ЕСЛИ ТЕОРЕМА ИМЕЕТ ВИД РАВНОСИЛЬНОСТИ А(Х) ⇔ В(Х), ТО ЭТО ЗНАЧИТ, ЧТО ОНА СОСТОИТ ИЗ ДВУХ
- 30. Упражнения: Выделите условие и заключение в каждой из следующих теорем: а) Диагонали прямоугольника равны. б) Равенство
- 32. Скачать презентацию




















 Проверка статистических гипотез
Проверка статистических гипотез Теория в области нечеткой логики и нечеткого множества
Теория в области нечеткой логики и нечеткого множества Формирование познавательного интереса школьников к учению на уроках математики
Формирование познавательного интереса школьников к учению на уроках математики Основы теории нечетких множеств
Основы теории нечетких множеств Рационал сандарды қорытындылау
Рационал сандарды қорытындылау Смежные и вертикальные углы. Задачи
Смежные и вертикальные углы. Задачи Деление с остатком
Деление с остатком Матрицы. Определители и их свойства (лекция № 1)
Матрицы. Определители и их свойства (лекция № 1) Активизация мыслительной деятельности учащихся на уроках математики
Активизация мыслительной деятельности учащихся на уроках математики Однородное уравнение повышенной сложности
Однородное уравнение повышенной сложности Квадратные уравнения. Повторение. 8 класс
Квадратные уравнения. Повторение. 8 класс История возникновения геометрии как науки
История возникновения геометрии как науки Решение задач с помощью уравнений. Устные вычисления
Решение задач с помощью уравнений. Устные вычисления Множества. Эквивалентные множества
Множества. Эквивалентные множества Презентация на тему Приведение дробей к общему знаменателю (урок в 6 классе)
Презентация на тему Приведение дробей к общему знаменателю (урок в 6 классе) Тригонометрические формулы. Диктант
Тригонометрические формулы. Диктант Параллельные прямые
Параллельные прямые Линии второго порядка
Линии второго порядка Математический аукцион (6 класс)
Математический аукцион (6 класс) Треугольник. Медиана, биссектриса, высота. Первый признак равенства треугольников
Треугольник. Медиана, биссектриса, высота. Первый признак равенства треугольников Сложение и вычитание многозначных чисел. Алгоритм письменного вычисления
Сложение и вычитание многозначных чисел. Алгоритм письменного вычисления Решение рациональных уравнений
Решение рациональных уравнений Свойства квадарата
Свойства квадарата Презентация по математике "Путешествие в мир чисел" - скачать
Презентация по математике "Путешествие в мир чисел" - скачать  Фалес Милетский - один из первых геометров
Фалес Милетский - один из первых геометров "Веселый счет" (овощи)
"Веселый счет" (овощи) Численное решение обыкновенных дифференциальных уравнений
Численное решение обыкновенных дифференциальных уравнений Метод вспомогательной окружности
Метод вспомогательной окружности