Содержание
- 2. Модель парной линейной регрессии Коэффициент корреляции показывает, что две переменные связаны друг с другом, однако он
- 3. Начнем с простейшей модели - модели парной линейной регрессии: y = α+βx+u.
- 4. Величина y, рассматриваемая как зависимая переменная, состоит из двух составляющих: неслучайной составляющей α+βx, где x выступает
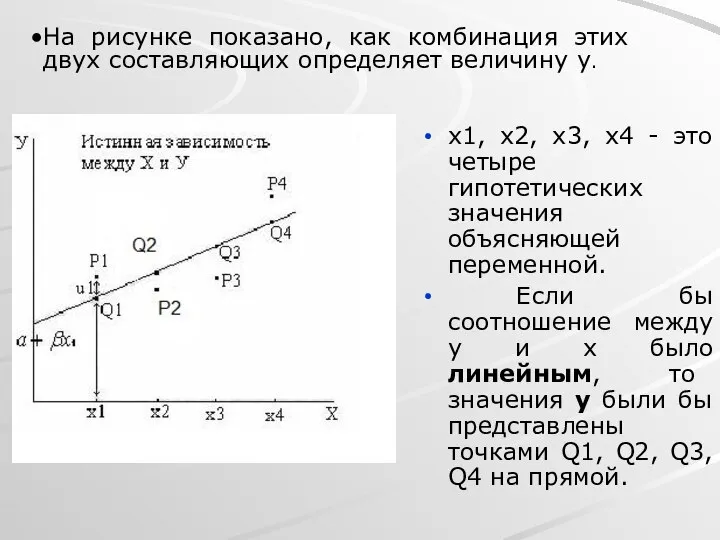
- 5. x1, x2, x3, x4 - это четыре гипотетических значения объясняющей переменной. Если бы соотношение между y
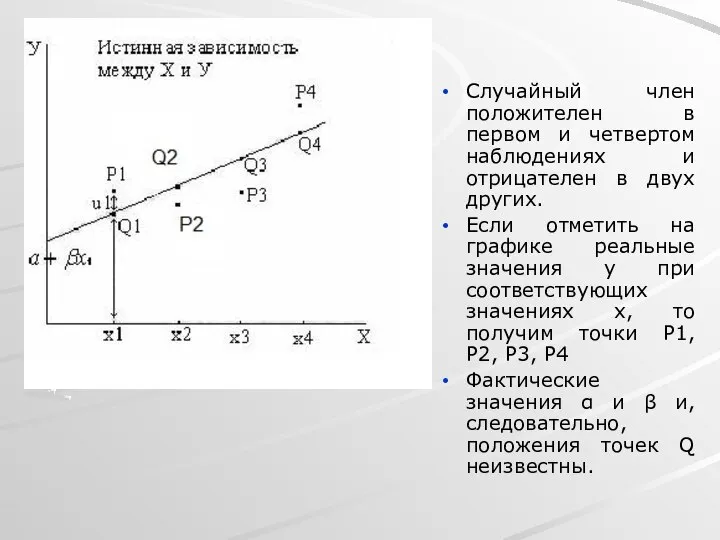
- 6. Случайный член положителен в первом и четвертом наблюдениях и отрицателен в двух других. Если отметить на
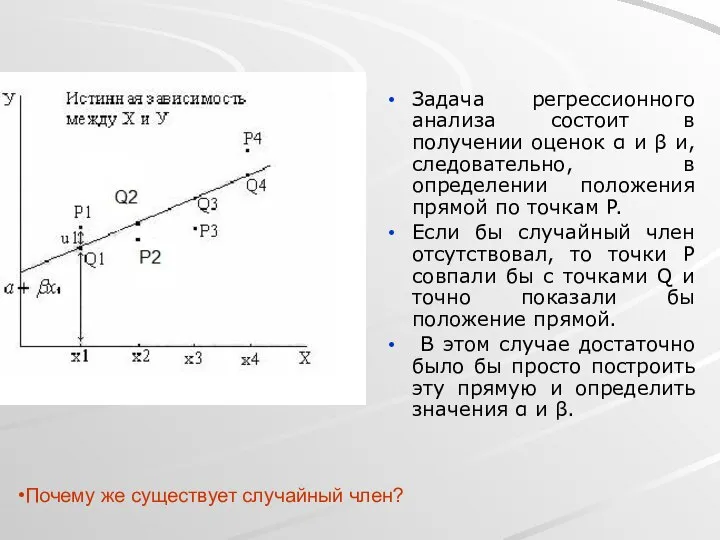
- 7. Задача регрессионного анализа состоит в получении оценок α и β и, следовательно, в определении положения прямой
- 8. Причины существования случайного члена 1. Невключение объясняющих переменных. Соотношения между y и x является большим упрощением.
- 9. Часто происходит так, что имеются переменные, которые мы хотели бы включить в регрессионное уравнение, но не
- 10. Кроме того, могут быть факторы, которые являются существенными, но которые мы из-за отсутствия опыта таковыми не
- 11. 2. Агрегирование переменных. Во многих случаях рассматриваемая зависимость - это попытка объединить вместе некоторое число микроэкономических
- 12. 3. Неправильное описание структуры модели. Структура модели может быть описана неправильно или не вполне правильно. Например,
- 13. 4. Неправильная функциональная спецификация. Функциональное соотношение между y и x математически может быть определено неправильно. Например,
- 14. Ошибки измерения. Если в измерении одной или более взаимосвязанных переменных имеются ошибки, то наблюдаемые значения не
- 15. Регрессия по методу наименьший квадратов. Допустим, имеется четыре наблюдения для x и y, и поставлена задача
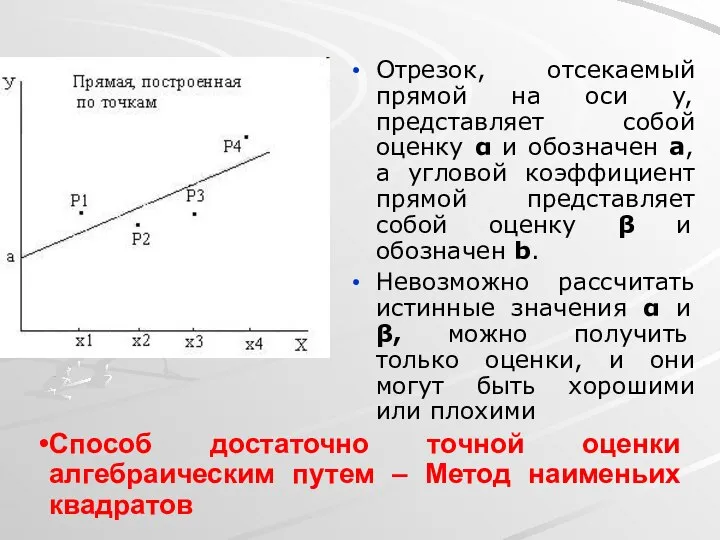
- 16. Отрезок, отсекаемый прямой на оси y, представляет собой оценку α и обозначен a, а угловой коэффициент
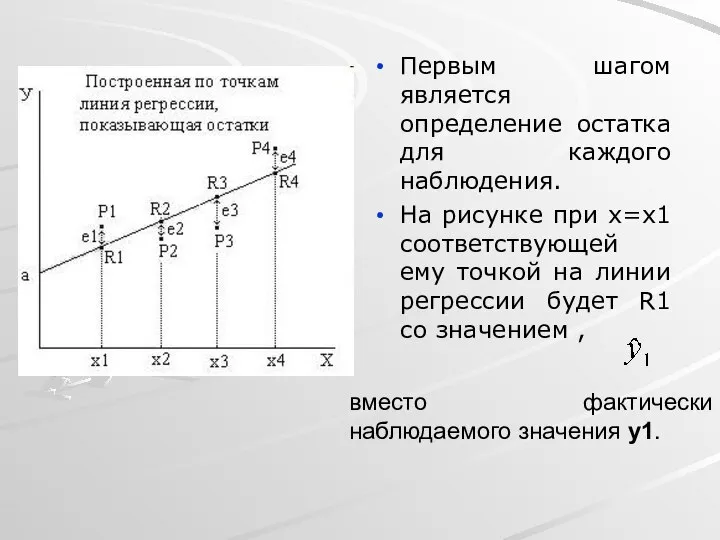
- 17. Первым шагом является определение остатка для каждого наблюдения. На рисунке при х=x1 соответствующей ему точкой на
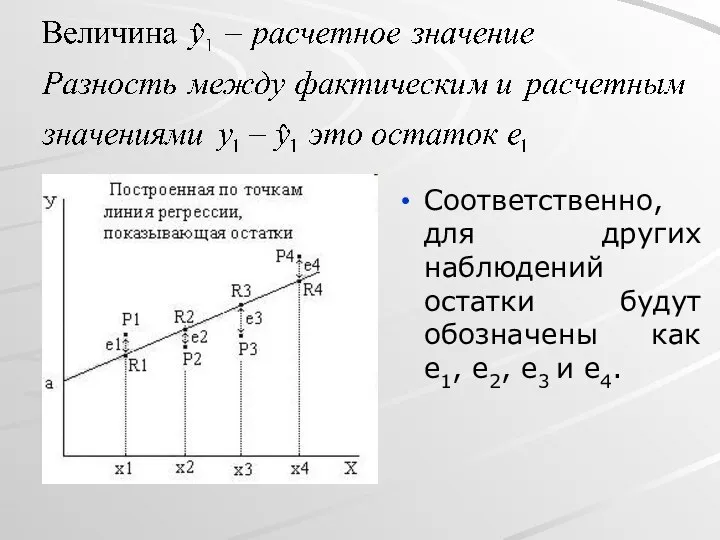
- 18. Соответственно, для других наблюдений остатки будут обозначены как e1, e2, e3 и e4.
- 19. Очевидно, что мы хотим построить линию регрессии таким образом, чтобы остатки были минимальными. Очевидно также, что
- 20. Одним из способов решения поставленной проблемы состоит в минимизации суммы квадратов остатков S — метод наименьших
- 21. Величина S будет зависеть от выбора a и b, так как они определяют положение линии регрессии.
- 22. Рассмотрим случай, когда имеется n наблюдений двух переменных x и y. Предположив, что y зависит от
- 23. Вывод выражений для a и b Выразим квадрат i-го остатка через a и b и наблюдения
- 24. Мы можем влиять на величину S, только задавая a и b. Значения x и y, которые
- 25. Первое уравнение позволяет выразить a Следовательно
- 26. Подставив выраженное a во второе уравнение, затем поделив на 2n и перегруппировав, получим: bVar(x)=Cov(x,y), и таким
- 27. Существуют и другие достаточно разумные решения, однако при выполнении определенных условий метод наименьших квадратов дает несмещенные
- 28. Качество оценки: коэффициент детерминации R2 Цель регрессивного анализа состоит в объяснении поведения зависимой переменной y. В
- 29. В парном регрессионном анализе мы пытаемся объяснить поведение y путем определения регрессионной зависимости y от соответственно
- 30. Это то значение, которое имел бы y при условии, что уравнение регрессии было бы правильным, и
- 31. Значит мы можем разложить Var(y) на две части и Var(e) - "необъяснимую" часть.
- 32. Это коэффициент детерминации Максимальное значение коэффициента R2 равно единице. Это происходит в том случае, когда линия
- 33. Если в выборке отсутствует видимая связь между y и x, то коэффициент R2 будет близок к
- 34. Принцип минимизации суммы квадратов остатков эквивалентен минимизации дисперсии остатков. Однако, если мы минимизируем Var(e), то при
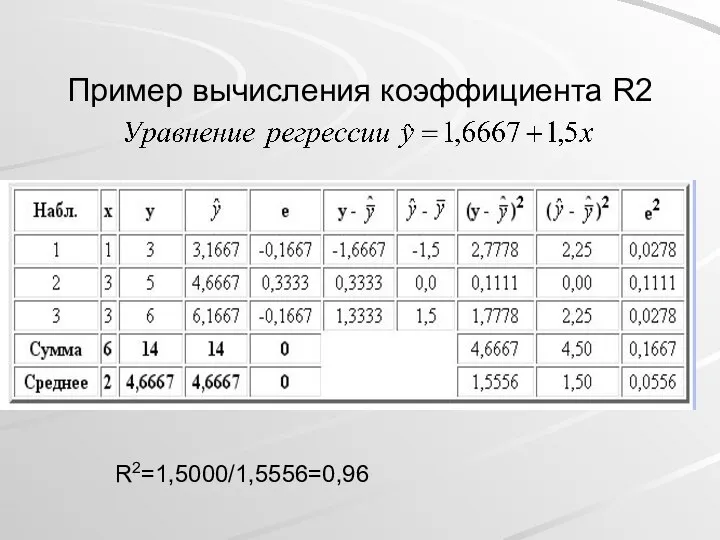
- 35. Пример вычисления коэффициента R2 R2=1,5000/1,5556=0,96
- 36. Общая сумма квадратов TSS – сумма квадратов отклонений y от своего среднего значения Объясненная сумма квадратов
- 37. Другая формула для коэффициента детерминации
- 38. То есть коэффициент детерминации равен квадрату выборочной корреляции между y и a+bx Связь между коэффициентом детерминации
- 40. Скачать презентацию






























 Реєстрація осіб для участі в зовнішньому незалежному оцінюванні
Реєстрація осіб для участі в зовнішньому незалежному оцінюванні Использование циклов
Использование циклов Трапеция. Свойства трапеции. Геометрия, 7 класс
Трапеция. Свойства трапеции. Геометрия, 7 класс Тренировочная работа №5 2019-2020. Вариант 1
Тренировочная работа №5 2019-2020. Вариант 1 Приёмы письменных вычислений (3 класс)
Приёмы письменных вычислений (3 класс) Вовка в тридевятом царстве
Вовка в тридевятом царстве Параллельность прямых и плоскостей в пространстве
Параллельность прямых и плоскостей в пространстве Метрические пространства
Метрические пространства Презентация по математике "Круг Эйлера" - скачать
Презентация по математике "Круг Эйлера" - скачать  Отношения и пропорции
Отношения и пропорции Отношение эквивалентности и фактор-множество
Отношение эквивалентности и фактор-множество Линейные неравенства. Системы линейных неравенств. Повторение
Линейные неравенства. Системы линейных неравенств. Повторение Задачи на совместную работу. 5 класс
Задачи на совместную работу. 5 класс Визначення часу за годинником. Хвилини. Розв’язування вправ і задач на засвоєння вивчення таблиць множення і ділення
Визначення часу за годинником. Хвилини. Розв’язування вправ і задач на засвоєння вивчення таблиць множення і ділення Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Презентация на тему Решение задач с помощью уравнений 7 КЛАСС
Презентация на тему Решение задач с помощью уравнений 7 КЛАСС  Системы счисления. Все есть число
Системы счисления. Все есть число Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа Математические модели управления
Математические модели управления Симметрия в геометрии
Симметрия в геометрии Бесплатный интенсив по тригонометрии
Бесплатный интенсив по тригонометрии Неопределённый интегра́л Выполнил: Студент группы К-11 ХК ДУТ Божко Павел
Неопределённый интегра́л Выполнил: Студент группы К-11 ХК ДУТ Божко Павел  Одночлен и его стандартный вид
Одночлен и его стандартный вид Демакова Ирина Павловна - учитель математики МБОУ «Лицей №1» г. Норильска
Демакова Ирина Павловна - учитель математики МБОУ «Лицей №1» г. Норильска  Десятичные дроби. Что мы знаем о них?
Десятичные дроби. Что мы знаем о них?  Координатная плоскость
Координатная плоскость Франсуа Виет и его теорема
Франсуа Виет и его теорема Өмір сүруді талдау
Өмір сүруді талдау