Содержание
- 2. Перестановки Перестановкой порядка N называется расположение N различных объектов в ряд в некотором порядке. Например, для
- 3. Инверсии Пусть даны базовое множество из N элементов 1,2, 3,..., N и его перестановка Пара называется
- 4. Таблицей инверсий перестановки a1,a2, ...,aN называется последовательность чисел b1, b2 …, bN , где bj есть
- 5. Построение перестановки по таблице инверсий 1 способ: проход по таблице инверсий справа налево Создается заготовка перестановки
- 6. Алгоритм П1: построение перестановки по таблице инверсий справа налево Вход: N > 0 - количество элементов
- 7. Построение перестановки по таблице инверсий 2 способ: проход по таблице инверсий слева направо Создается заготовка пустой
- 8. Алгоритм П2: построение перестановки по таблице инверсий слева направо Вход: N > 0 - количество элементов
- 9. Инверсионный метод поиска всех перестановок Таблица инверсий однозначно определяет перестановку и каждая перестановка имеет только одну
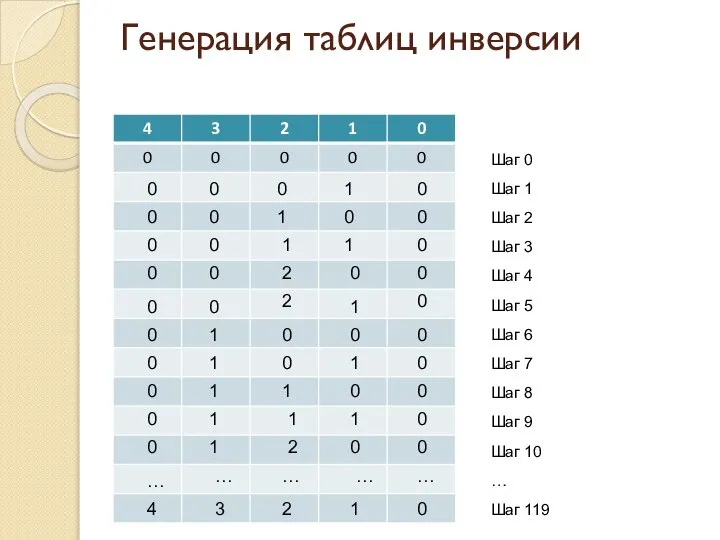
- 10. Генерация таблиц инверсии 0 0 0 0 0 0 0 0 0 1 1 1 …
- 11. Алгоритм И1: нахождение следующей таблицы инверсий Пусть B = b1, b2, ..., bN – таблица инверсий,
- 12. Алгоритм Дейкстры: поиск следующей по алфавиту перестановки Пусть даны две перестановки b = b1, b2 …,
- 13. Идея алгоритма Дейкстры: определить каким-либо образом функцию, которая по заданной перестановке выдает непосредственно следующую за ней
- 14. Алгоритм Дейкстры: генерация следующей по алфавиту перестановки Вход: N > 0 — количество элементов; a1, a2,
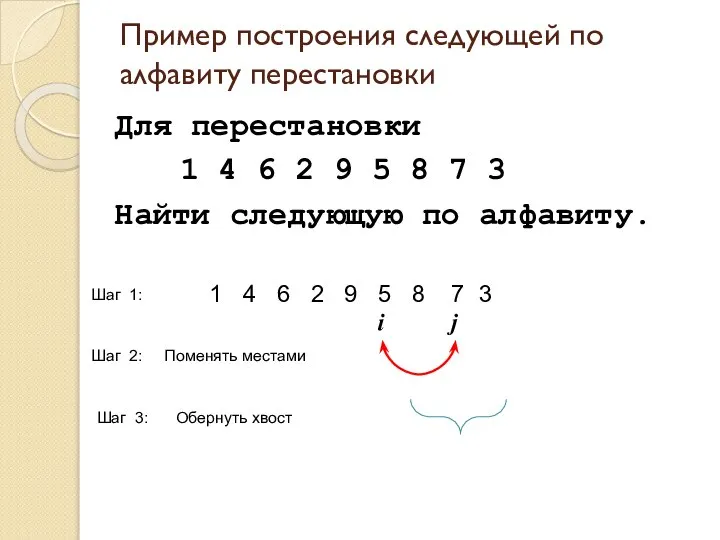
- 15. Пример построения следующей по алфавиту перестановки Для перестановки 1 4 6 2 9 5 8 7
- 16. Рекурсивный метод поиска всех перестановок Метод рекурсивного перебора перестановок основан на идее сведения исходной задачи к
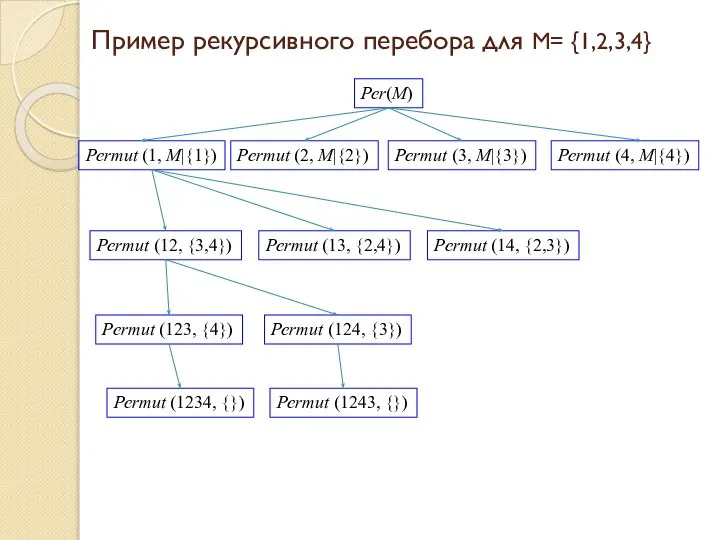
- 17. Пример рекурсивного перебора для M= {1,2,3,4} Реr(M) Реrmut (1, M|{1}) Реrmut (2, M|{2}) Реrmut (3, M|{3})
- 18. На языке Си этот процесс можно описать следующим образом: typedef char string[256]; void permut(string start, string
- 19. Генерация всех перестановок методом Кнута Идея: если построены все перестановки длины N, то для каждой такой
- 20. Генерация перестановок методом Кнута – 1 способ Пусть дана перестановка длины N. Дописать в конец перестановки
- 21. Генерация перестановок методом Кнута – 2 способ Пусть дана перестановка длины N: a1 a2 … aN
- 23. Скачать презентацию

















 Презентация на тему Параллелепипед
Презентация на тему Параллелепипед  Понятие многогранника
Понятие многогранника Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Слабое звено
Слабое звено Конкурс - викторина «Аас-кежиктиг таварылга»
Конкурс - викторина «Аас-кежиктиг таварылга» Организация обучения по математике. Принципы отбора содержания и составления дистанционного урока
Организация обучения по математике. Принципы отбора содержания и составления дистанционного урока Виды показательных уравнений и способы их решения
Виды показательных уравнений и способы их решения Великие о математике
Великие о математике «Концентр 1000, нумерация и сравнение чисел» В.Н.Рудницкая (Начальная школа XXI века)
«Концентр 1000, нумерация и сравнение чисел» В.Н.Рудницкая (Начальная школа XXI века) Устный счет в 3 классе. №3
Устный счет в 3 классе. №3 Табличное умножение (Соответствующие случаи деления)
Табличное умножение (Соответствующие случаи деления) Умножение чисел
Умножение чисел Поняття стійкості автоматичної системи. Математичні ознаки стійкості. Критерій Гурвіца
Поняття стійкості автоматичної системи. Математичні ознаки стійкості. Критерій Гурвіца Основы теории вероятностей. Случайные события
Основы теории вероятностей. Случайные события Функции и их графики. Интегрированный урок (алгебра + информатика)
Функции и их графики. Интегрированный урок (алгебра + информатика) Геометрический смысл производной
Геометрический смысл производной Логарифмы
Логарифмы Интерактивная игра. Задачи в стихах
Интерактивная игра. Задачи в стихах Устный счет по математике 5 класс Артамонова Л.В., учитель математики МКОУ «Москаленский лицей»
Устный счет по математике 5 класс Артамонова Л.В., учитель математики МКОУ «Москаленский лицей»  Координатно-параметрический метод решения задач с параметром
Координатно-параметрический метод решения задач с параметром Решение задания №3 ГИА
Решение задания №3 ГИА Основы теории погрешностей и математической статистики
Основы теории погрешностей и математической статистики Округление десятичных чисел
Округление десятичных чисел Математика в экономике. Реферат с элементами исследования по математике
Математика в экономике. Реферат с элементами исследования по математике Линейная функция и её график
Линейная функция и её график Statistical data processing
Statistical data processing Четырехугольники. Занимательные задачи
Четырехугольники. Занимательные задачи Презентация Действия с десятичными дробями
Презентация Действия с десятичными дробями