Содержание
- 2. Функции работы с изображениями Imshow Imwrite imread
- 3. Функции конвертации Im2bw Im2double Rgb2gray Uint8 uint16
- 4. Функции работы с матрицами Max Min Sum Zeros Ones .* и * ./ и /
- 5. Векторизация meshgrid
- 6. Общие задания
- 7. Вывод сферического волновоо фронта Задача: вывести на экран картинку сферического (кругового в 2D случае) волнового фронта
- 8. Перестановки Задача: реализовать функцию, принимающую на вход произвольный набор элементов, результатом работы которой является список всех
- 9. Дискретное преобразование Фурье Дискретное преобразование Фурье N – число элементов последовательности (размер массива) k – k-ый
- 10. Дискретное преобразование Фурье Обратное дискретное преобразование Фурье Поворачивающий множитель
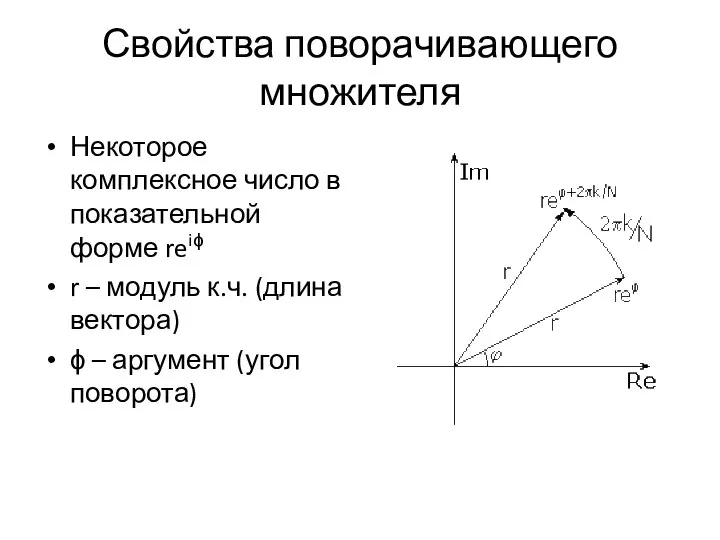
- 11. Свойства поворачивающего множителя k – степень, а не индекс. Если равен 1, то не записываем ДПФ
- 12. Свойства поворачивающего множителя Некоторое комплексное число в показательной форме reiϕ r – модуль к.ч. (длина вектора)
- 13. Свойства поворачивающего множителя wkN , модуль равен 1, а фаза – 2π/N При умножении к.ч. В
- 14. Теорема 0 Теорема: Если комплексное число представлено в виде e j2πN, где N - целое, то
- 15. Теорема 1 Теорема: Величина периодична по k и по n с периодом N. То есть, для
- 16. Теорема 1 Доказательство: Величина -h = -(nl+mk+mlN) - целая, так как все множители целые, и все
- 17. Теорема 2 Теорема: Для величины справедлива формула: Доказательство:
- 18. Быстрое преобразование Фурье Идея: Необходимо разделить сумму в формуле ДПФ из N слагаемых на две суммы
- 19. Быстрое преобразование Фурье Применяют: «Прореживание по времени», когда в первую сумму попадают слагаемые с четными номерами,
- 20. Теорема 3 Определим еще две последовательности: {x[even]} и {x[odd]} через последовательность {x} следующим образом: x[even]n =x2n,
- 22. Скачать презентацию

















![Теорема 3 Определим еще две последовательности: {x[even]} и {x[odd]} через последовательность](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1469622/slide-19.jpg)
 Социально-экономическая статистика
Социально-экономическая статистика Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Лекция 1. Исследование функции
Лекция 1. Исследование функции Порядок выполнения действий 5 класс
Порядок выполнения действий 5 класс  Презентация по математике "Ферма Пьер" - скачать
Презентация по математике "Ферма Пьер" - скачать  Случайные величины
Случайные величины Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников Оценивание образовательных результатов обучающихся основной школы при освоении предметной области «Математика»
Оценивание образовательных результатов обучающихся основной школы при освоении предметной области «Математика»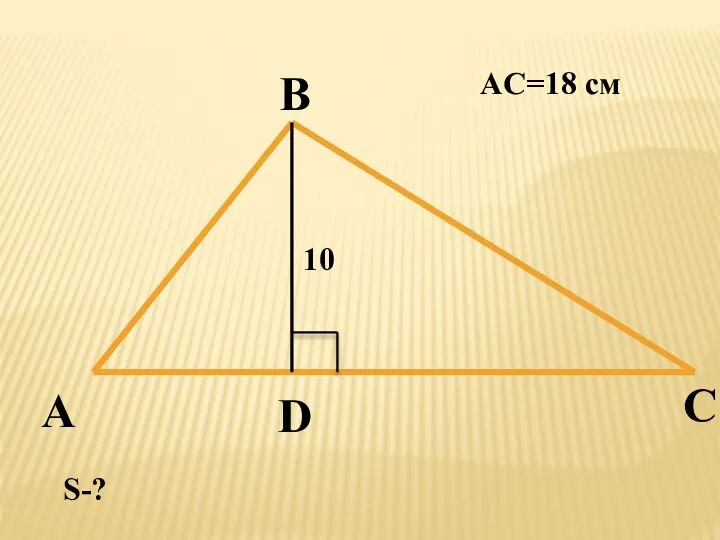 Площадь треугольника
Площадь треугольника Цилиндр
Цилиндр Симметрия в архитектуре
Симметрия в архитектуре 0пределение расстояния до недоступной точки
0пределение расстояния до недоступной точки Уравнение вида x² = a
Уравнение вида x² = a ДЕМО вариант 2016
ДЕМО вариант 2016 План воспитательной работы
План воспитательной работы Формулы приведения
Формулы приведения Прямоугольные треугольники и некоторые их свойства
Прямоугольные треугольники и некоторые их свойства Вычисление площади многоугольника
Вычисление площади многоугольника Линейные ДУ n-го порядка
Линейные ДУ n-го порядка Урок по алгебре в 11 классе Выполнила учительница математики МОУ «Аминевская СОШ» Юсупова Эльфия Лутфулловна 2006 год
Урок по алгебре в 11 классе Выполнила учительница математики МОУ «Аминевская СОШ» Юсупова Эльфия Лутфулловна 2006 год Презентация по математике "Решение неравенств методом интервалов" - скачать бесплатно
Презентация по математике "Решение неравенств методом интервалов" - скачать бесплатно Состав числа 10
Состав числа 10 Задачи: условие, требование, решение
Задачи: условие, требование, решение Параллельный перенос вдоль оси координат
Параллельный перенос вдоль оси координат Оценка достоверности относительных и средних величин
Оценка достоверности относительных и средних величин Теория вероятностей. Определение вероятности случайного события. Элементы комбинаторики
Теория вероятностей. Определение вероятности случайного события. Элементы комбинаторики Разминка. Линейная функция
Разминка. Линейная функция Детективное агентство «…» «Натуральные числа».
Детективное агентство «…» «Натуральные числа».