Содержание
- 2. Поверхность, одно из основных геометрических понятий Поверхности составляют широкое многообразие нелинейных фигур трехмерного пространства. Инженерная деятельность
- 3. Рассматривая поверхности как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида
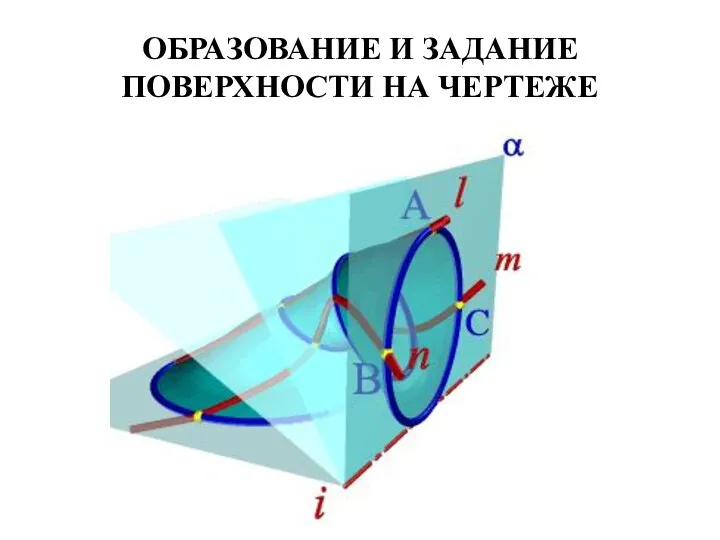
- 4. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТИ НА ЧЕРТЕЖЕ Поверхность можно рассматривать, как совокупность последовательных положений линии l, перемещающейся
- 5. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТИ НА ЧЕРТЕЖЕ Подвижную линию принято называть образующей, неподвижные – направляющими. Такой способ
- 6. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТИ НА ЧЕРТЕЖЕ
- 7. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТИ НА ЧЕРТЕЖЕ По виду образующей различают поверхности линейчатые и нелинейчатые. образующая линейчатых
- 8. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТИ НА ЧЕРТЕЖЕ Линейчатые поверхности в свою очередь разделяют на так называемые развертывающие,
- 9. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТИ НА ЧЕРТЕЖЕ Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса.
- 10. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТИ НА ЧЕРТЕЖЕ Циклические поверхности подразделяются на: ·Поверхности вращения; ·Винтовые поверхности; ·Поверхности с
- 11. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТИ НА ЧЕРТЕЖЕ
- 12. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТИ НА ЧЕРТЕЖЕ Множество линий, заполняющих поверхность так, что через каждую точку поверхности
- 13. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТИ НА ЧЕРТЕЖЕ Проекции каркаса могут быть построены, если задан определитель поверхности –
- 14. Определитель: Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые
- 15. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТИ НА ЧЕРТЕЖЕ
- 16. Определитель: Геометрическая часть определителя: три направляющих l, m, n, ось i пучка плоскостей Алгоритмическая часть: выделяем
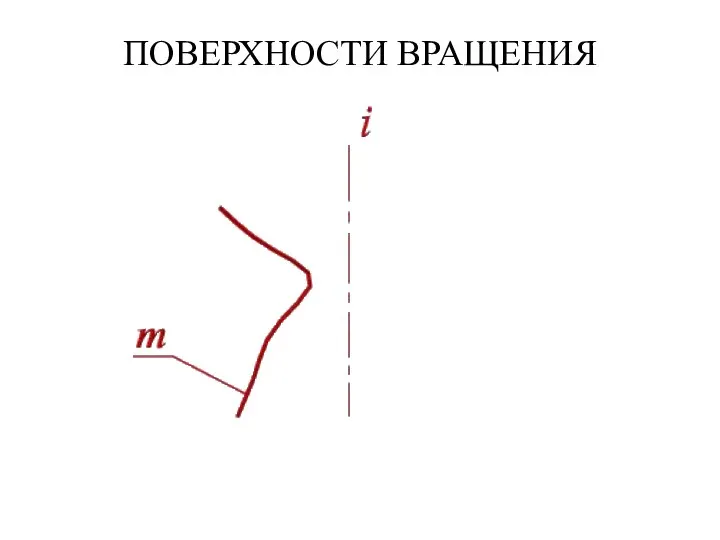
- 17. ПОВЕРХНОСТИ ВРАЩЕНИЯ Поверхности вращения – это поверхности созданные при вращении образующей m вокруг оси i .
- 18. ПОВЕРХНОСТИ ВРАЩЕНИЯ Геометрическая часть определителя состоит из двух линий: образующей m и оси i. Алгоритмическая часть
- 19. ПОВЕРХНОСТИ ВРАЩЕНИЯ
- 20. ПОВЕРХНОСТИ ВРАЩЕНИЯ
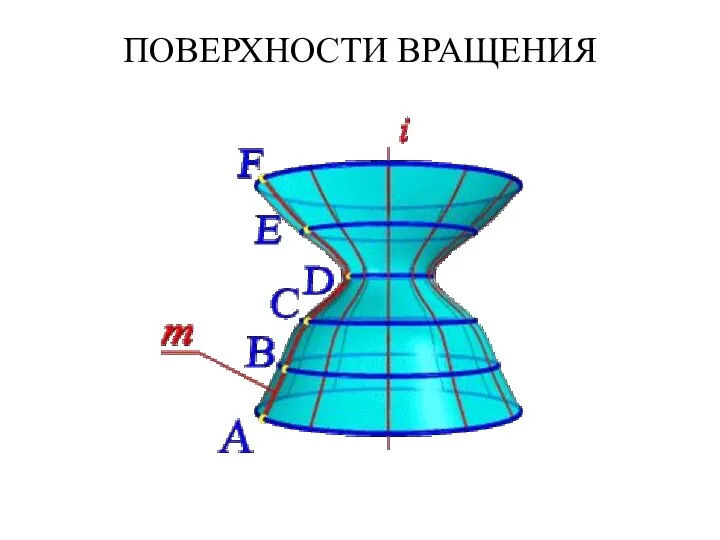
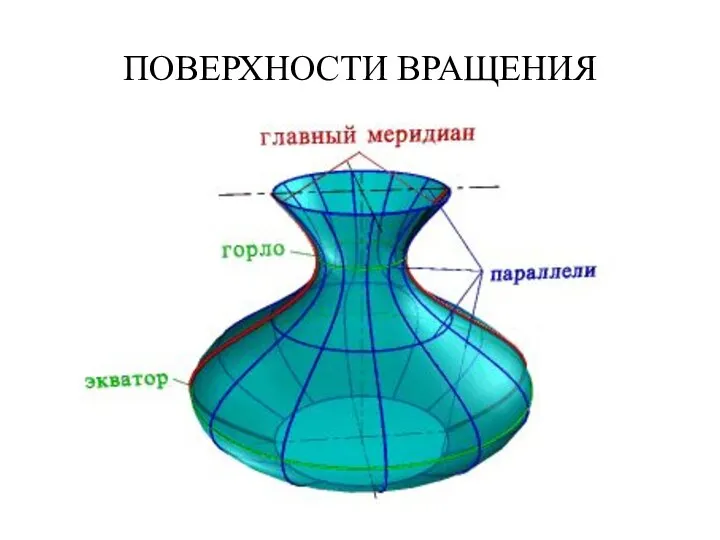
- 21. ПОВЕРХНОСТИ ВРАЩЕНИЯ Так создается каркас поверхности, состоящей из множества окружностей, плоскости которых расположены перпендикулярно оси i.
- 22. ПОВЕРХНОСТИ ВРАЩЕНИЯ Из закона образования поверхности вращения вытекают два основных свойства: 1. Плоскость перпендикулярная оси вращения,
- 23. ПОВЕРХНОСТИ ВРАЩЕНИЯ
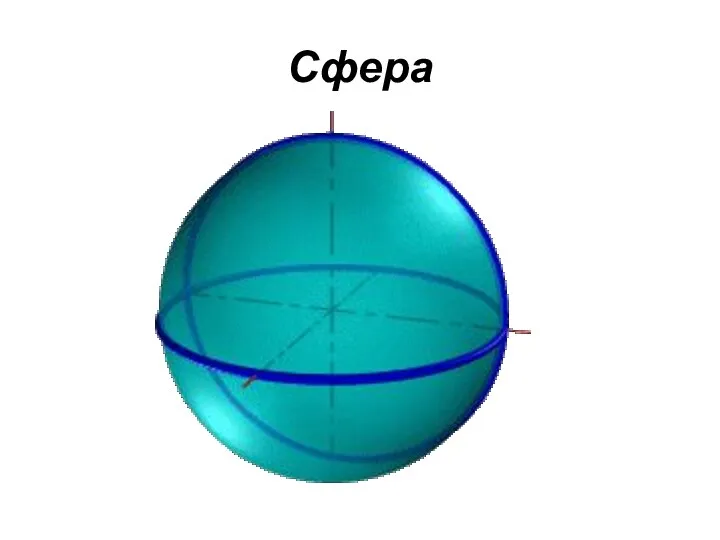
- 24. ПОВЕРХНОСТИ ВРАЩЕНИЯ Рассмотрим наиболее распространенные поверхности вращения с криволинейными образующими: Сфера – образуется вращением окружности вокруг
- 25. Сфера
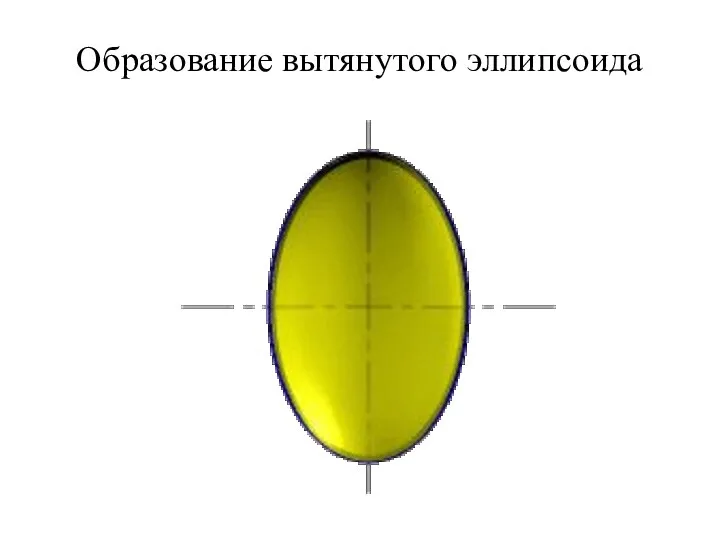
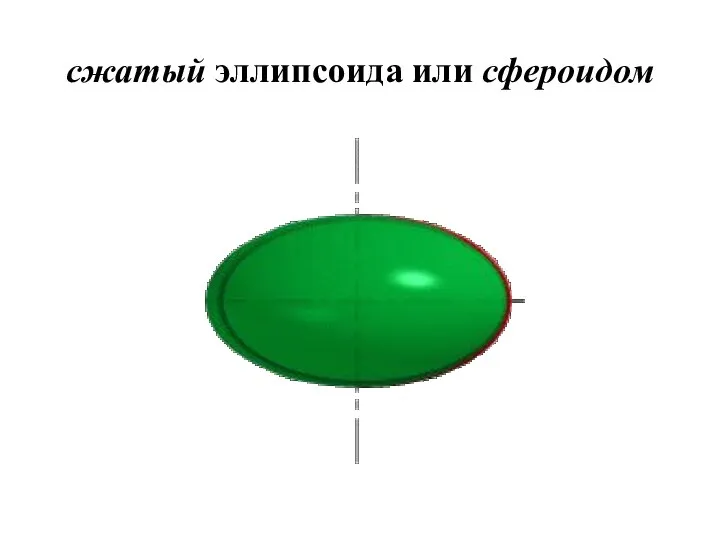
- 26. Эллипсоиды При сжатии или растяжении сферы она преобразуется в эллипсоиды, которые могут быть получены вращением эллипса
- 27. Образование вытянутого эллипсоида
- 28. сжатый эллипсоида или сфероидом
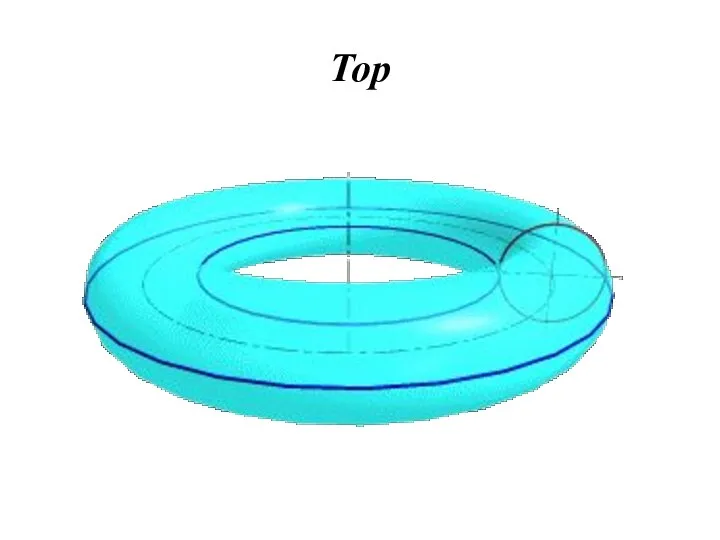
- 30. ПОВЕРХНОСТИ ВРАЩЕНИЯ Тор – поверхность тора формируется при вращении окружности вокруг оси, не проходящей через центр
- 31. Тор
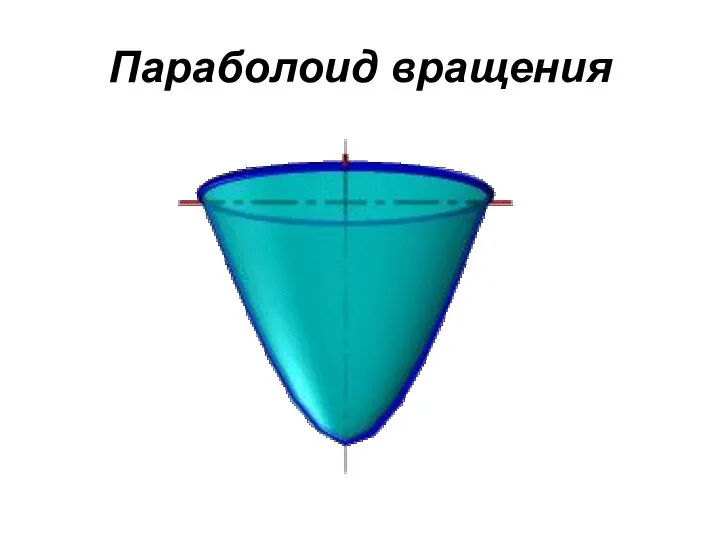
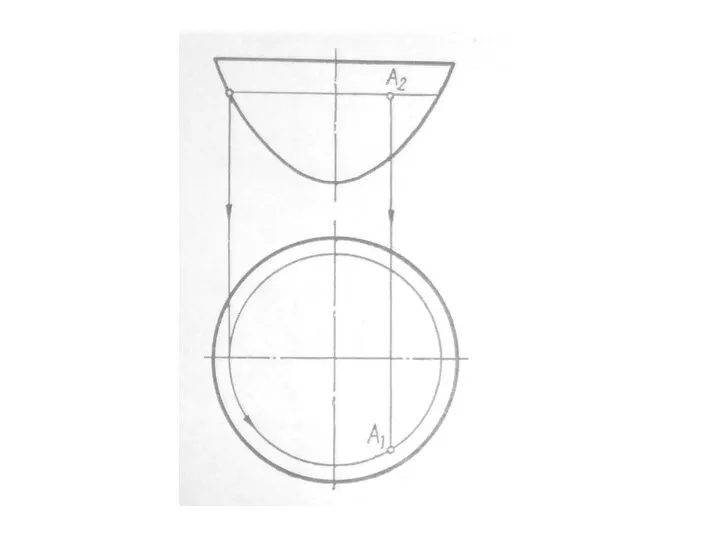
- 32. ПОВЕРХНОСТИ ВРАЩЕНИЯ Параболоид вращения – образуется при вращении параболы вокруг своей оси
- 33. Параболоид вращения
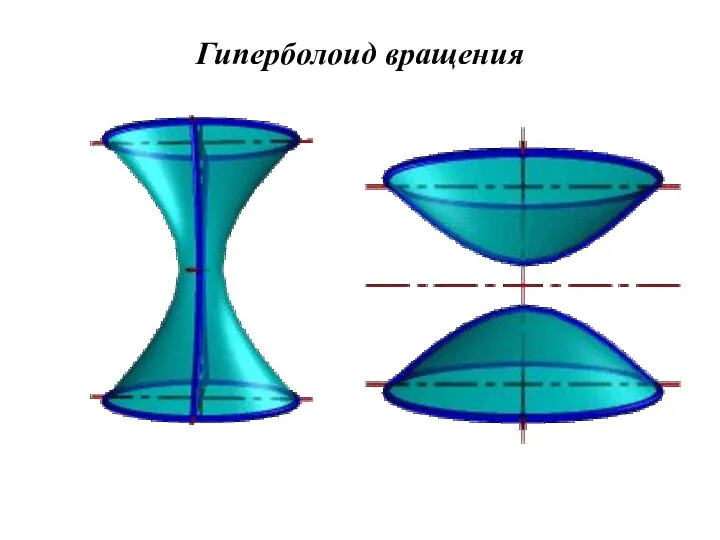
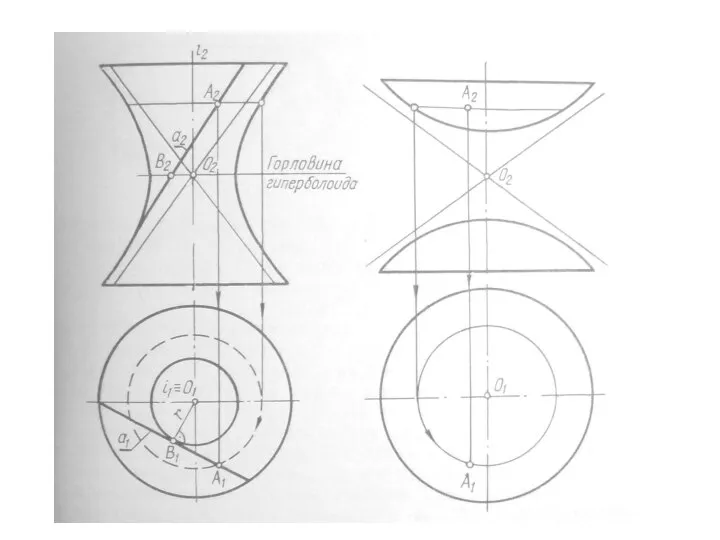
- 35. Гиперболоид вращения различают одно и двух полостной гиперболоиды вращения. Первый получается при вращении вокруг мнимой оси,
- 36. Гиперболоид вращения
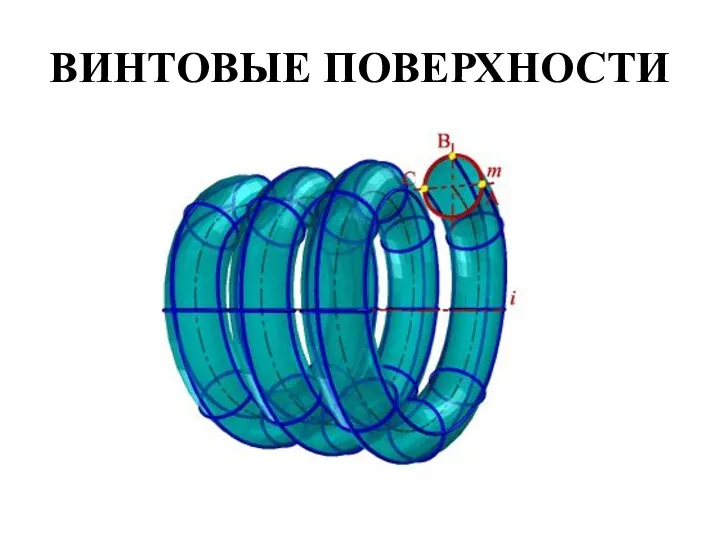
- 38. ВИНТОВЫЕ ПОВЕРХНОСТИ Винтовые поверхности образуются винтовым движением некоторой линии – образующей. Под винтовым движением понимается совокупность
- 39. ВИНТОВЫЕ ПОВЕРХНОСТИ
- 40. ВИНТОВЫЕ ПОВЕРХНОСТИ Геометрическая часть определителя винтовой поверхности ни чем не отличается от поверхности вращения и состоит
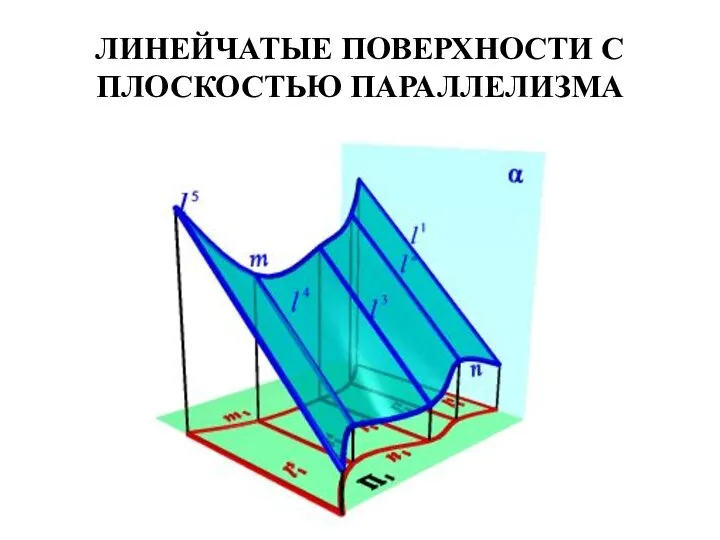
- 41. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ ПАРАЛЛЕЛИЗМА Поверхность с плоскостью параллелизма представляет собой множество прямых линий l (образующих),
- 42. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ ПАРАЛЛЕЛИЗМА
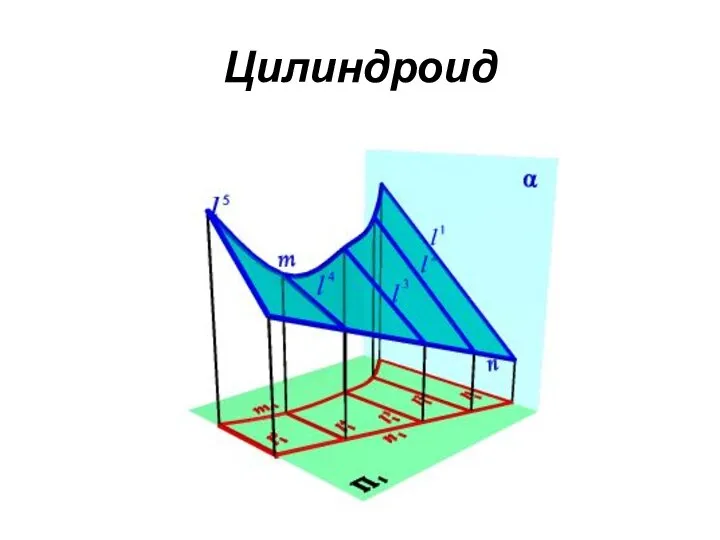
- 43. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ ПАРАЛЛЕЛИЗМА В зависимости от формы направляющих образуются три частных вида поверхностей. Цилиндроид.
- 44. Цилиндроид
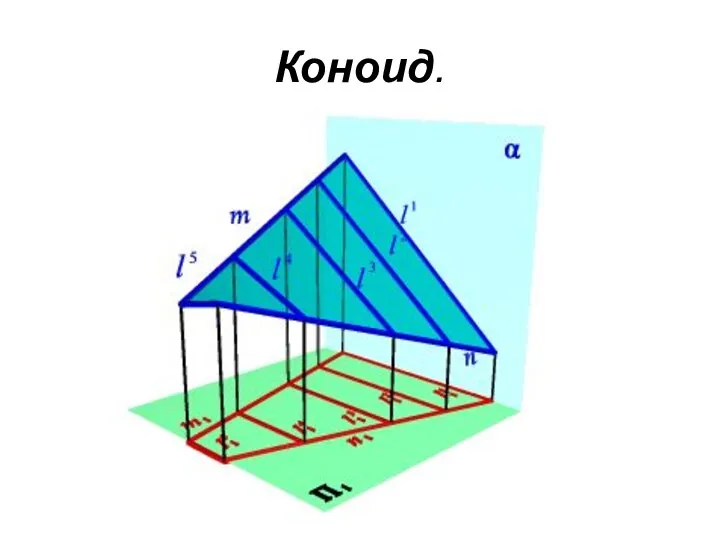
- 45. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ ПАРАЛЛЕЛИЗМА Коноид. Коноидом называется поверхность, образованная движением прямолинейной образующей по двум направляющим,
- 46. Коноид.
- 47. ПОВЕРХНОСТИ ПАРАЛЛЕЛЬНОГО ПЕРЕНОСА Поверхностью параллельного переноса называется поверхность, образованная поступательным плоскопараллельным перемещением образующей - плоской кривой
- 48. ПОВЕРХНОСТИ ПАРАЛЛЕЛЬНОГО ПЕРЕНОСА Геометрическая часть определителя состоит из двух кривых линий образующей - m и направляющей
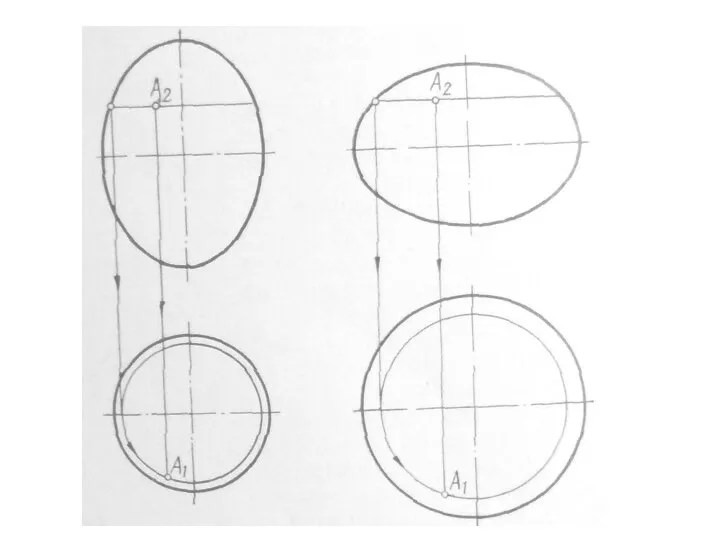
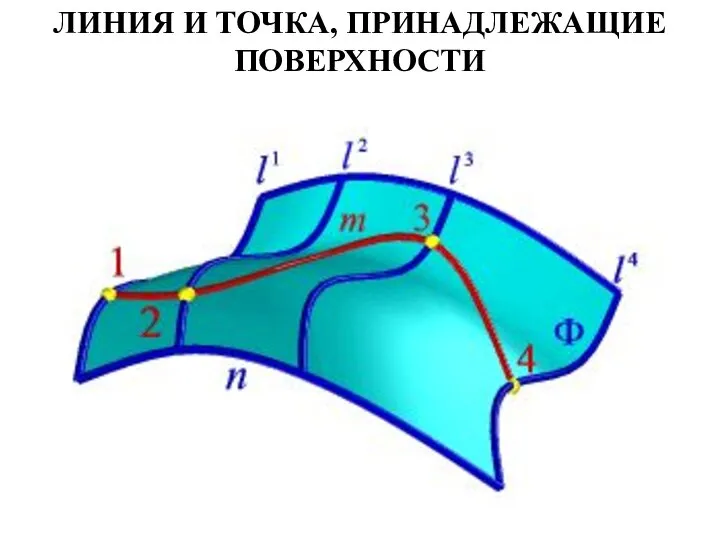
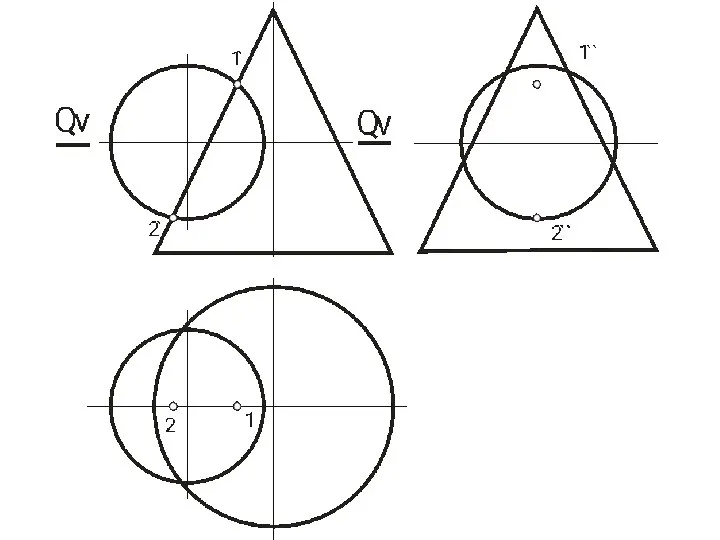
- 49. ЛИНИЯ И ТОЧКА, ПРИНАДЛЕЖАЩИЕ ПОВЕРХНОСТИ Для определения принадлежности точки и линии поверхности рассмотрим следующие позиционные задачи:
- 50. ЛИНИЯ И ТОЧКА, ПРИНАДЛЕЖАЩИЕ ПОВЕРХНОСТИ
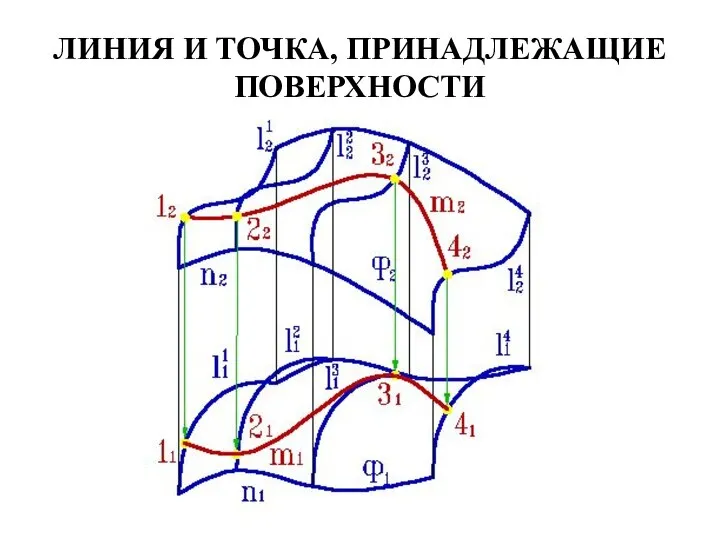
- 51. ЛИНИЯ И ТОЧКА, ПРИНАДЛЕЖАЩИЕ ПОВЕРХНОСТИ
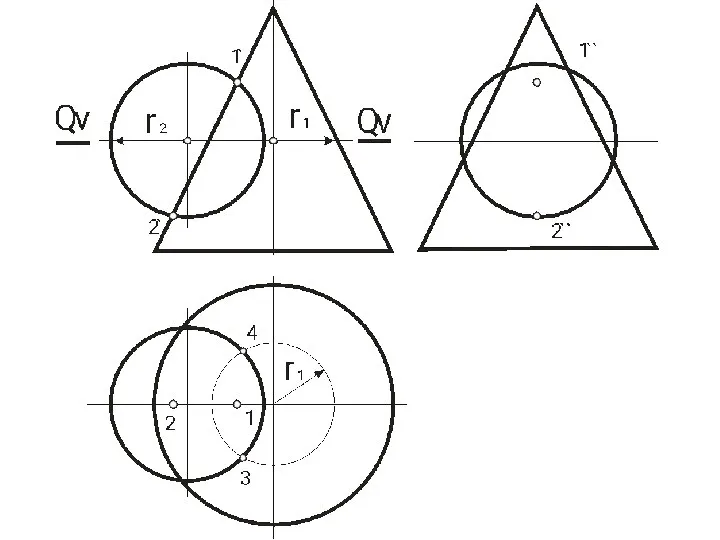
- 52. ЛИНИЯ И ТОЧКА, ПРИНАДЛЕЖАЩИЕ ПОВЕРХНОСТИ Алгоритм решения задачи: 1. Находим точки 12, 22, 32, 42 пересечения
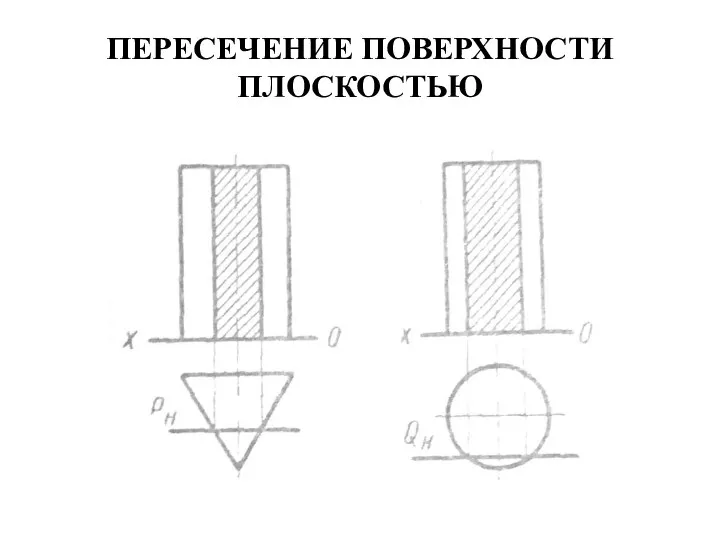
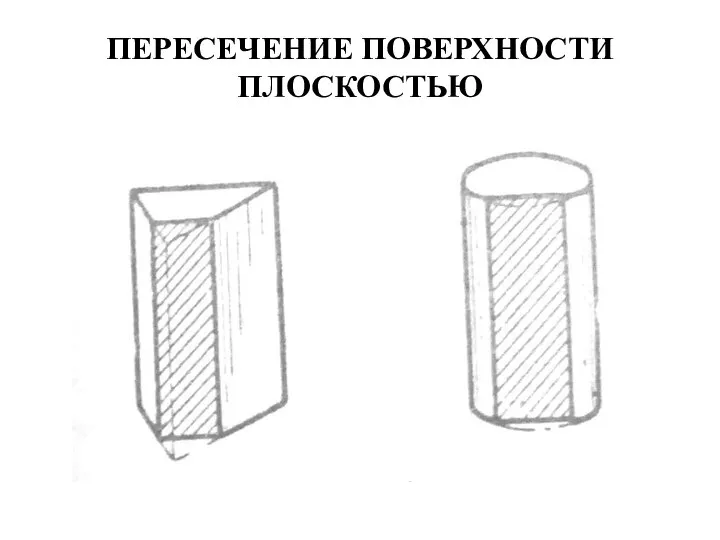
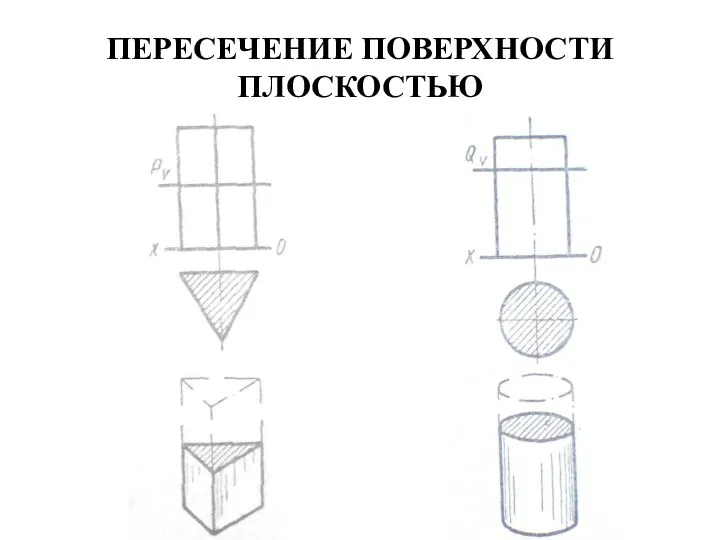
- 53. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ Пересечение плоскостью тел с параллельными образующими (призмы и цилиндры). Простейшие сечения получают плоскостями,
- 54. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ
- 55. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ
- 56. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ
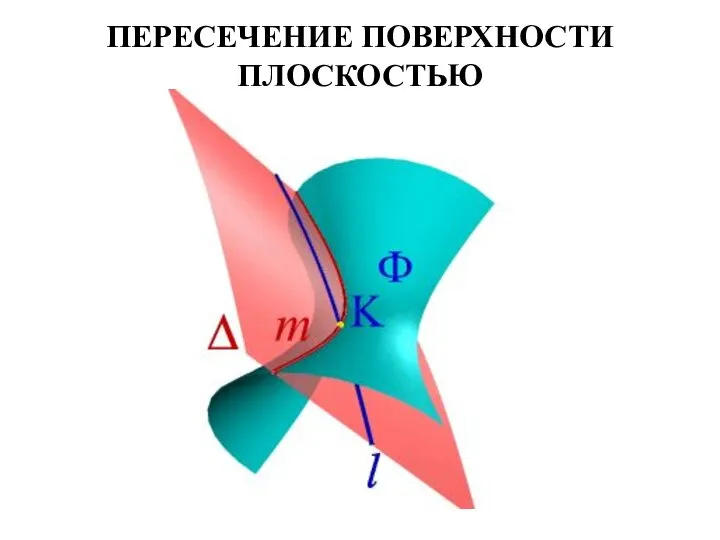
- 57. Построение линий пересечения поверхностей В общем случае линия пересечения двух кривых поверхностей представляет из себя пространственную
- 58. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ Наиболее простым является случай, когда плоскость проецирующая. Рассмотрим решение задачи по определению линии
- 59. МЕТОД ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ ПЛОСКОСТЕЙ Вспомогательные секущие плоскости чаще всего выбирают проецирующими и параллельными одной из плоскостей
- 60. МЕТОД ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ ПЛОСКОСТЕЙ Этот способ рекомендуется применять, если сечения заданных поверхностей одной и той же
- 61. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ
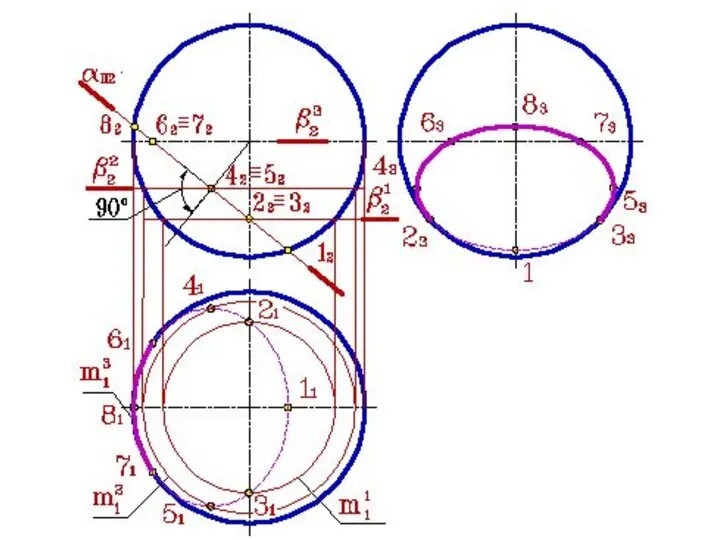
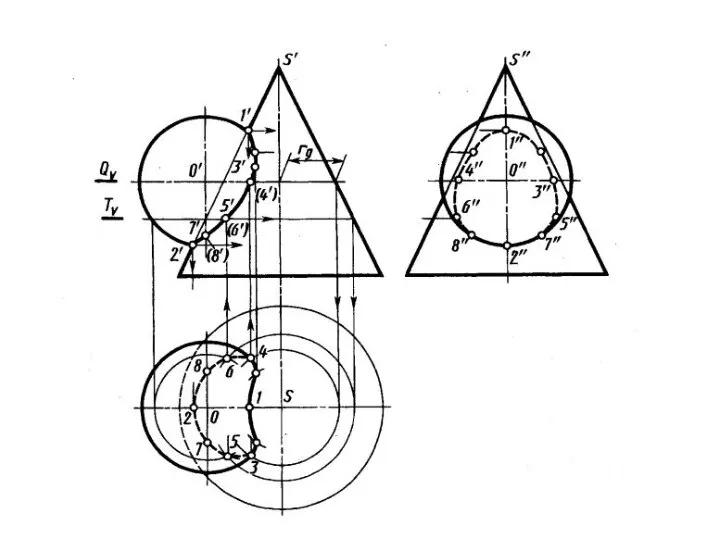
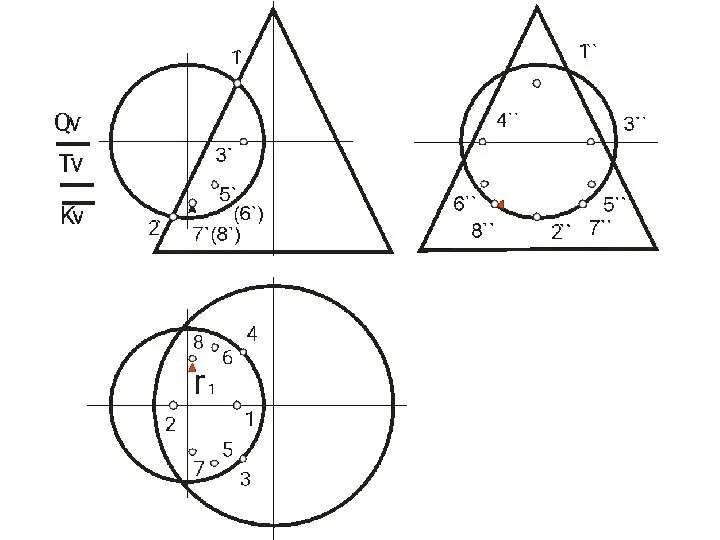
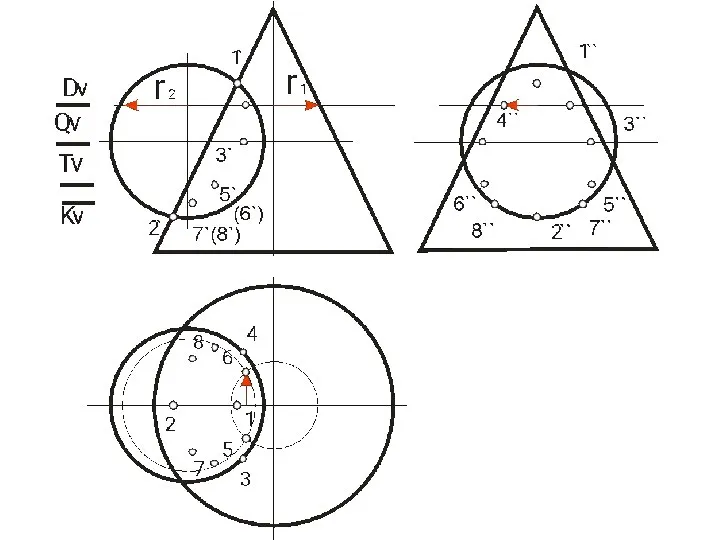
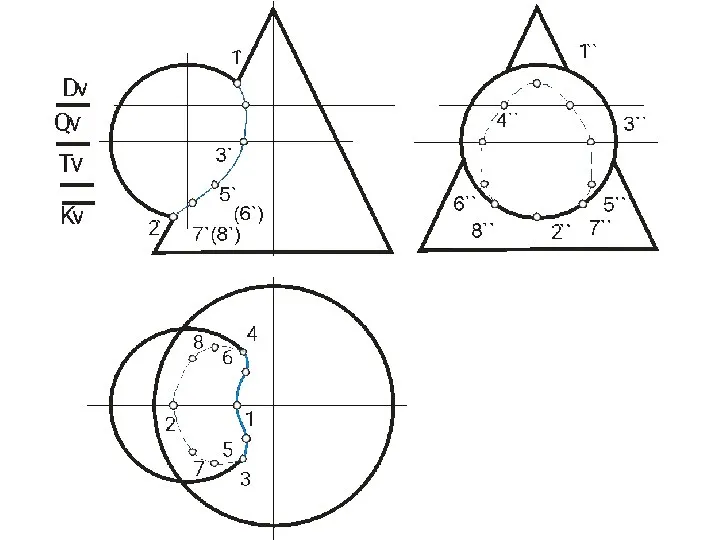
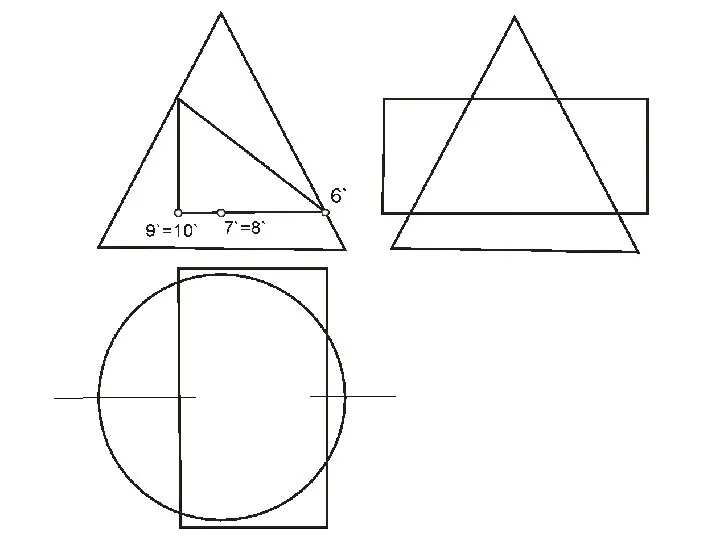
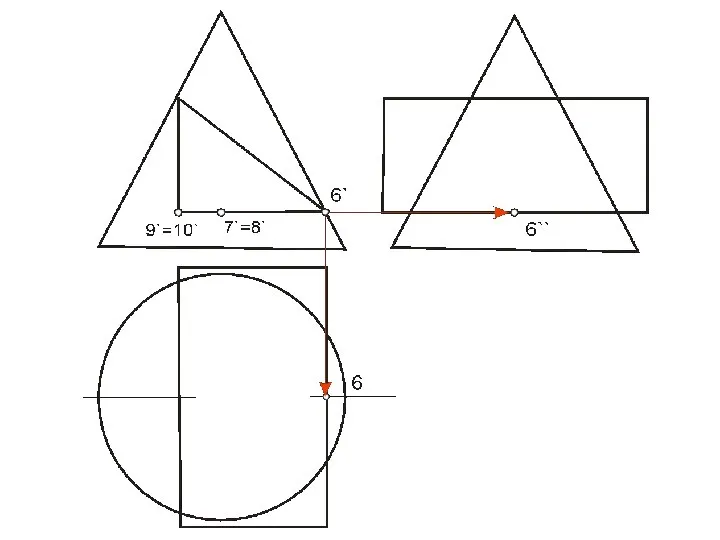
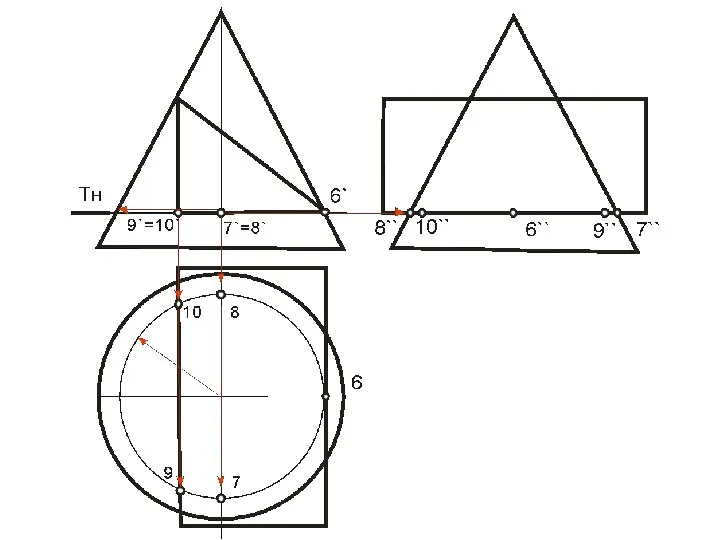
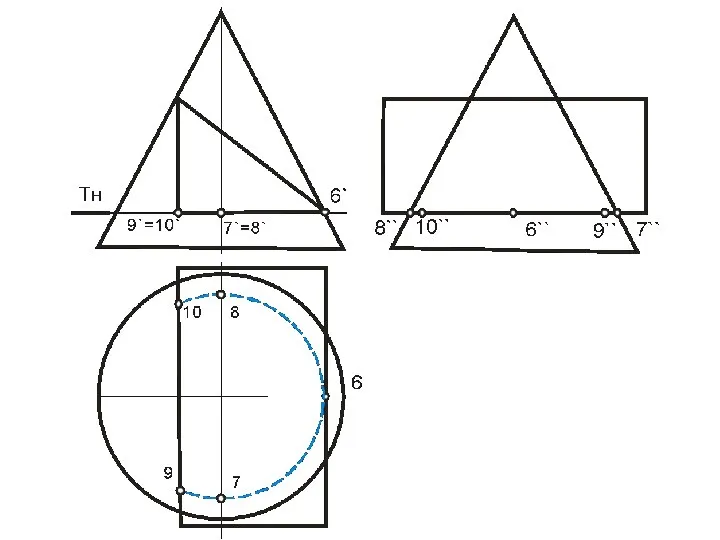
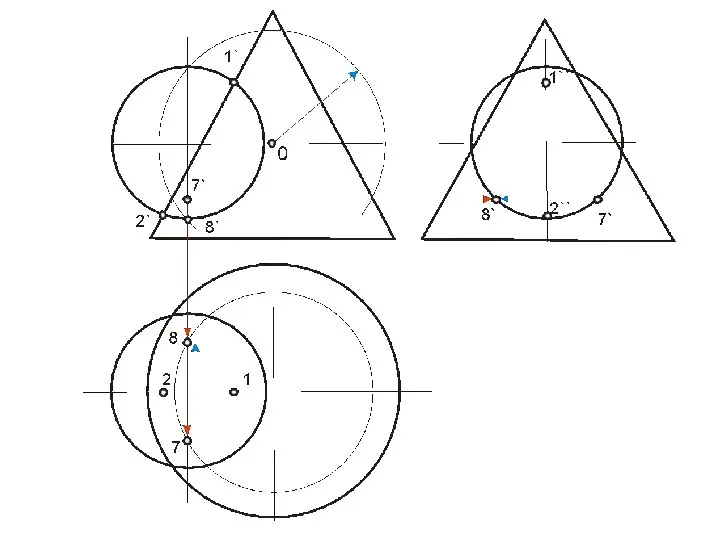
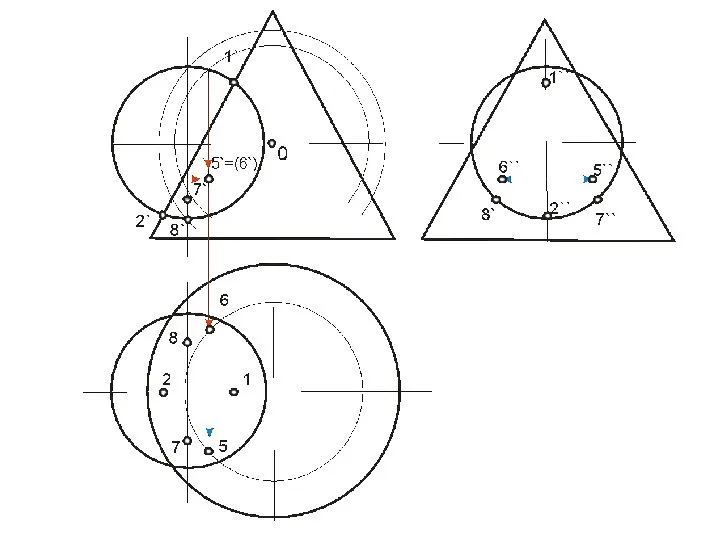
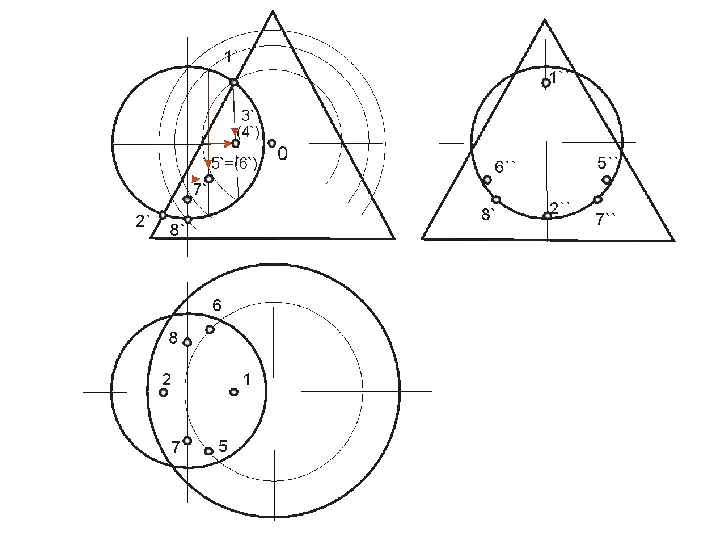
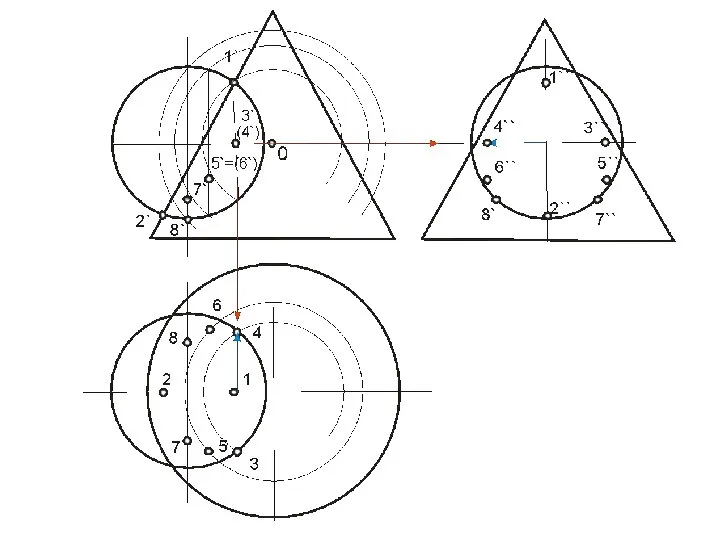
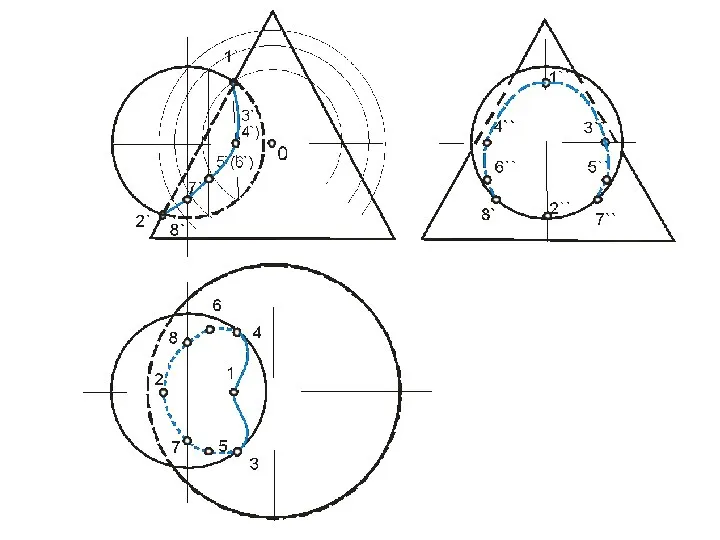
- 62. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ Окружность, по которой плоскость α пересекает сферу, проецируется на плоскости горизонтальную и профильную
- 64. Охарактеризуем выбранные для построения точки: ·1, 8- две вершины эллипса, определяющие положение малой оси, их фронтальные
- 65. Линия пересечения плоскости α и сферы на фронтальной плоскости проекций совпадает со следом плоскости на ней
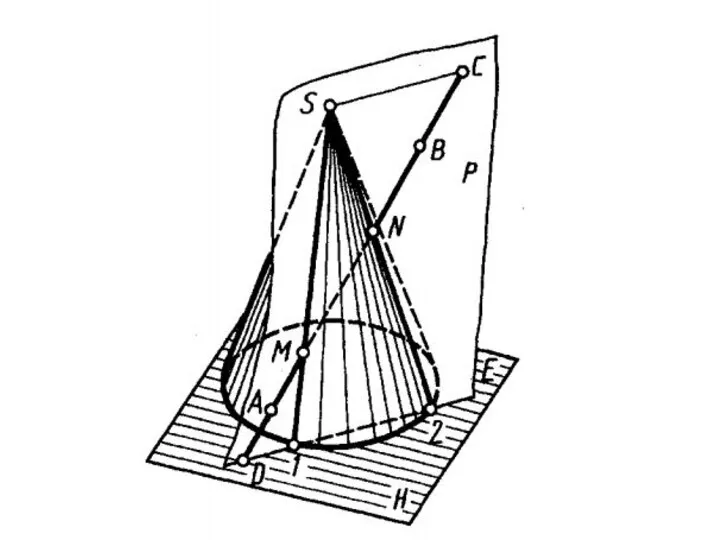
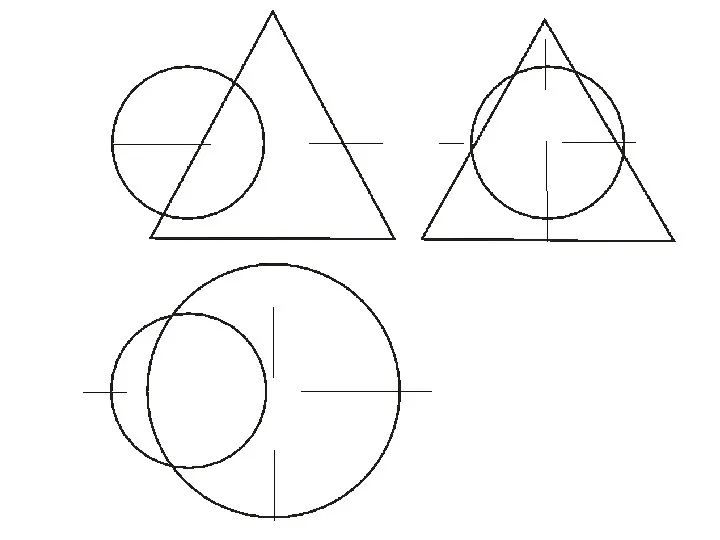
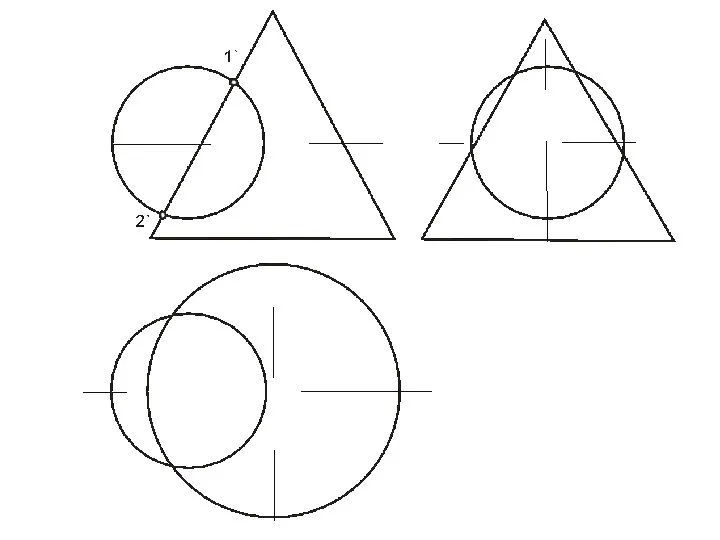
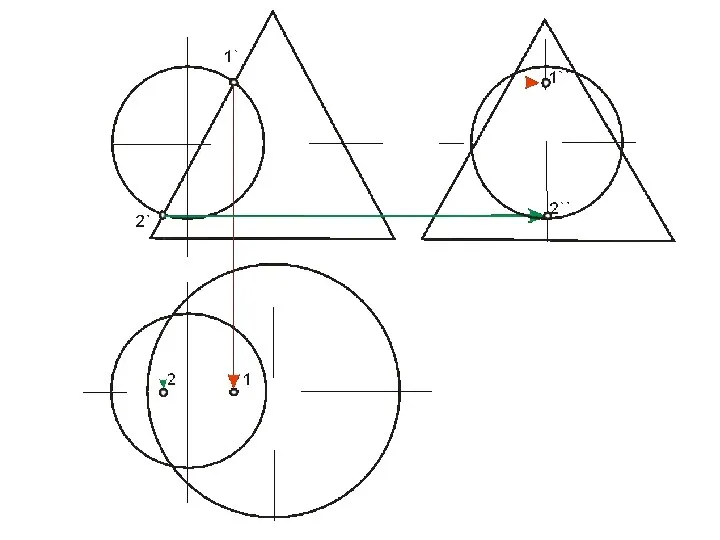
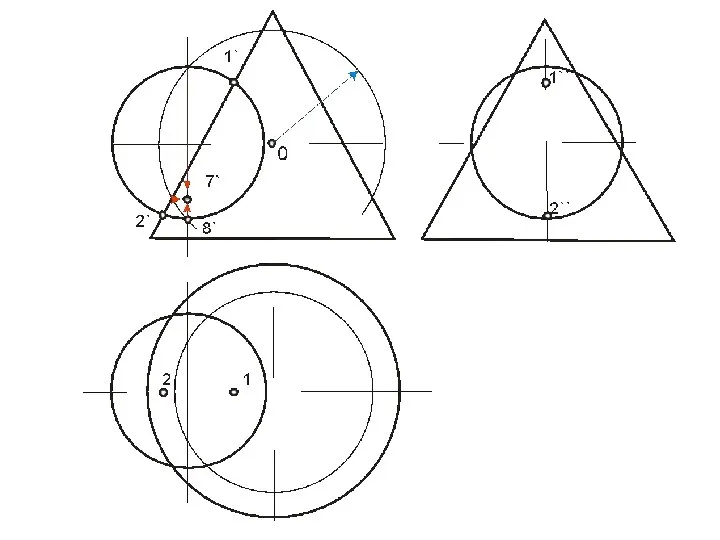
- 66. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ В общем случае для графического определения точек пересечения линии с поверхностью необходимо выполнить
- 67. ПЕРЕСЕЧЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ ПРЯМОЙ С ПОВЕРХНОСТЬЮ ПЛОСКОСТИ 1. Заключаем прямую линию в некоторую дополнительную плоскость (в
- 68. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ
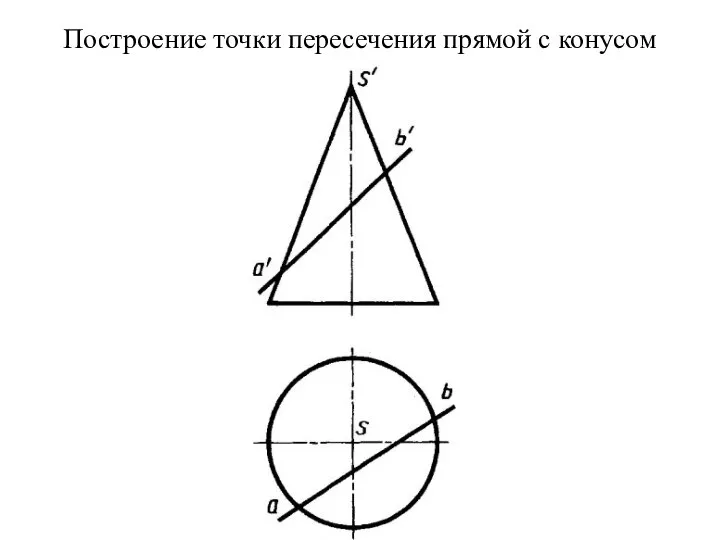
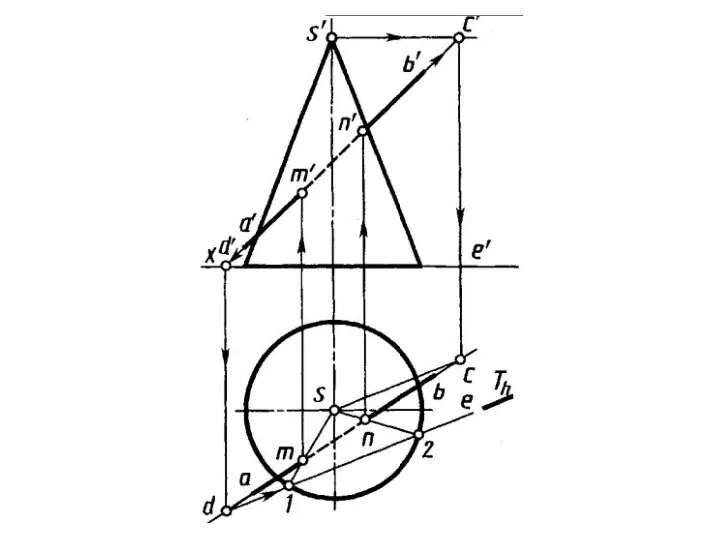
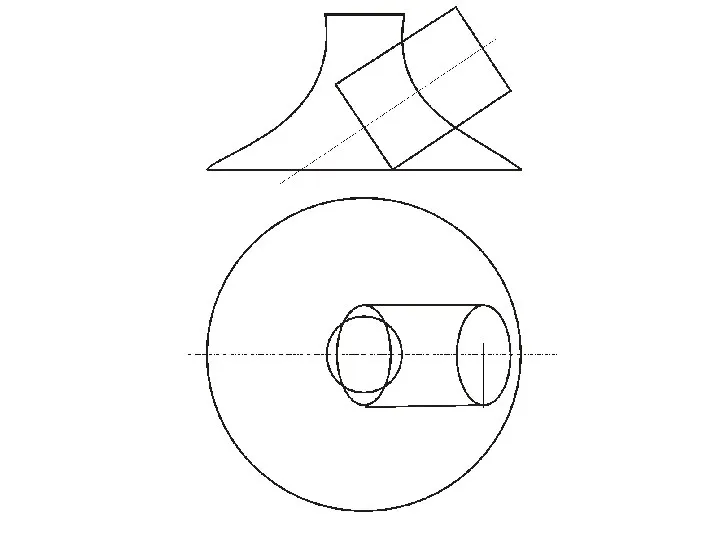
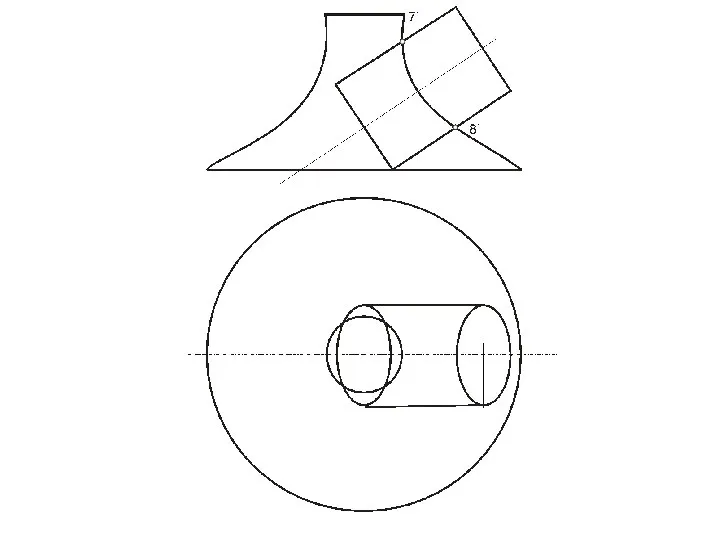
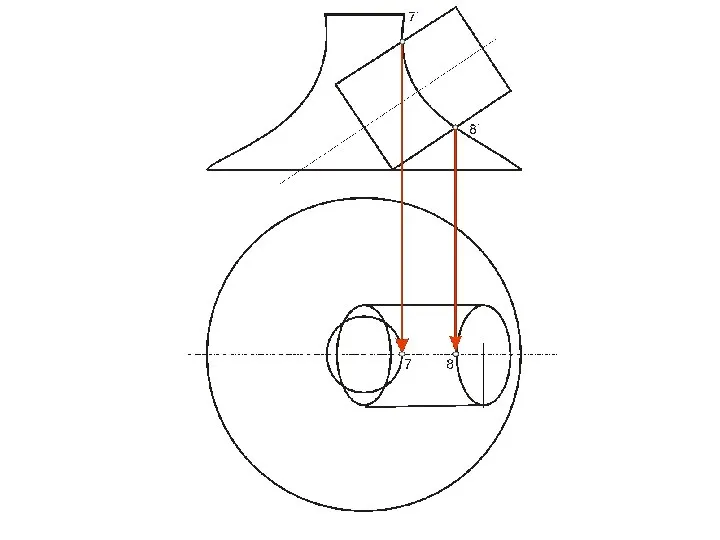
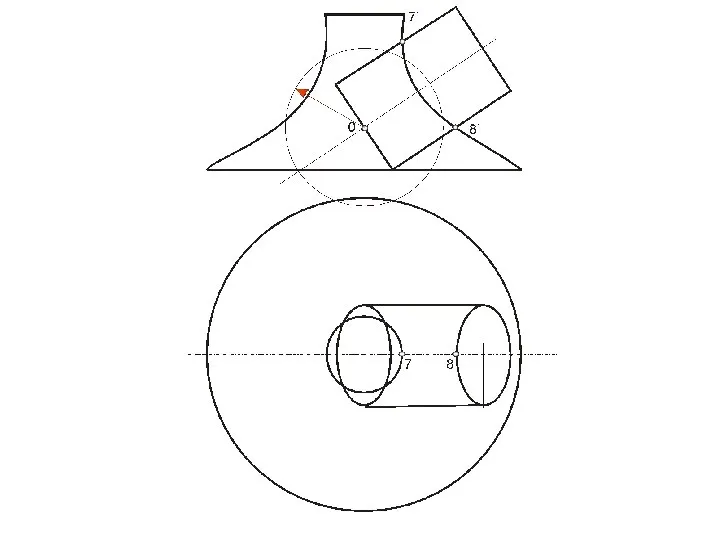
- 69. Построение точки пересечения прямой с конусом
- 72. Конические сечения В зависимости от положения секущей плоскости линиями сечения конической поверхности могут быть : эллипс,
- 73. Если плоскость пересекает все образующие поверхности конуса вращения, то линией сечения является эллипс. В этом случае
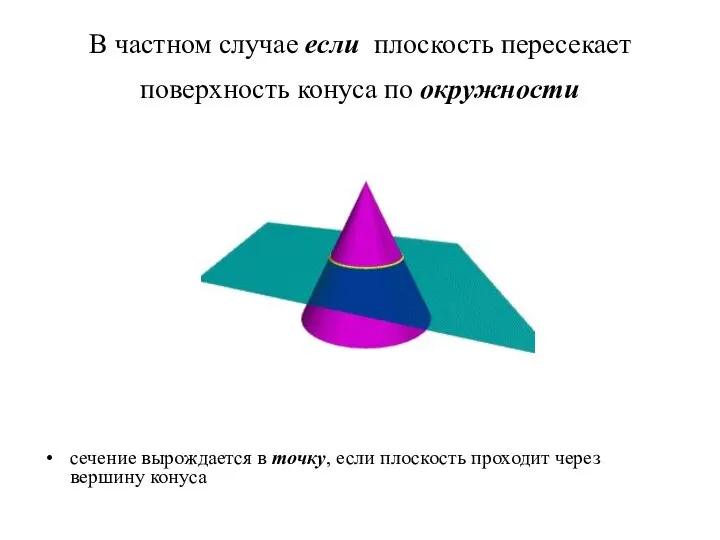
- 74. В частном случае если плоскость пересекает поверхность конуса по окружности сечение вырождается в точку, если плоскость
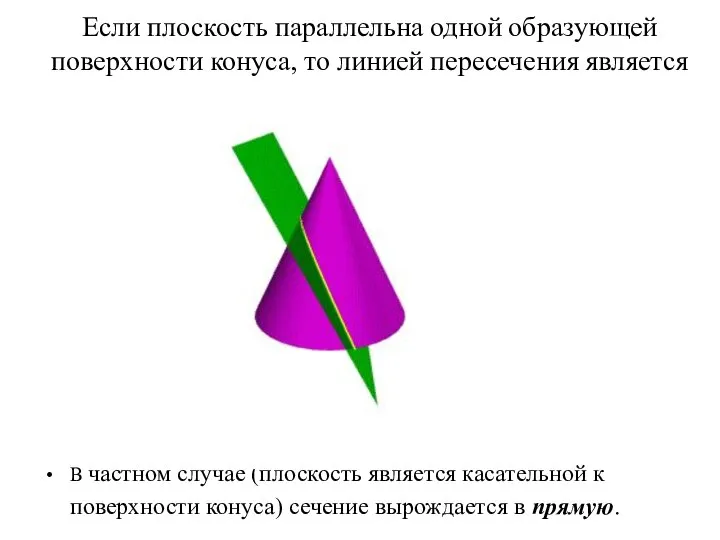
- 75. Если плоскость параллельна одной образующей поверхности конуса, то линией пересечения является парабола В частном случае (плоскость
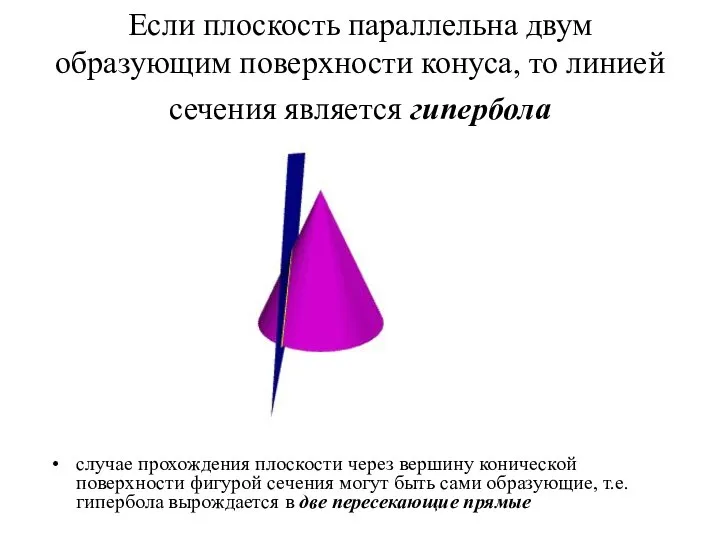
- 76. Если плоскость параллельна двум образующим поверхности конуса, то линией сечения является гипербола случае прохождения плоскости через
- 77. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ Линией пересечения двух поверхностей является множество точек, общих для данных поверхностей. 1. Из
- 78. Секущие поверхности-посредники выбираются так, чтобы они, пересекаясь с данными поверхностями, давали простые для построения линии, например
- 79. Метод секущих плоскостей Вспомогательные секущие плоскости чаще всего выбирают проецирующими и параллельными одной из плоскостей проекций
- 80. Алгоритм 1) Определяем опорные точки линии пересечения 2) Находим их горизонтальные проекции 3) Рассекаем обе поверхности
- 83. Определяем опорные точки линии пересечения
- 85. Находим их горизонтальные и профильные проекции
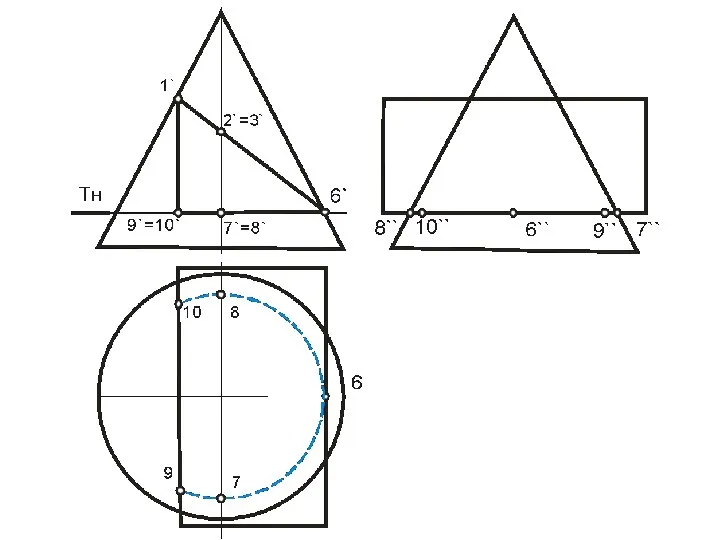
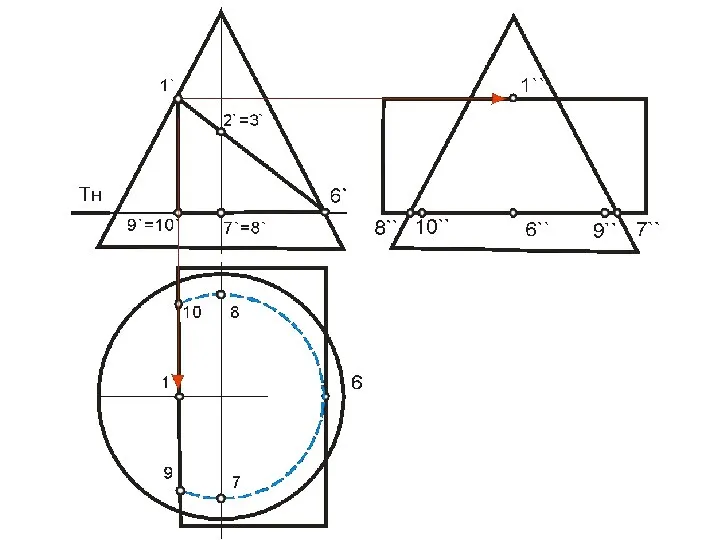
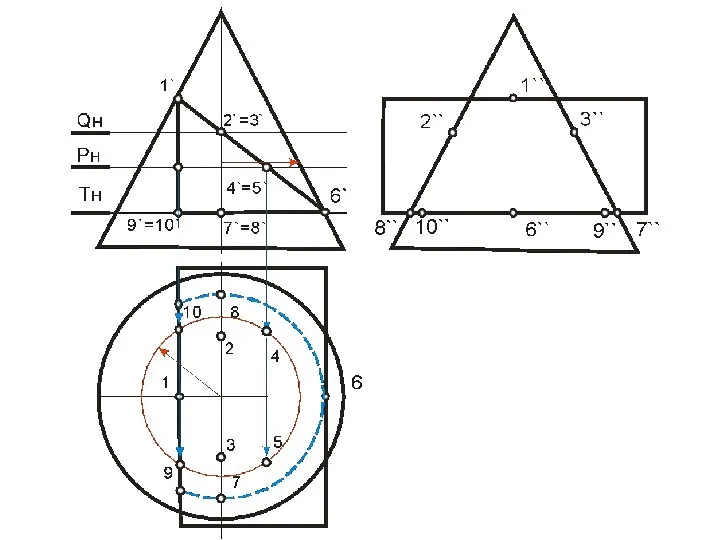
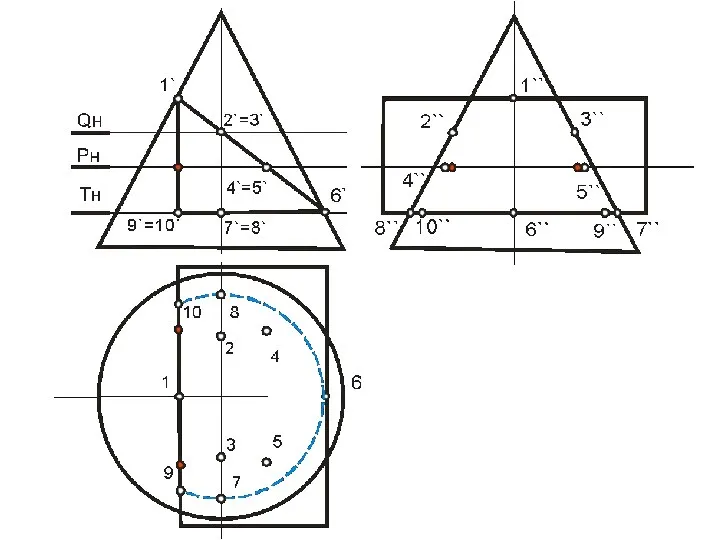
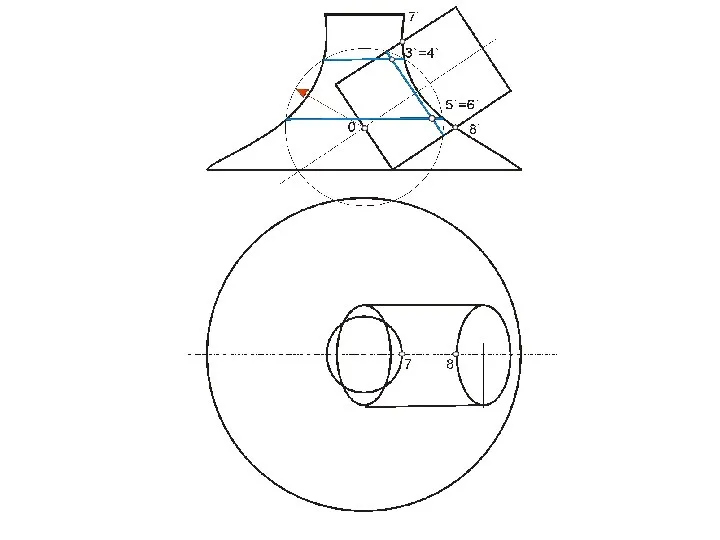
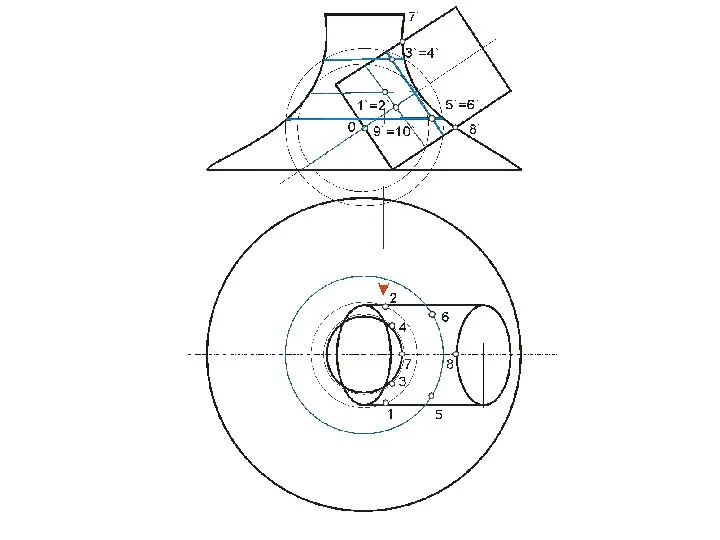
- 96. Построение линии пересечения треугольной призмы с конусом
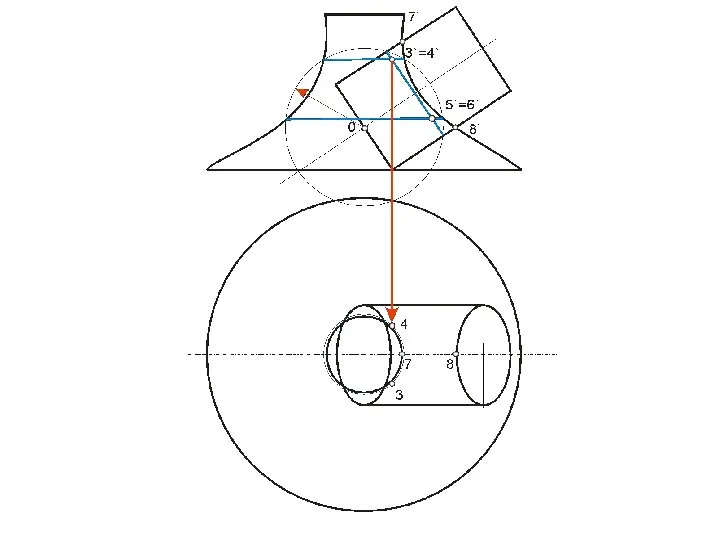
- 97. Алгоритм 1) Определяем опорные точки линии пересечения 2) Находим их горизонтальные проекции 3) Рассекаем обе поверхности
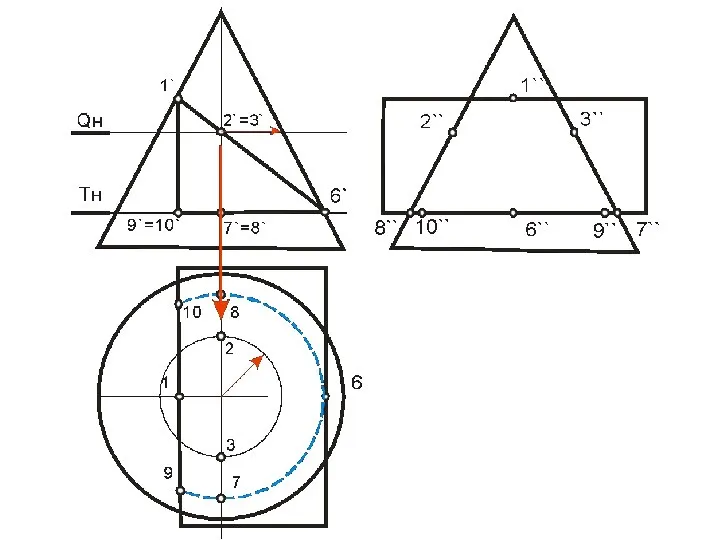
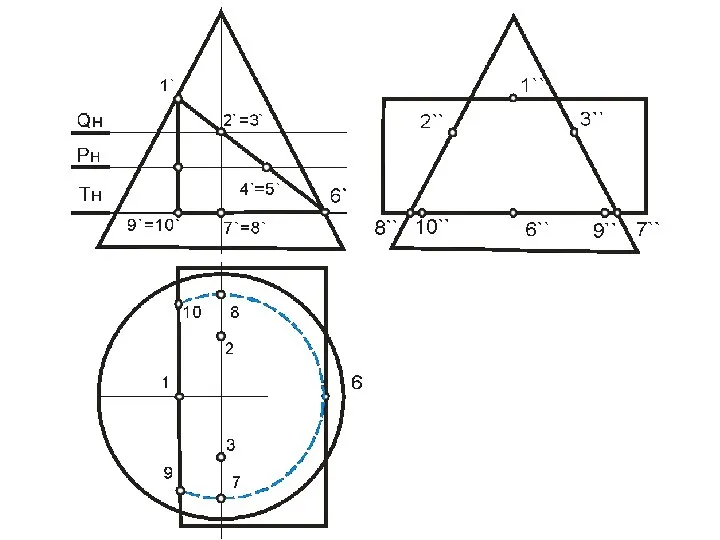
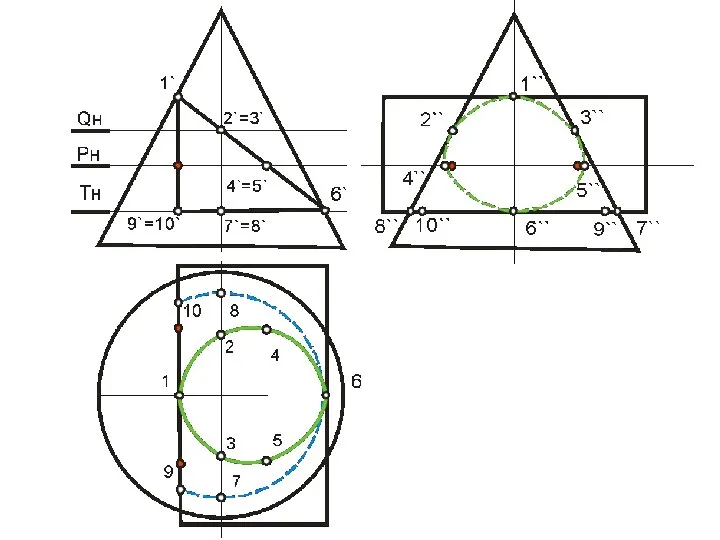
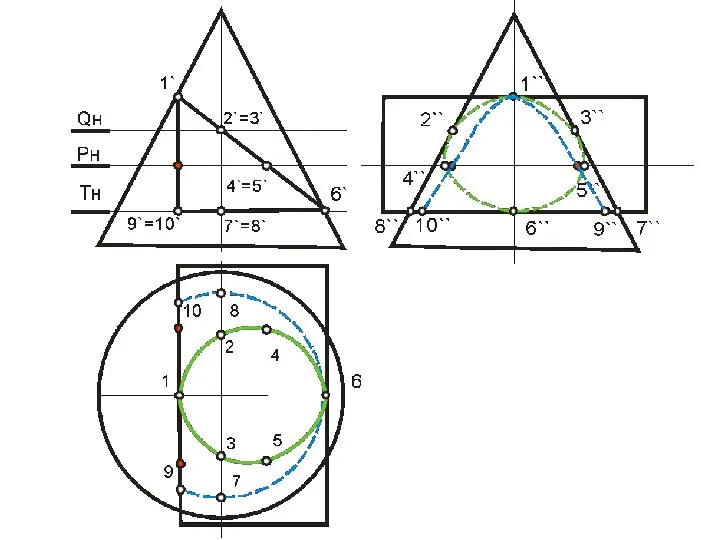
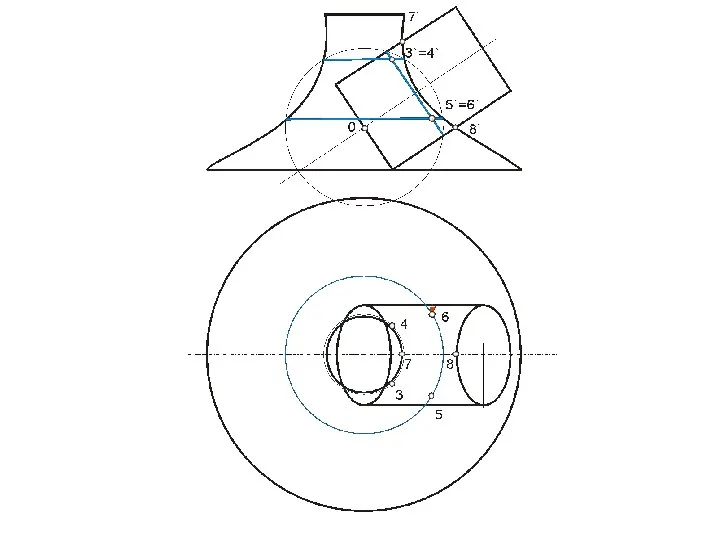
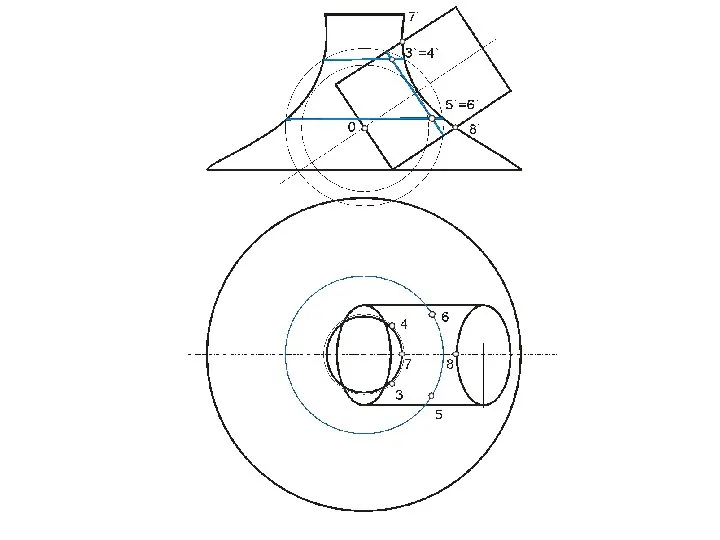
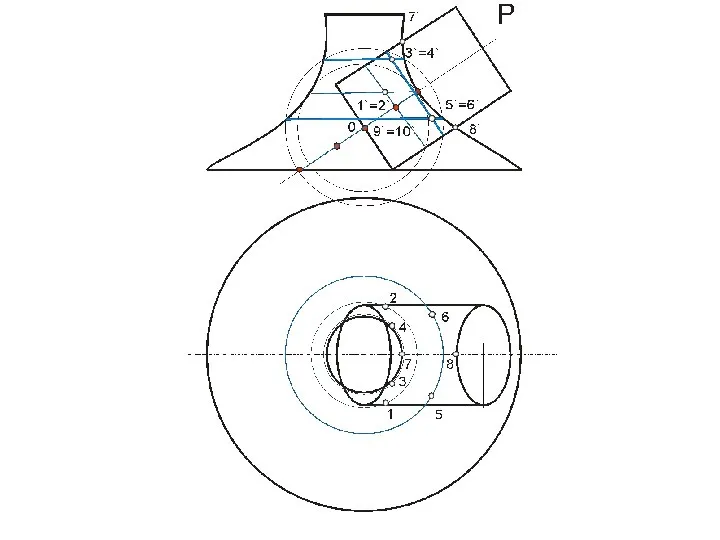
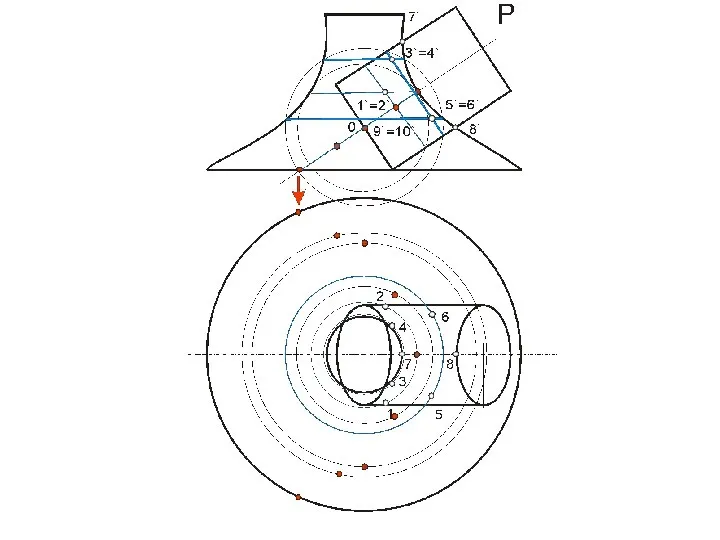
- 99. В этом случае призму можно рассматривать, как три плоскости α, β, γ, проходящие через ее грани,
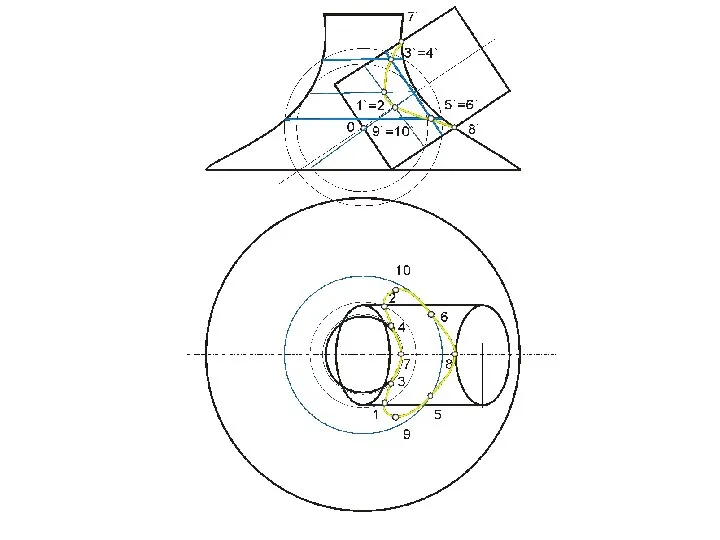
- 112. Точки 12 и 62 – пересечения плоскости γ с очерком проекции конуса на плоскость П2 (главным
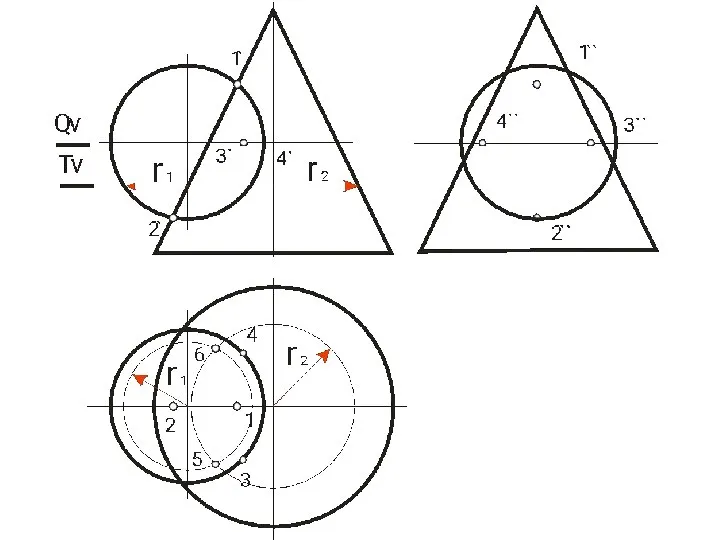
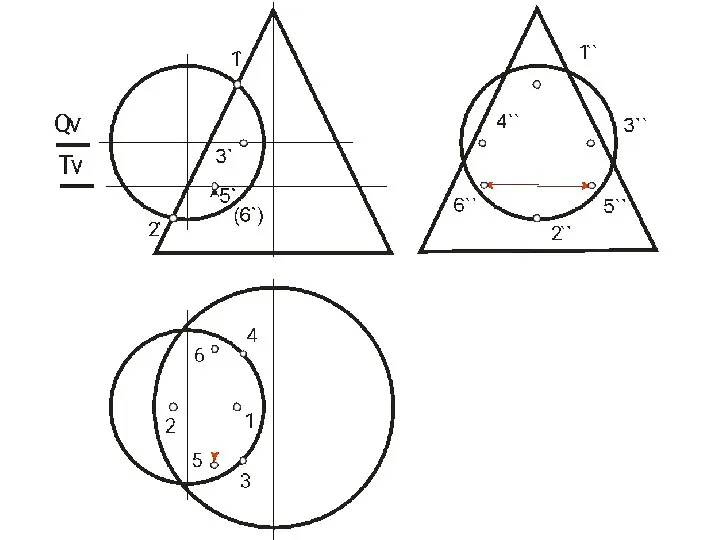
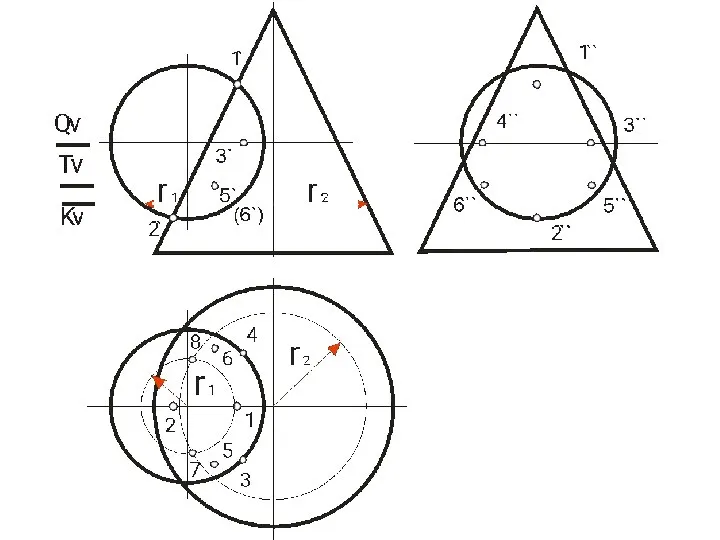
- 113. МЕТОД СЕКУЩИХ СФЕР Способ секущих сфер с постоянным центром для построения линии пересечения двух поверхностей применяют
- 114. Алгоритм 1) За центр выбираем точку пересечения осей. 2) С данной точки проводим сферу, чтобы она
- 115. МЕТОД СЕКУЩИХ СФЕР
- 128. Каждая из этих поверхностей имеет семейство окружностей, являющихся линиями сечения их концентрическими сферами. Применению метода концентрических
- 129. Оси поверхностей G и Q параллельны фронтальной плоскости проекций и пересекаются в точки А. Эта точка
- 130. Для точного построения линии пересечения поверхностей необходимо найти точки 9 и 10, которые определяют границу зоны
- 140. ЧАСТНЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА Поверхностью второго порядка называется множество точек пространства, декартовы координаты, которых
- 141. Теорема 1. Если две поверхности второго порядка пересекаются по одной плоской кривой, то существует и другая
- 142. Теорема 1
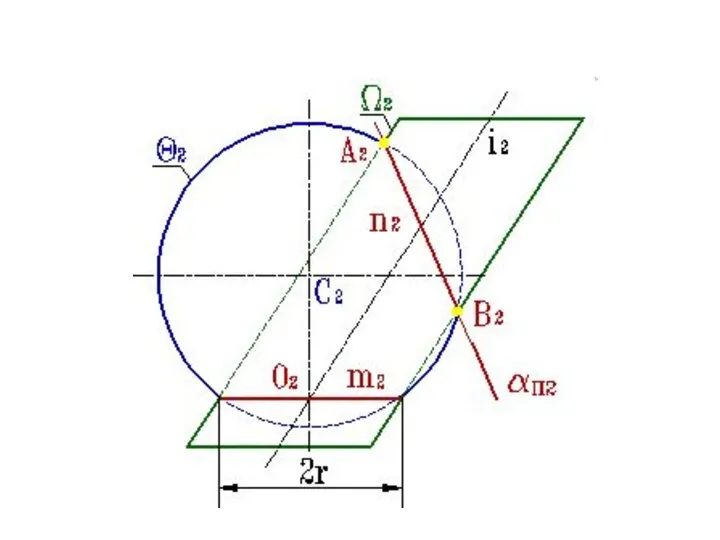
- 144. Теорема 1 Фронтальные проекции q2 сферы Q и W2 эллиптического цилиндра W, имеющих общую окружность m(m2)
- 145. Теорема 1 Плоскость σ, определяемая центром сферы С и осью i цилиндра, является плоскостью симметрии заданных
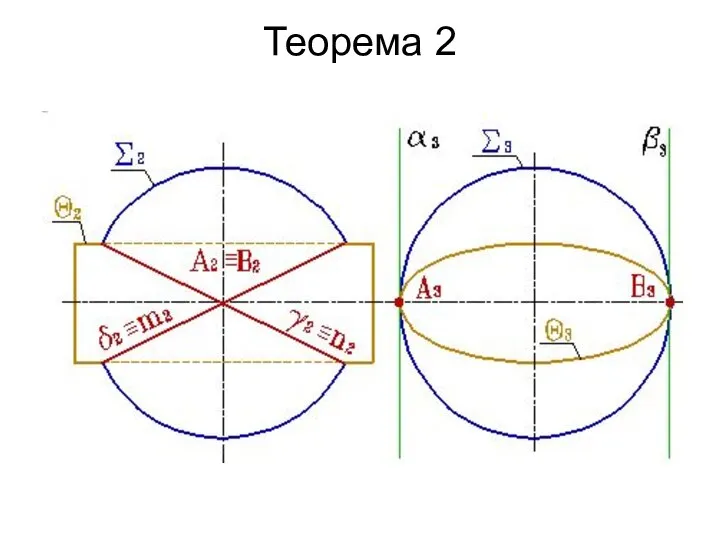
- 146. Теорема 2 Теорема 2.(о двойном касании). Если две поверхности второго порядка имеют касание в двух точках
- 147. Теорема 2
- 148. Теорема 2
- 149. Теорема 2 Например, по двум окружностям m и n пересекается сфера S и эллиптический цилиндр Q.
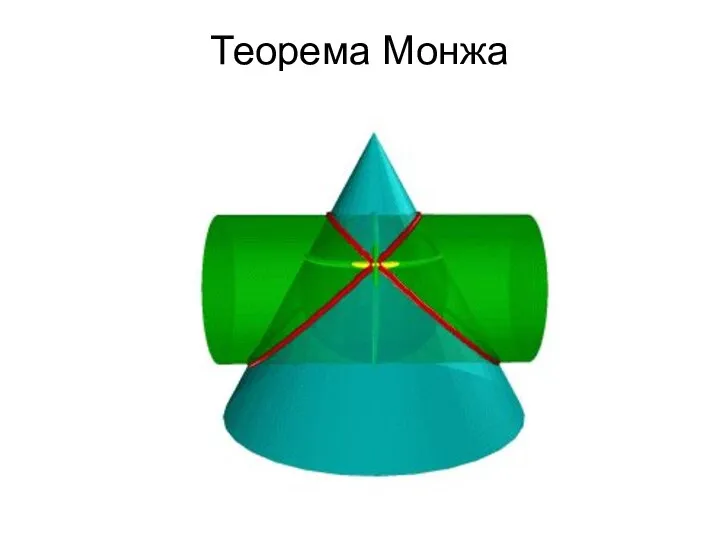
- 150. Теорема Монжа Теорема 3. (теорема Г. Монжа). Если две поверхности второго порядка описаны около третьей или
- 151. Теорема Монжа
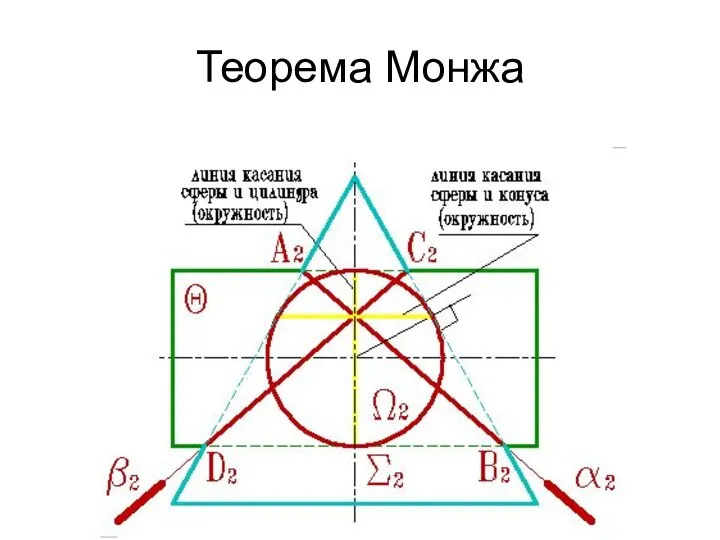
- 152. Теорема Монжа
- 153. В соответствии с этой теоремой линия пересечения конуса Σ и цилиндра Q, описанных около сферы W,
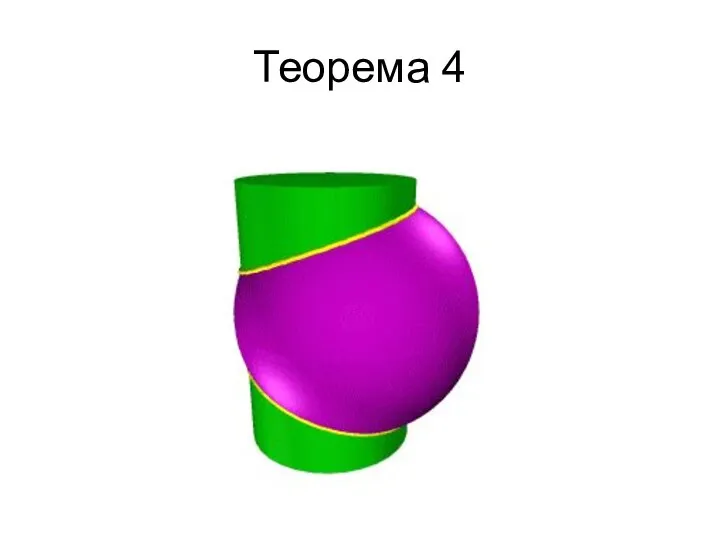
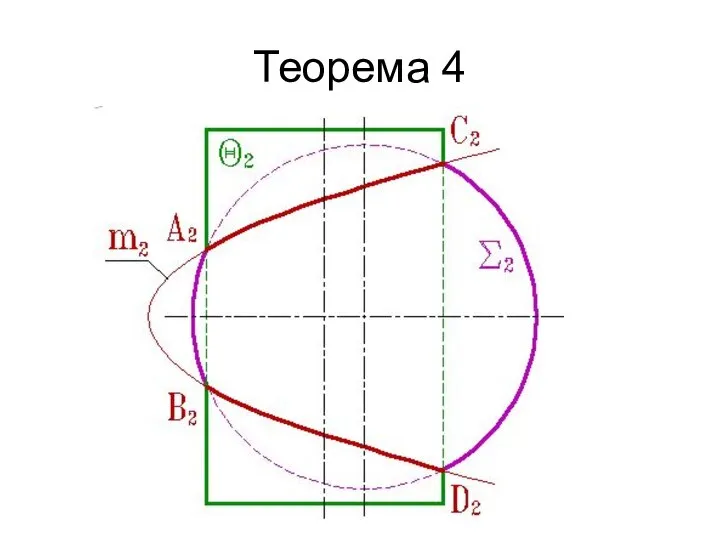
- 154. Теорема 4 Теорема 4. Если две поверхности второго порядка имеют общую плоскость симметрии, то линия их
- 155. Теорема 4
- 156. Теорема 4
- 158. Скачать презентацию


















































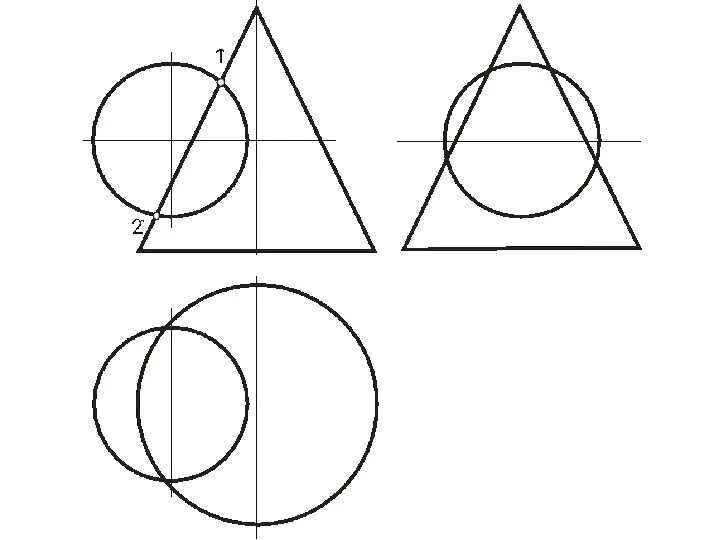

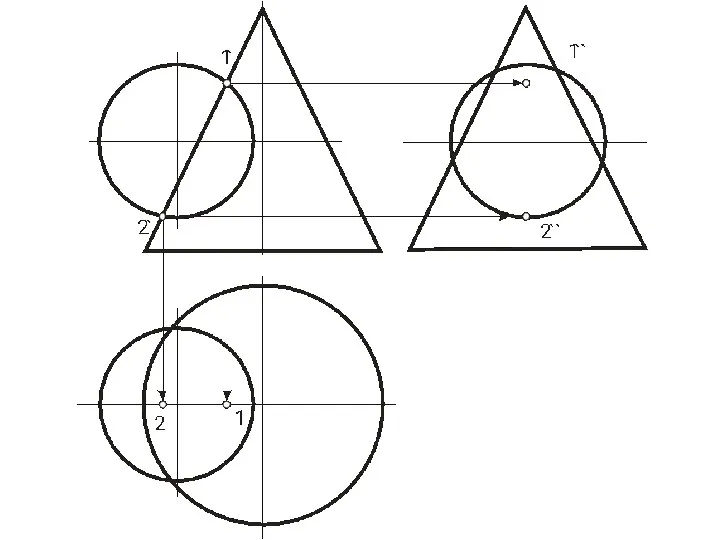
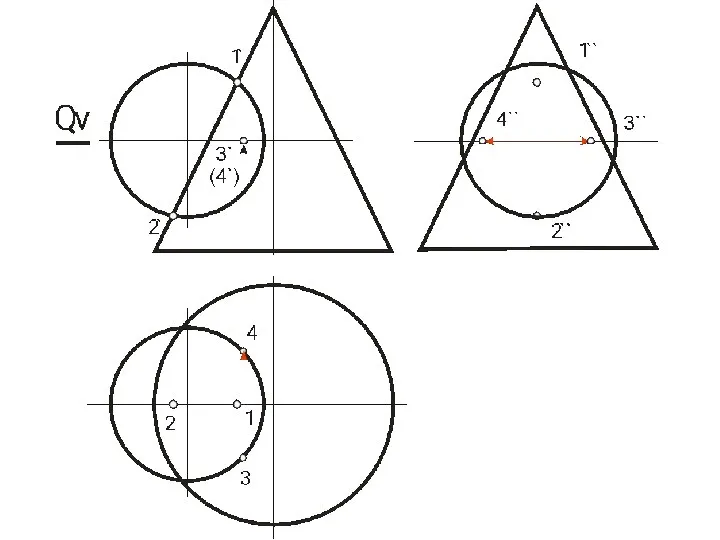




















 Связь между числами при делении. Проверка деления
Связь между числами при делении. Проверка деления Создание статичной или динамичной композиции из прямоугольников и линий
Создание статичной или динамичной композиции из прямоугольников и линий Алгоритм. Свойства алгоритма
Алгоритм. Свойства алгоритма Дежурный звук Н. Разложение многочлена на множители
Дежурный звук Н. Разложение многочлена на множители Решение задач по теме «Векторы». 9 класс
Решение задач по теме «Векторы». 9 класс Презентация Свойства числовых неравенств (8 класс)
Презентация Свойства числовых неравенств (8 класс)  Задачи с величинами: цена, количество, стоимость
Задачи с величинами: цена, количество, стоимость Презентация на тему Число и цифра 9
Презентация на тему Число и цифра 9  Алгебраические уравнения. (Лекция 1)
Алгебраические уравнения. (Лекция 1) Презентация по математике "Километр" - скачать бесплатно
Презентация по математике "Километр" - скачать бесплатно Математическое лото
Математическое лото Золотое сечение в архитектуре, скульптуре, живописи
Золотое сечение в архитектуре, скульптуре, живописи Системы линейных уравнений. Основные понятия
Системы линейных уравнений. Основные понятия Занимательные задачи 5 класс
Занимательные задачи 5 класс Стандартный вид числа
Стандартный вид числа Гоночная трасса, как пример мультиграфа
Гоночная трасса, как пример мультиграфа Решение задач
Решение задач Формирование УУД в процессе обучения математике
Формирование УУД в процессе обучения математике Игра-тренажёр «В гостях у ёжика» (математика 1 класс)
Игра-тренажёр «В гостях у ёжика» (математика 1 класс) Презентация по математике "Десятичные дроби" - скачать
Презентация по математике "Десятичные дроби" - скачать  Упрощение выражений
Упрощение выражений Сфера. Сфеерическая геометрия
Сфера. Сфеерическая геометрия Применение интеграла к решению физических задач
Применение интеграла к решению физических задач Деловая игра «Следствие ведут знатоки» - Презентация по математике_
Деловая игра «Следствие ведут знатоки» - Презентация по математике_ Криптографическая защита информации. Элементы теории чисел. (Лекция 3)
Криптографическая защита информации. Элементы теории чисел. (Лекция 3) Алгебра 9 класс Учитель: Романова Т.А.
Алгебра 9 класс Учитель: Романова Т.А.  Решение задач на множества
Решение задач на множества Упрощение выражений. Математика 5 класс. Гимнастика ума
Упрощение выражений. Математика 5 класс. Гимнастика ума