Содержание
- 2. Определение 1: Пусть функция y = f (x) определена в некоторой окрестности точки x0. Число A
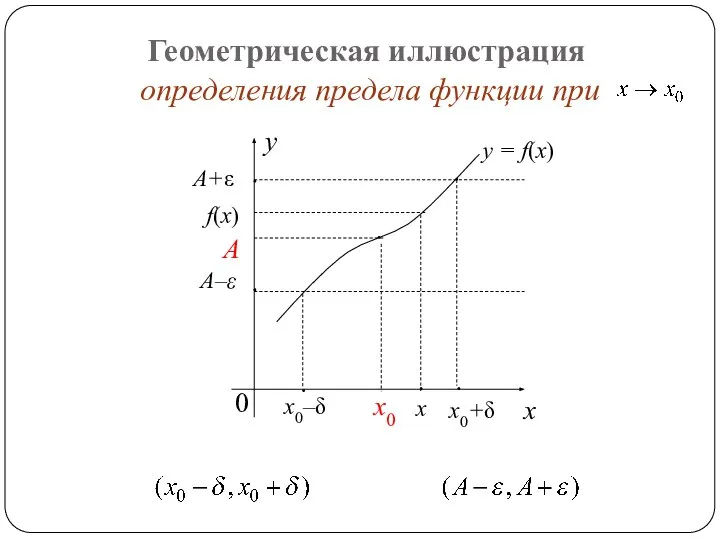
- 3. Геометрическая иллюстрация определения предела функции при
- 4. Определение 2: Число A называется пределом функции y = f (x) при , если для любого
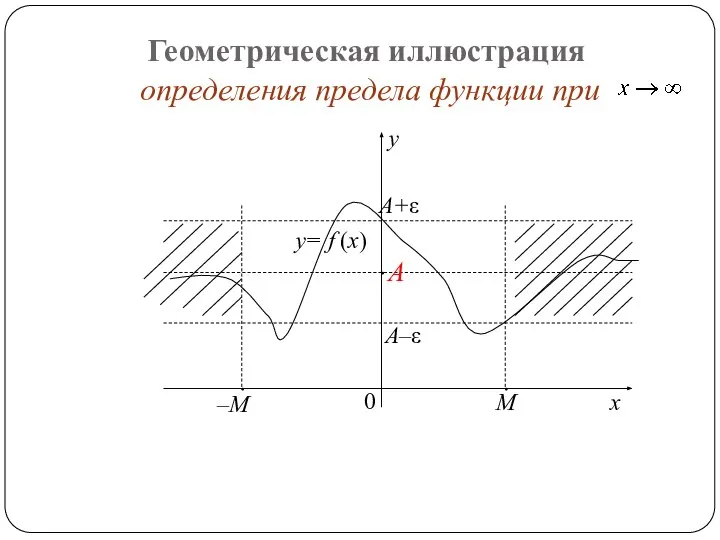
- 5. Геометрическая иллюстрация определения предела функции при y= f (x)
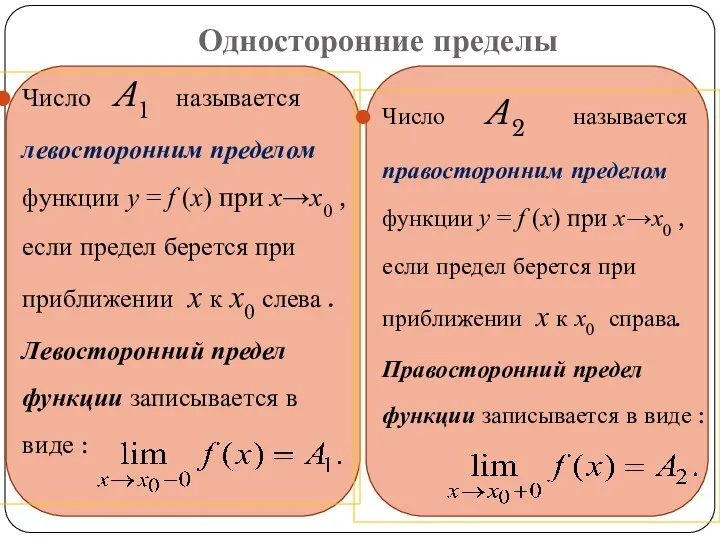
- 6. Односторонние пределы Число A1 называется левосторонним пределом функции y = f (x) при x→x0 , если
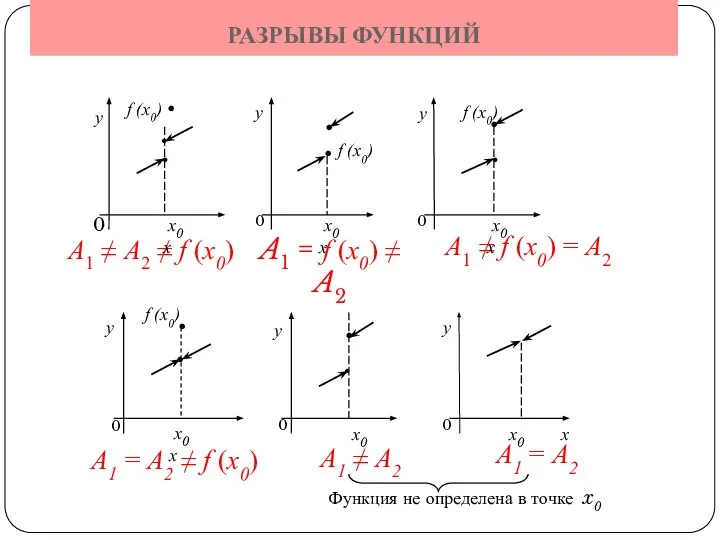
- 7. РАЗРЫВЫ ФУНКЦИЙ A1 ≠ A2 ≠ f (x0) A1 = f (x0) ≠ A2 A1 ≠
- 8. Теорема (существования предела) Для того, чтобы функция y = f (x) при x→x0 имела пределом число
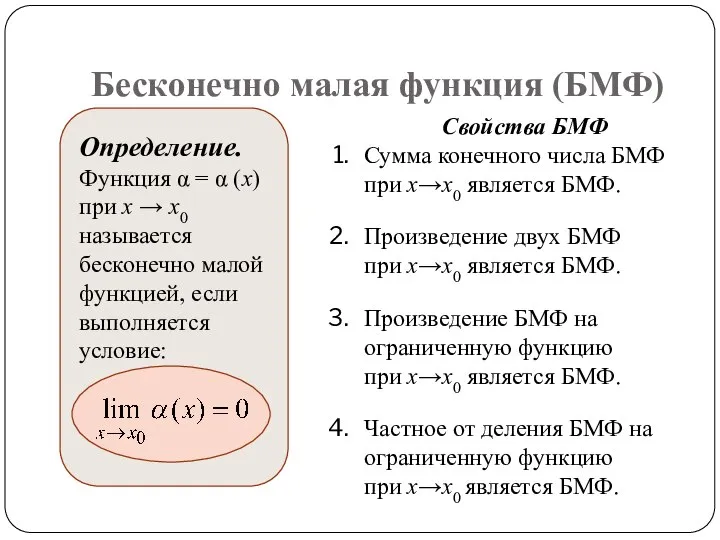
- 9. Бесконечно малая функция (БМФ) Определение. Функция α = α (x) при x → x0 называется бесконечно
- 10. Сравнение БМФ Определение 1. Две БМФ α1(x) и α2(x) называются эквивалентными при x→x0 , если выполняется
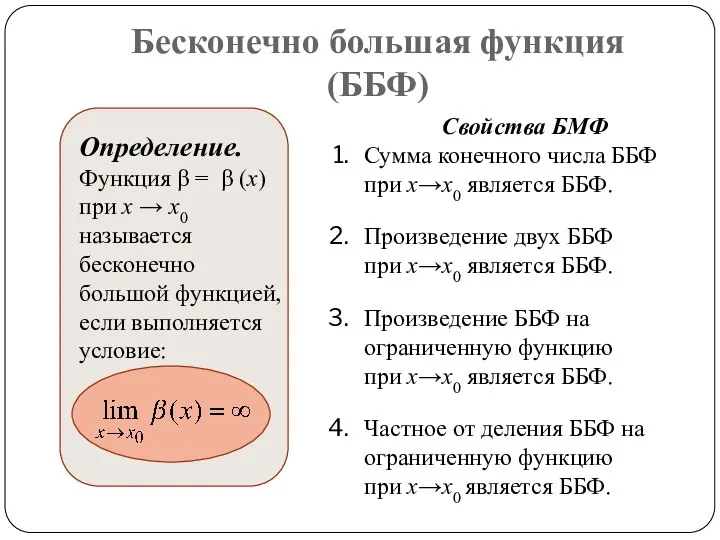
- 11. Бесконечно большая функция (ББФ) Определение. Функция β = β (x) при x → x0 называется бесконечно
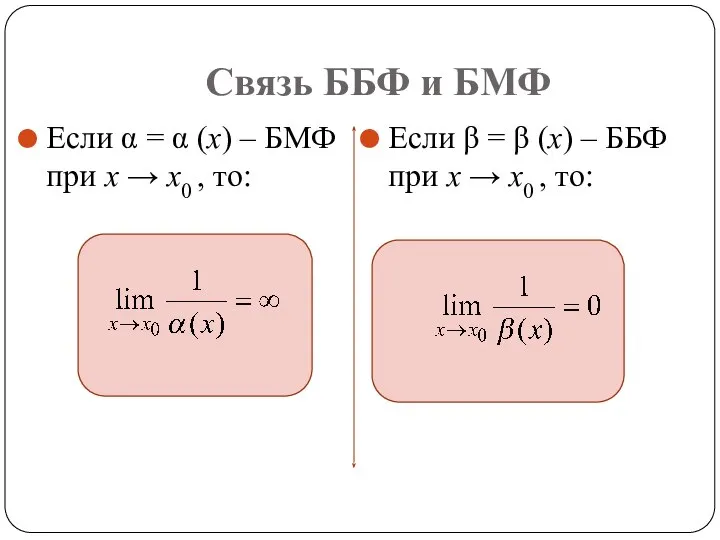
- 12. Связь ББФ и БМФ Если α = α (x) – БМФ при x → x0 ,
- 14. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ.
- 15. Основные теоремы о пределах Теорема 1. Всякая функция y = f (x) при x→x0 может иметь
- 16. ТЕОРЕМА 3. Замечательные пределы Первый замечательный: (раскрывает неопределенность 0/0) Второй замечательный: (раскрывает неопределенность )
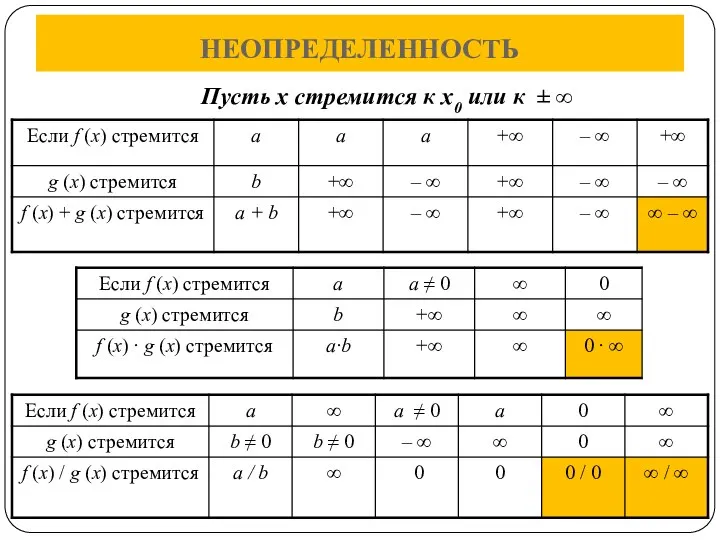
- 17. НЕОПРЕДЕЛЕННОСТЬ Пусть х стремится к х0 или к ± ∞
- 18. АЛГОРИТМ ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ ФУНКЦИЙ Используя правило предельного перехода вычисляем предел функции, подставляя в нее предельное значение
- 19. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ Если находим предел дробного выражения, в числителе и знаменателе которого многочлен и имеем неопределенность
- 20. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ 2) Если находим предел дробно-иррационального выражения и имеем неопределенность 0 / 0, то для
- 21. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ 3) Если находим предел дробного выражения в числители и знаменателе которого могут встречаться тригонометрические,
- 22. sin α(x) ~ α (x); 2) tg α(x) ~ α (x); arcsin α(x) ~ α (x);
- 23. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ 4. Если находим предел дробно-рационального и дробно-иррационального выражения и имеем неопределенность ∞ / ∞,
- 24. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ 5. Если находим предел алгебраического выражения и имеем неопределенность 0∙ ∞ или ∞ -
- 25. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ 6. Если находим предел алгебраического выражения и имеем неопределенность , то для раскрытия данной
- 26. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ 7. Если находим предел алгебраического выражения и имеем неопределенность , то для раскрытия данных
- 28. Скачать презентацию
















 Презентация по математике "«Упрощение выражений» 5 класс" - скачать бесплатно_
Презентация по математике "«Упрощение выражений» 5 класс" - скачать бесплатно_ Показательная функция
Показательная функция Алгебра. Лекция 6. Классы вычетов
Алгебра. Лекция 6. Классы вычетов Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными Нахождение дроби от числа и процентов от числа.
Нахождение дроби от числа и процентов от числа. Презентация на тему Усеченный конус
Презентация на тему Усеченный конус Свойства сложения
Свойства сложения Статистические показатели
Статистические показатели Тема: «Решение примеров и задач изученных видов» 5 класс Учитель: А.В.Лисицинская
Тема: «Решение примеров и задач изученных видов» 5 класс Учитель: А.В.Лисицинская Пропорция
Пропорция Построение графика функции
Построение графика функции Задачи на перебор вариантов
Задачи на перебор вариантов Классы интегрируемых функций. Интегрирование иррациональных выражений
Классы интегрируемых функций. Интегрирование иррациональных выражений Методы простых средних и скользящих средних
Методы простых средних и скользящих средних Учимся определять время по часам
Учимся определять время по часам Сложение чисел с разными знаками
Сложение чисел с разными знаками Готовимся к ОГЭ по математике, решение задания №24
Готовимся к ОГЭ по математике, решение задания №24 Подготовка к контрольной работе по теме «Системы линейных уравнений»
Подготовка к контрольной работе по теме «Системы линейных уравнений» Задачи на разрезание и перекраивание фигур
Задачи на разрезание и перекраивание фигур Аттестационная работа. Может ли нам комбинаторика помочь в реальной жизни
Аттестационная работа. Может ли нам комбинаторика помочь в реальной жизни Действия с натуральными числами. Урок-сказка
Действия с натуральными числами. Урок-сказка Многочлени. Узагальнення знання учнів
Многочлени. Узагальнення знання учнів Рациональные числа как бесконечные десятичные периодические дроби
Рациональные числа как бесконечные десятичные периодические дроби Решение задач на проценты
Решение задач на проценты Занимательная математика
Занимательная математика Умножение многозначных круглых чисел
Умножение многозначных круглых чисел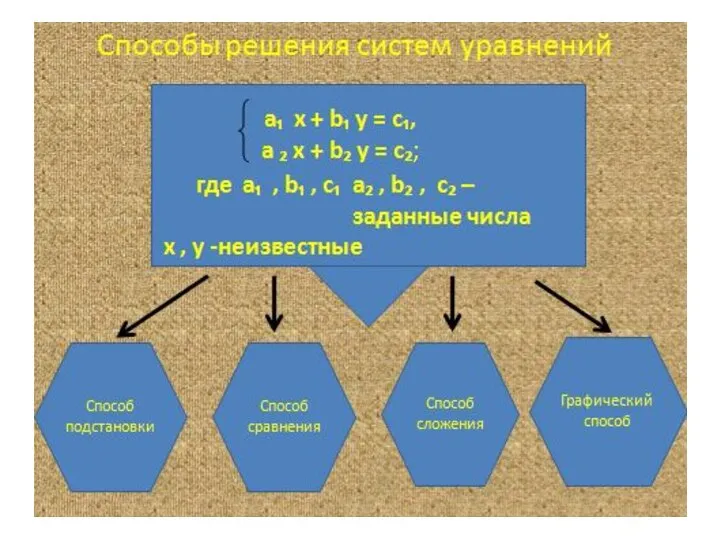 Способы решения систем уравнений (4)
Способы решения систем уравнений (4) Аттестационная работа. Образовательная программа по внеурочной деятельности «Наглядная геометрия»
Аттестационная работа. Образовательная программа по внеурочной деятельности «Наглядная геометрия»