Содержание
- 3. Примеры решение задач (№24-25) из Демо-версии 2018 года
- 5. 2. Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и
- 6. Решение: Рассмотрим четырехугольник PKBC. PKBC вписан в окружность, следовательно выполняется условие: сумма противоположных углов четырехугольника равна
- 7. 3. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга
- 8. Решение: 1.Треугольник ACO прямоугольный по свойству касательной (радиус к ней перпендикулярен). Угол AOD центральный и равен
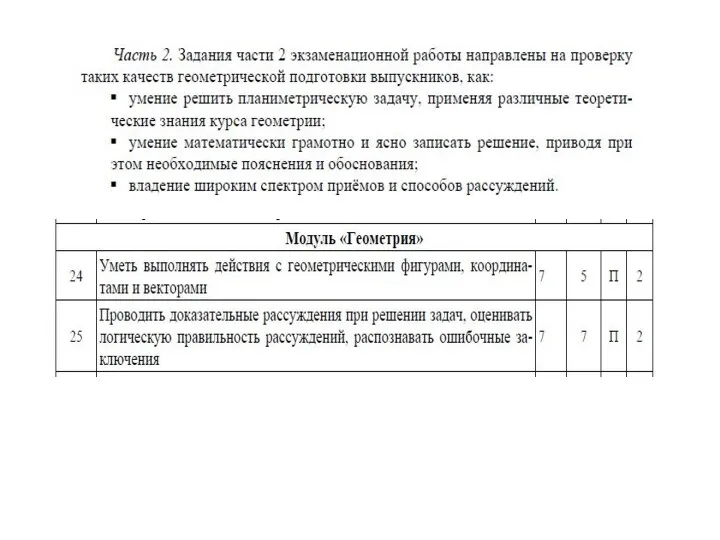
- 9. 4. В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между
- 10. Решение: 1. BD - биссектриса => угол СBD = 1/2 АВС = 1/2 *(180° - (40°+60°))
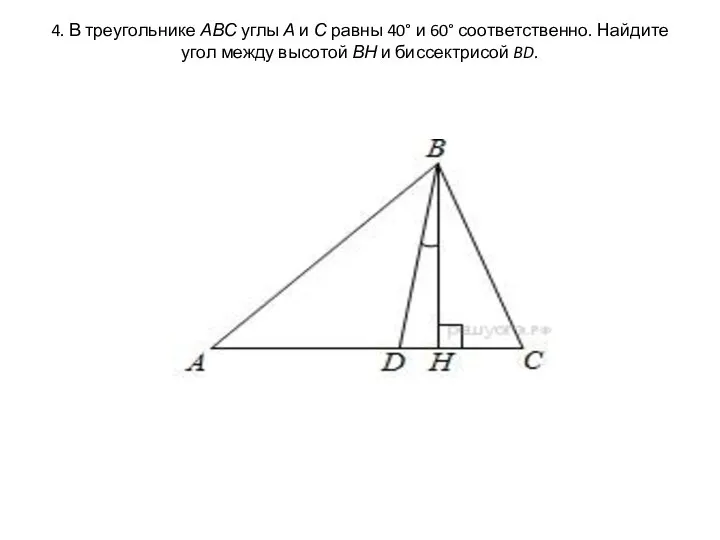
- 11. 5. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите
- 12. Решение: BC||AD (по определению параллелограмма) ∠BAE=∠EAD (т.к. AE - биссектриса) ∠EAD=∠BEA (т.к. это накрест-лежащие углы) Следовательно,
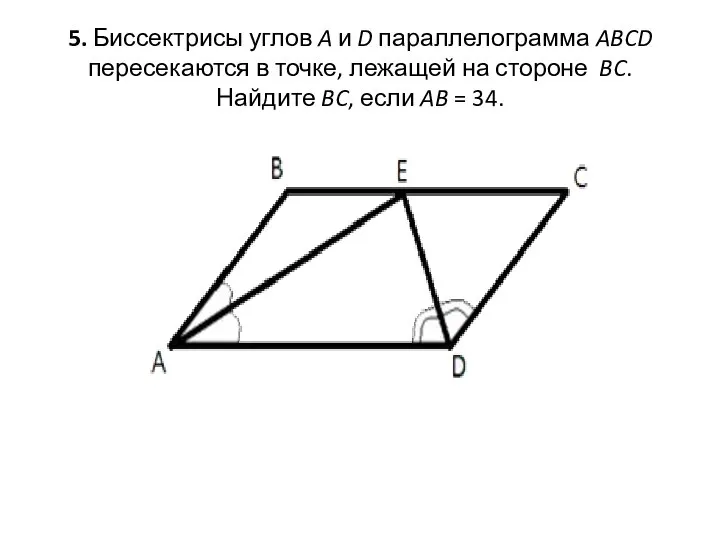
- 13. 6. Высота AH ромба ABCD делит сторону CD на отрезки DH = 12 и CH =
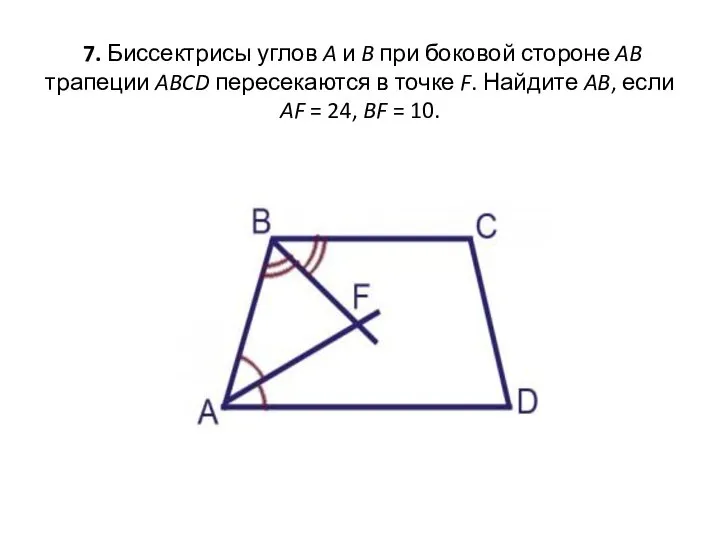
- 14. 7. Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F.
- 15. Решение: 1. Углы BAD и ABC — внутренние односторонние при прямых AD || BC и секущей
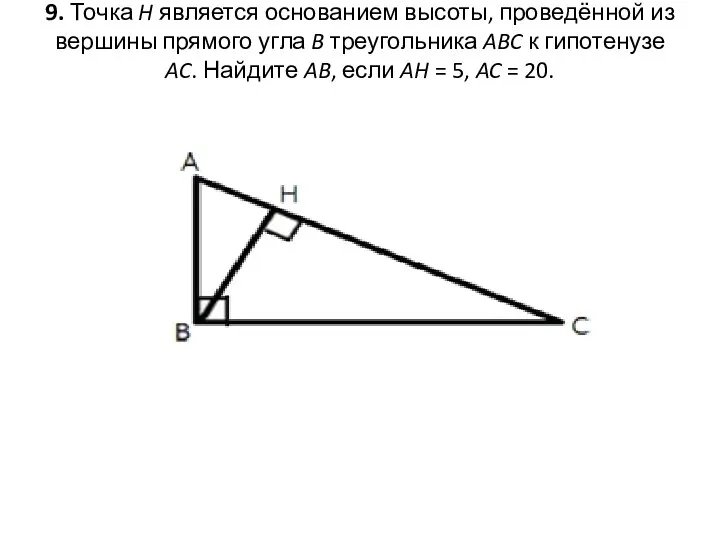
- 16. 9. Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе
- 17. Решение: 1.Рассмотрим треугольники ABC и ABH. ∠A – общий, ∠AHB=∠ABC .Следовательно, эти треугольники подобны (по признаку
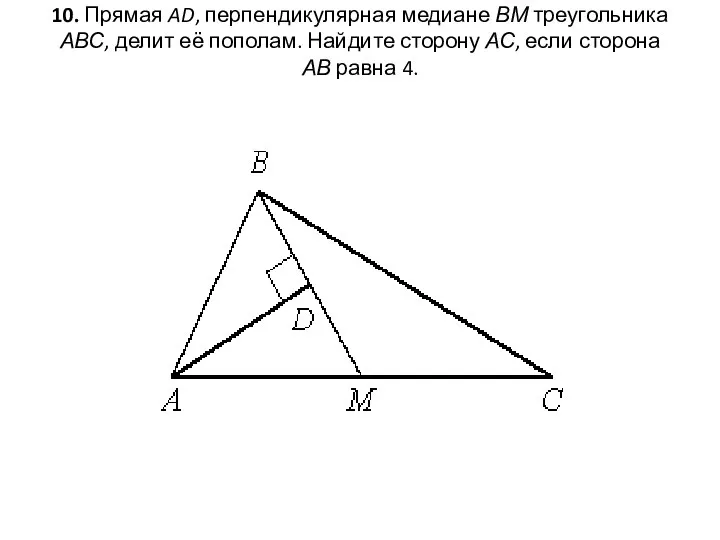
- 18. 10. Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона
- 19. Решение: 1. AD для треугольника ABM является и медианой, и высотой. А это свойство медианы для
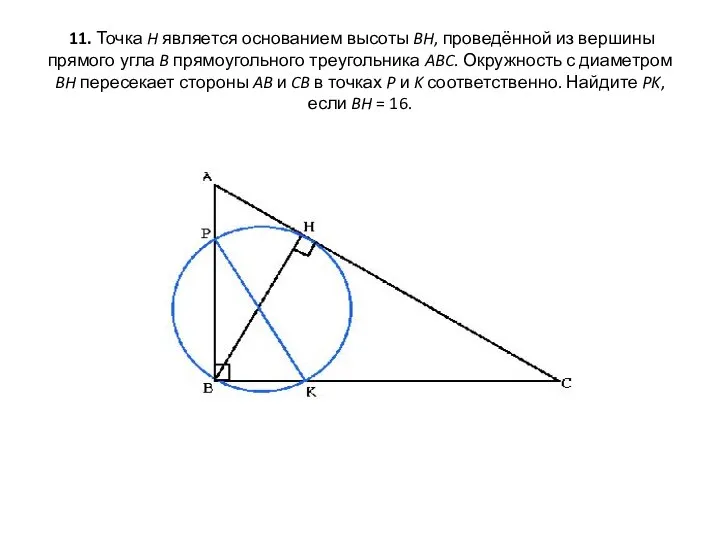
- 20. 11. Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC.
- 21. Решение: 1.Вписанный угол РВК - прямой по условию задачи. Так как центральный угол равен двум прямым
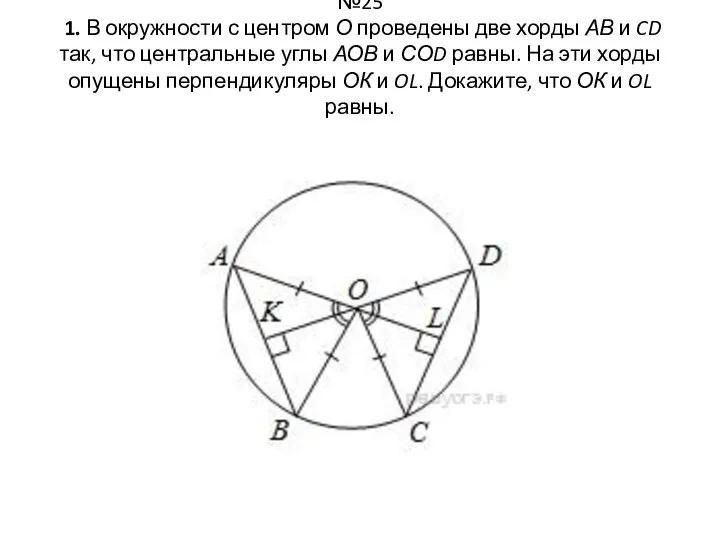
- 22. №25 1. В окружности с центром О проведены две хорды АВ и CD так, что центральные
- 23. Доказательство: Треугольники АОВ и СОD равны по двум сторонам и углу между ними (AO = BO
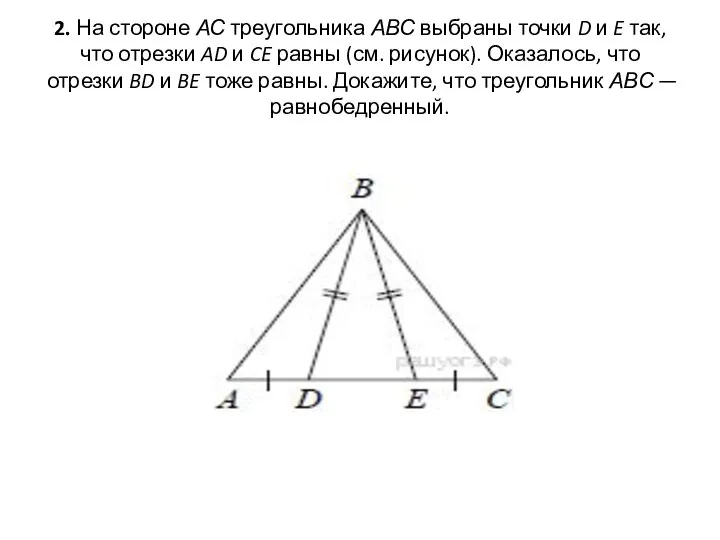
- 24. 2. На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и
- 25. Доказательство: По условию задачи BD=BE, следовательно треугольник BDE - равнобедренный (по определению). По свойству равнобедренного треугольника
- 26. 3. В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC
- 27. Доказательство: 1.∠АBD и ∠ACD опираются на отрезок AD и равны друг другу. Значит мы можем провести
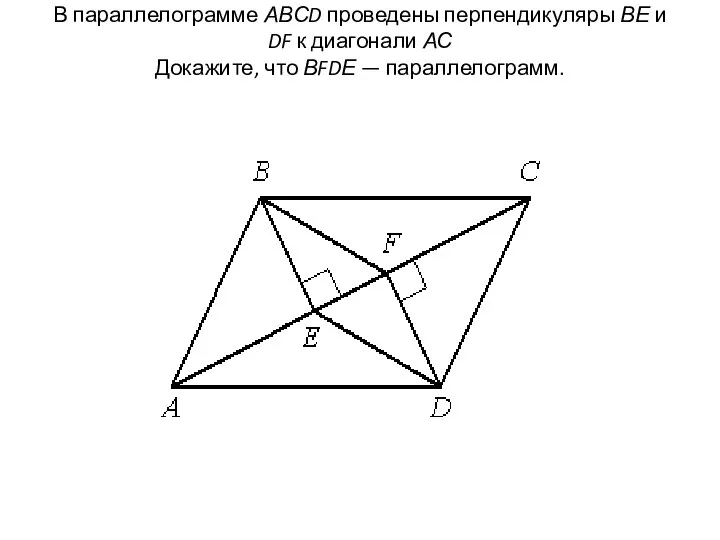
- 28. В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС Докажите, что ВFDЕ — параллелограмм.
- 29. Доказательство: 1) Рассмотрим треугольники ABE и CDF. AB=CD (по свойству параллелограмма). Угол BAE = углу DCF
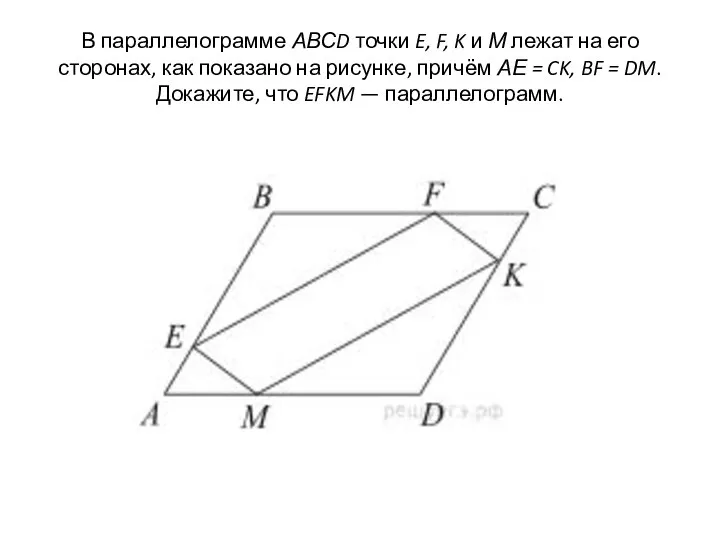
- 30. В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на
- 31. Доказательство: Угол А= углуС (т.к. АВСД паралелограмм), АЕ=СК, АМ=FC (по условию задачи), значит треугольник AME =
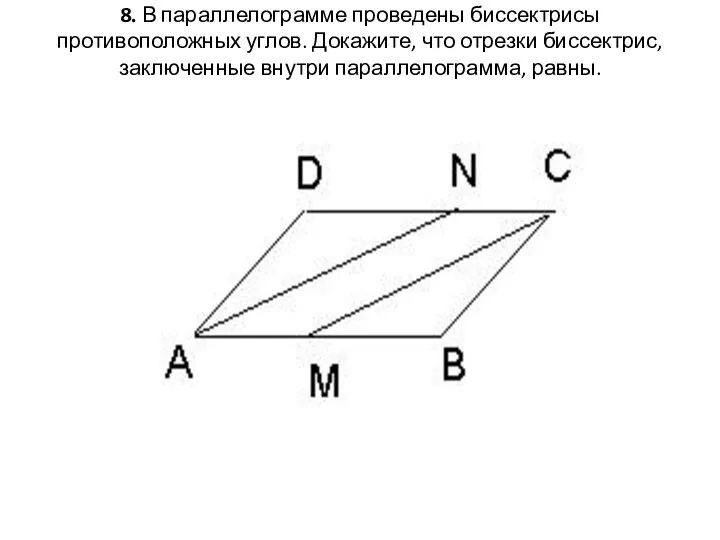
- 32. 8. В параллелограмме проведены биссектрисы противоположных углов. Докажите, что отрезки биссектрис, заключенные внутри параллелограмма, равны.
- 33. Доказательство: 1. Рассмотрим треугольники ADN и CBM AD = DC как противоположные стороны параллелограмма, 2. Угол
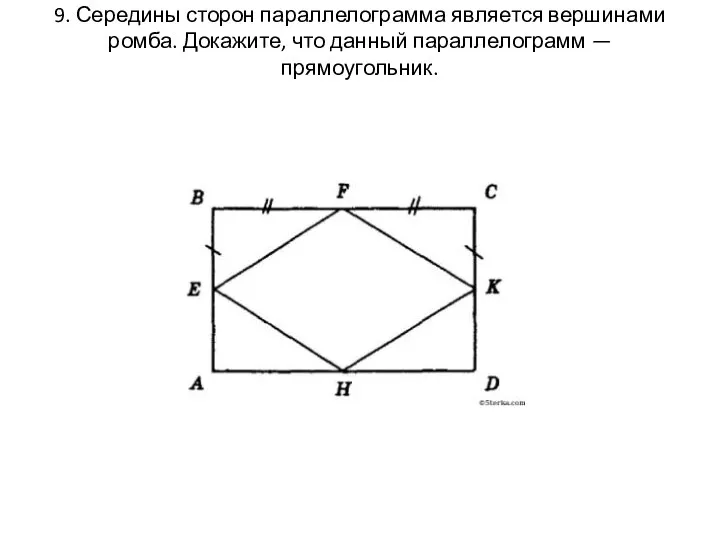
- 34. 9. Середины сторон параллелограмма является вершинами ромба. Докажите, что данный параллелограмм — прямоугольник.
- 35. Доказательство: Рассмотрим треугольники AEH и BEF: 1.ВЕ = ВA так как Е – середина АВ 2.
- 37. Скачать презентацию




















 Перпендикуляр и наклонные. Задачи на готовых чертежах
Перпендикуляр и наклонные. Задачи на готовых чертежах Матриці та дії над ними
Матриці та дії над ними Проценты. Устная работа
Проценты. Устная работа История появления функции
История появления функции Пифагор Самосский
Пифагор Самосский Круглые числа
Круглые числа Вычитание и сложение. (Урок 13)
Вычитание и сложение. (Урок 13) Устная работа. Логарифмы. 10 класс
Устная работа. Логарифмы. 10 класс Презентация по математике "Решение задач по нахождению величин по сумме и разности" - скачать бесплатно
Презентация по математике "Решение задач по нахождению величин по сумме и разности" - скачать бесплатно Отношения на множествах
Отношения на множествах Матрицы. Определения
Матрицы. Определения Исследование функций с помощью производной
Исследование функций с помощью производной Число π
Число π Абсолютті және қатысты шамалар
Абсолютті және қатысты шамалар Теория вероятностей на ЕГЭ по математике
Теория вероятностей на ЕГЭ по математике Геометрические характеристики плоского составного сечения
Геометрические характеристики плоского составного сечения Презентация по математике "Кроссворд по математике" - скачать бесплатно
Презентация по математике "Кроссворд по математике" - скачать бесплатно Сложение и вычитание целых чисел. 6 класс
Сложение и вычитание целых чисел. 6 класс Алгоритмическое и программное обеспечение для решения задач обработки статистической информации
Алгоритмическое и программное обеспечение для решения задач обработки статистической информации Algebra. Natural Integers rational Numbers
Algebra. Natural Integers rational Numbers Методы математической морфологии при обработке изображений
Методы математической морфологии при обработке изображений Саннар. Чама саны приблизительные числительные
Саннар. Чама саны приблизительные числительные Треугольник. Периметр
Треугольник. Периметр Вопросы к экзамену
Вопросы к экзамену Основні правила комбінаторики
Основні правила комбінаторики Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Сумма углов треугольника. Работа с чертежами
Сумма углов треугольника. Работа с чертежами Сюжетные задачи
Сюжетные задачи