Содержание
- 2. Связность Пусть G =(V, E) – н-граф. Связными называются вершины a и b если существуют маршрут,
- 3. Связность Утверждение: отношение связности является отношением эквивалентности. Доказательство: 1.Каждая вершина связана сама с собой маршрутом нулевой
- 4. Связность 2. Если вершина a связна с b, то и b связна с a. Если a
- 5. Связность 3. Если вершина a связана маршрутом с b, b связана с с, то и a
- 6. Связность Отношение рефлексивно, симметрично и транзитивно, значит является отношением эквивалентности. Множество вершин V разбивается отношением связности
- 7. Связность Связными компонентами графа G называются подграфы, порожденные классами эквивалентности по отношению связности. Замечание: В связном
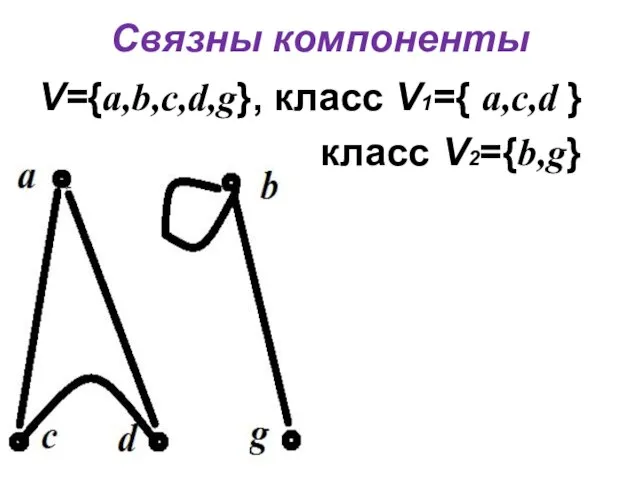
- 8. Связны компоненты V={a,b,c,d,g}, класс V1={ a,c,d } класс V2={b,g}
- 9. Разделяющие множества Разделяющим множеством н-графа G =(V, E) называется множество ребер, при удалении которых число компонент
- 10. Разделяющие множества Разрезом в н-графе G =(V, E) называется разделяющее множество в котором нет лишних ребер,
- 11. Разделяющие множества Мостом или перешейком в н-графе G =(V, E) называется разрез, состоящий из одного ребра.
- 12. Разделяющие множества Разделяющее множество {(1,4), (2,3), (7,8)}; Разрез {(1,4), (2,3)}, (7,8) – лишнее; Мост {(4,5).
- 13. Шарнир Вершина - н-графа G =(V, E) называется шарниром, если удаление этой вершины и всех инцидентных
- 15. Скачать презентацию











 Ұшқыр ойлы жҰлдыздар. Ителлектуалды сайыс
Ұшқыр ойлы жҰлдыздар. Ителлектуалды сайыс Презентация по математике "Решение уравнений с использованием графической модели" - скачать
Презентация по математике "Решение уравнений с использованием графической модели" - скачать  Умножение и деление обыкновенных дробей. Математический диктант
Умножение и деление обыкновенных дробей. Математический диктант Основы статистики. Магия цифр: когда стоит сомневаться в статистике?
Основы статистики. Магия цифр: когда стоит сомневаться в статистике? Сводка и группировка материалов статистического наблюдения
Сводка и группировка материалов статистического наблюдения Решение задач на проценты
Решение задач на проценты Иррациональные уравнения
Иррациональные уравнения Математическая шифровка
Математическая шифровка Сложение векторов
Сложение векторов Повторение по теме: «Натуральные числа»
Повторение по теме: «Натуральные числа» Презентация Переменные процентные ставки В течение периода времени действует ставка простых процентов Начисленные проценты составят: В течение периода времени действует ставка простых процентов Начисленные проценты составят: ………………………………………
Презентация Переменные процентные ставки В течение периода времени действует ставка простых процентов Начисленные проценты составят: В течение периода времени действует ставка простых процентов Начисленные проценты составят: ………………………………………  Планиметрия в вопросах и ответах
Планиметрия в вопросах и ответах Логические задачи
Логические задачи Конус. Конические сечения
Конус. Конические сечения Презентация по математике "Экскурсия в мир чисел" - скачать
Презентация по математике "Экскурсия в мир чисел" - скачать  Бесконечность не предел
Бесконечность не предел Сумма углов треугольника. Лаборатория экспериментов
Сумма углов треугольника. Лаборатория экспериментов Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей ЕГЭ по математике 2012. (Часть 2)
ЕГЭ по математике 2012. (Часть 2) Умножение натуральных чисел и его свойства
Умножение натуральных чисел и его свойства Проверка и оценка знаний таблицы умножения и деления
Проверка и оценка знаний таблицы умножения и деления Системы рациональных неравенств
Системы рациональных неравенств Правильні многогранники
Правильні многогранники Прямоугольник. Квадрат
Прямоугольник. Квадрат Вычисление площади криволинейной трапеции
Вычисление площади криволинейной трапеции Геометрия. Виды треугольников
Геометрия. Виды треугольников Формула корней квадратного уравнения
Формула корней квадратного уравнения Смешанные дроби
Смешанные дроби