Содержание
- 2. 1. Верно ли утверждение: «прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей этой плоскости»
- 3. Дано: ABCD – параллелограмм, BD ⊥ α, АВ=7 см. Найдите Р АВCD. α B A D
- 4. В H С А ? α BH ⊥ α ?
- 7. Отрезок АВ длины a перпендикулярен плоскости. Точка А лежит в плоскости. В этой плоскости проведена прямая.
- 8. Iспособ Дано: BA⊥ α, AH ⊥ t Доказать: BH ⊥ t Доказательство: 1. Пусть BH не
- 9. Теорема о трёх перпендикулярах. Прямая, проведённая в плоскости через основание наклонной перпендикулярно к её проекции на
- 10. Теорема о трех перпендикулярах: Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на
- 11. III способ (свойства равнобедренного треугольника) Дано: SO ⊥ α, OA ⊥ t Доказать: SA ⊥ t
- 12. Назовите отрезок, длина которого равна расстоянию от т. М до выделенной прямой. Ответ обоснуйте. М D
- 13. Задача № 1 Дано: АВСК –прямоугольник. Доказать: C Задача № 154
- 14. Задача №154 (Атанасян) Прямая BD перпендикулярна к плоскости треугольника АВС. Известно, что BD = 9 см,
- 15. Задача № 3 Определите вид диагонального сечения куба.
- 16. B A C α a b Задача №4 Среди точек прямой b точка В является ближайшей
- 17. Задача №5 Назовите несколько прямых перпендикулярных диагонали куба. А1 D1 C1 B1 А D С В
- 18. Задача № 6 (145) Дано: Доказать: C
- 20. Скачать презентацию

















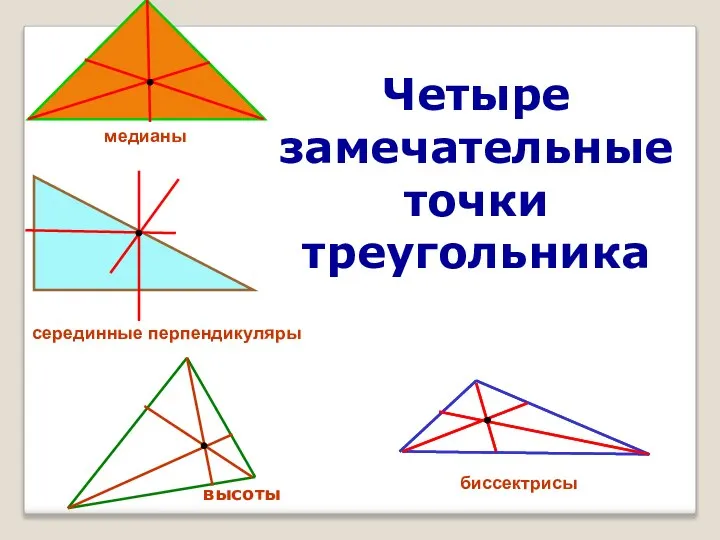 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Построение сечения плоскостью
Построение сечения плоскостью Площади многоугольников
Площади многоугольников Шкала. Координатный луч
Шкала. Координатный луч Измерение углов
Измерение углов Корреляционный и статистический анализ экспериментальных данных в программе Excel
Корреляционный и статистический анализ экспериментальных данных в программе Excel Коллекция картинок к урокам математики Часть 2
Коллекция картинок к урокам математики Часть 2 Теорема синусов Теорема косинусов Учитель математики Г.А.Ларькина Школа №91 г.Н.Новгород
Теорема синусов Теорема косинусов Учитель математики Г.А.Ларькина Школа №91 г.Н.Новгород  Коэффициент корреляции и корреляционный анализ
Коэффициент корреляции и корреляционный анализ 5 класс
5 класс  Соотношения между элементами прямоугольного треугольника
Соотношения между элементами прямоугольного треугольника Событие, вероятность события. Сложение и умножение вероятностей
Событие, вероятность события. Сложение и умножение вероятностей Системы линейных уравнений с двумя переменными
Системы линейных уравнений с двумя переменными Урок 11 Расстояния между прямыми
Урок 11 Расстояния между прямыми  Моделирование систем
Моделирование систем Открытый интенсив по математике. Как мощно подготовиться к экзамену? Ценность времени. День 2
Открытый интенсив по математике. Как мощно подготовиться к экзамену? Ценность времени. День 2 Исследование алфавита знаков для кодирования информации
Исследование алфавита знаков для кодирования информации Понятие вектора
Понятие вектора Повторительно-обобщающий урок по теме: «Показательная функция». 11 класс
Повторительно-обобщающий урок по теме: «Показательная функция». 11 класс Решение задач по теме "Векторы"
Решение задач по теме "Векторы" Сучасні методи моделювання в наукових дослідженнях
Сучасні методи моделювання в наукових дослідженнях Угол между прямыми. Подготовка к ЕГЭ С2
Угол между прямыми. Подготовка к ЕГЭ С2 Существование треугольника, равного данному
Существование треугольника, равного данному Пишите грамотно решение неполных квадратных уравнений
Пишите грамотно решение неполных квадратных уравнений Преобразование алгебраических выражений
Преобразование алгебраических выражений Презентация по математике Проценты
Презентация по математике Проценты  Оптимизация деятельности авторемонтного предприятия с помощью теории массового обслуживания
Оптимизация деятельности авторемонтного предприятия с помощью теории массового обслуживания Конус. Высота конуса
Конус. Высота конуса