Проблема эфира
Проблема эфира, который заполняет всё мироздание, волновала науку с давних
пор. В 1887 г. Майкельсон и Морли предприняли сложнейший для своего времени эксперимент по определению влияния движения Земли по орбите на скорость света .
В результате, никакого влияния обнаружено не было. Но чтобы это доказать и, главное, чтобы все в это поверили, скорость света следовало измерять с соответствующей точностью.
Попробуем её оценить. Скорость света: с=300000 км/с, а скорость движения Земли: v=30 км/с.
Из этих чисел видно, что абсолютная погрешность измерения скорости света не должна была превышать (3÷4) км/с. Много это или мало?
На этот вопрос отвечает другой способ определения точности измерений – относительная погрешность: ε=Δc/c. Из приведённых данных получаем ε=10-4, или одна сотая процента.
Значит, прежде, чем приступать к проведению столь сложного и дорогостоящего эксперимента, его авторы должны были убедиться, что это им по силам.
Кстати, современная точность определения скорости света: ε=10-9
Прежде, чем мы перейдём к другому примеру, отметим, что только что мы познакомились с двумя способами описания точности измерений: абсолютной и относительной погрешностями.
подробнее см. I стр. 7
.
Для науки







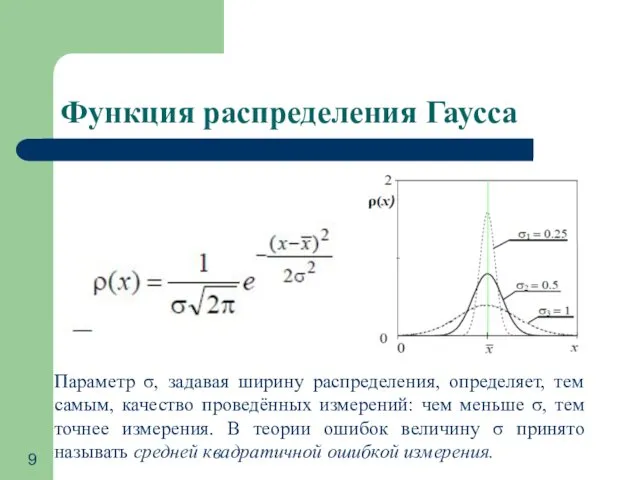
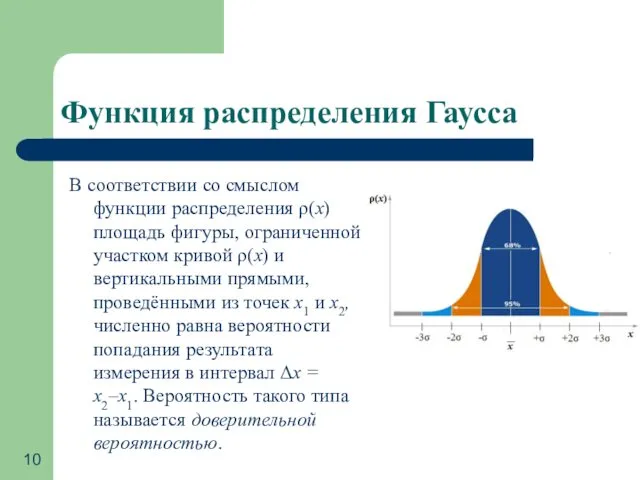







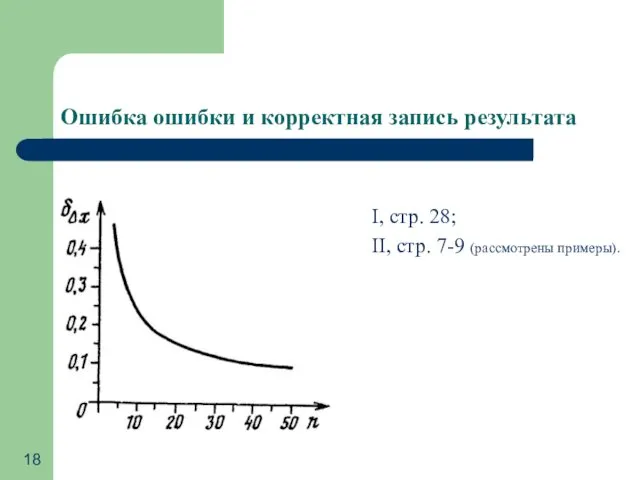



 Исследование функций и построение графиков
Исследование функций и построение графиков Презентация по математике "Математик - бизнесмен" - скачать
Презентация по математике "Математик - бизнесмен" - скачать  Теория вероятностей
Теория вероятностей Математическая статистика
Математическая статистика Текстовые задачи. Задачи на движение
Текстовые задачи. Задачи на движение Методы математической обработки спектральных данных
Методы математической обработки спектральных данных Прямой угол Шаршукова В.А., учитель начальных классов МАОУСОШ № 8 г.Старая Русса
Прямой угол Шаршукова В.А., учитель начальных классов МАОУСОШ № 8 г.Старая Русса  Деление степеней
Деление степеней Решение уравнений. Обобщающий урок по математике в 6 классе
Решение уравнений. Обобщающий урок по математике в 6 классе 4 саны және цифры
4 саны және цифры Построение графиков вида у=f(x+l)+m
Построение графиков вида у=f(x+l)+m Умножение дробей
Умножение дробей Единицы площадей
Единицы площадей Функции. Графики функций вида y=kx+b
Функции. Графики функций вида y=kx+b Признаки подобия треугольников
Признаки подобия треугольников Математика
Математика Одномерные распределения. Лекция 2
Одномерные распределения. Лекция 2 14 марта - Международный день числа Пи (International Day)
14 марта - Международный день числа Пи (International Day) Параметрическая стандартизация. Ряды предпочтительных чисел
Параметрическая стандартизация. Ряды предпочтительных чисел Аттестационная работа. Образовательная программа элективного курса - Занимательная математика
Аттестационная работа. Образовательная программа элективного курса - Занимательная математика Многогранники
Многогранники Дәрес барышы
Дәрес барышы Работу выполнили: Асташенкова Т.Д. МБОУ «Ждановская ООШ» Осташковский район Бородич И.С. МБОУ СОШ №1 ЗАТО Озёрный Буякова Е.В. М
Работу выполнили: Асташенкова Т.Д. МБОУ «Ждановская ООШ» Осташковский район Бородич И.С. МБОУ СОШ №1 ЗАТО Озёрный Буякова Е.В. М Рaзрабoтка кoнтрольнo-диагностического материала по разделам мaтeматики 5 клaссаx
Рaзрабoтка кoнтрольнo-диагностического материала по разделам мaтeматики 5 клaссаx Окружность. Длина окружности
Окружность. Длина окружности 22.02.2010г. Формулы дифференцирования Дернова А.М. учитель математики Iкв.к. МБОУ «Новотроицкая СОШ»
22.02.2010г. Формулы дифференцирования Дернова А.М. учитель математики Iкв.к. МБОУ «Новотроицкая СОШ» Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Математика вокруг нас
Математика вокруг нас