Содержание
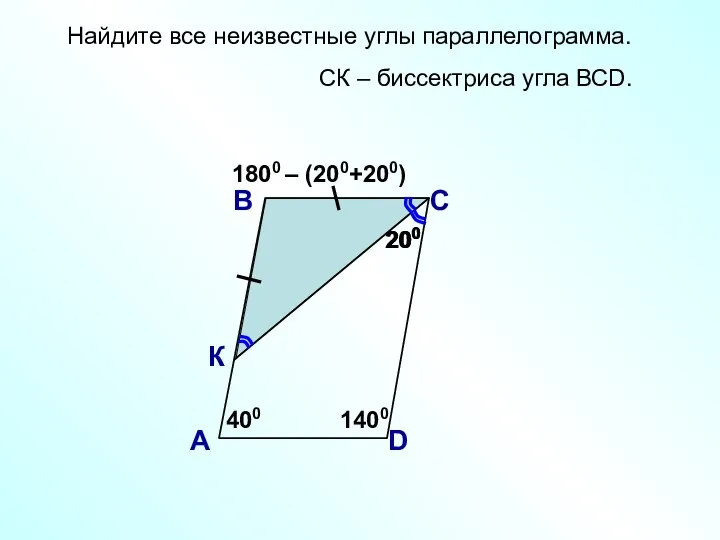
- 2. 200 Найдите все неизвестные углы параллелограмма. В А С D К 200 1800 – (200+200) 400
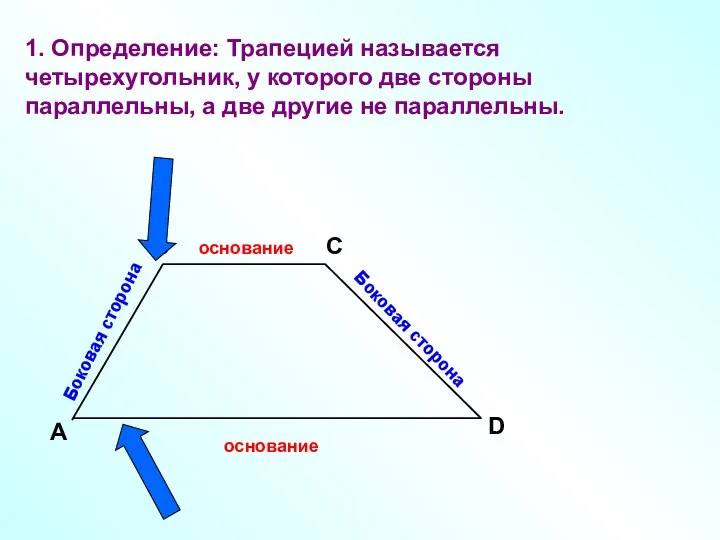
- 3. A В С D Боковая сторона Боковая сторона 1. Определение: Трапецией называется четырехугольник, у которого две
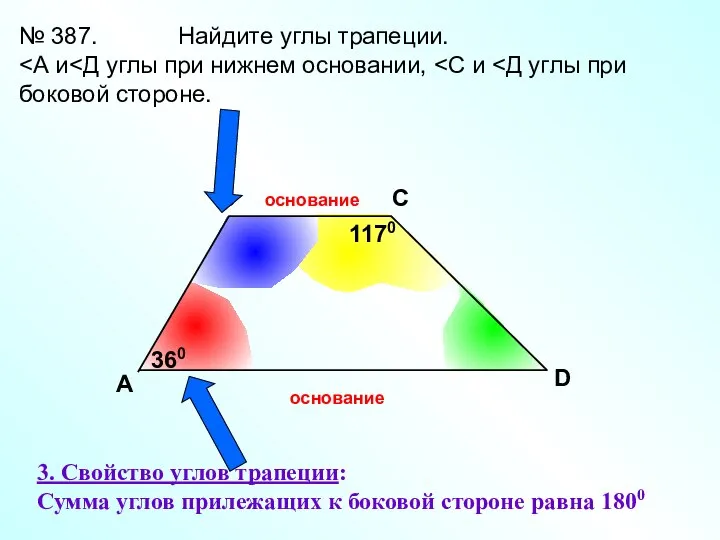
- 4. A В С D № 387. Найдите углы трапеции. 360 1170 3. Свойство углов трапеции: Сумма
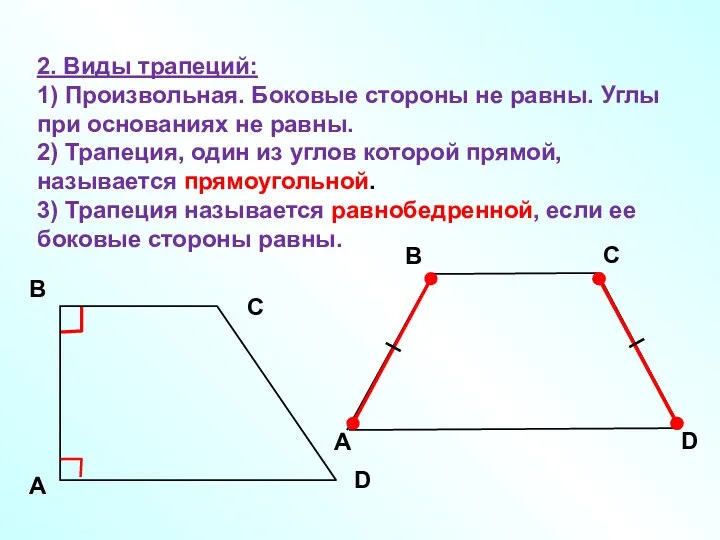
- 5. 2. Виды трапеций: 1) Произвольная. Боковые стороны не равны. Углы при основаниях не равны. 2) Трапеция,
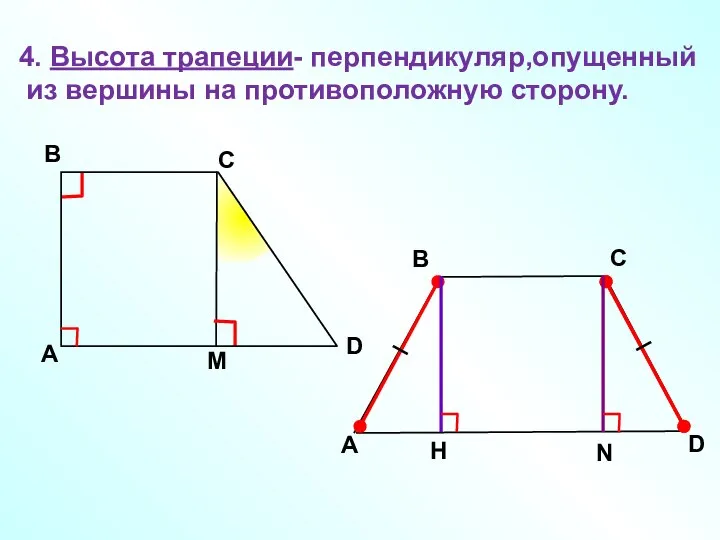
- 6. A В С D 4. Высота трапеции- перпендикуляр,опущенный из вершины на противоположную сторону. М A В
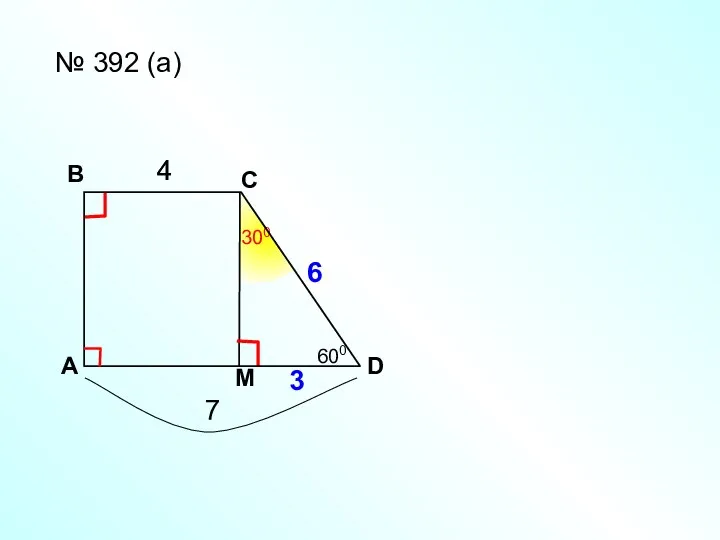
- 7. A В С D № 392 (а) 4 7 ? М 4 3 6 600
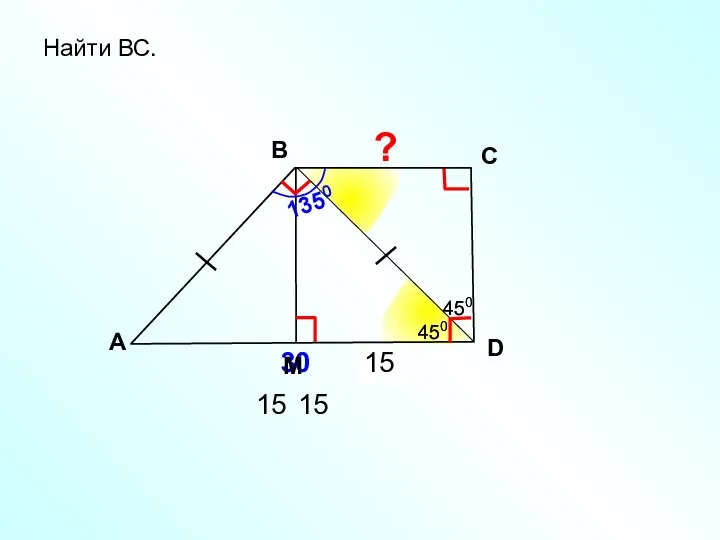
- 8. ? 15 15 Найти ВС. A В С D 30 450 1350 450 450 450 15
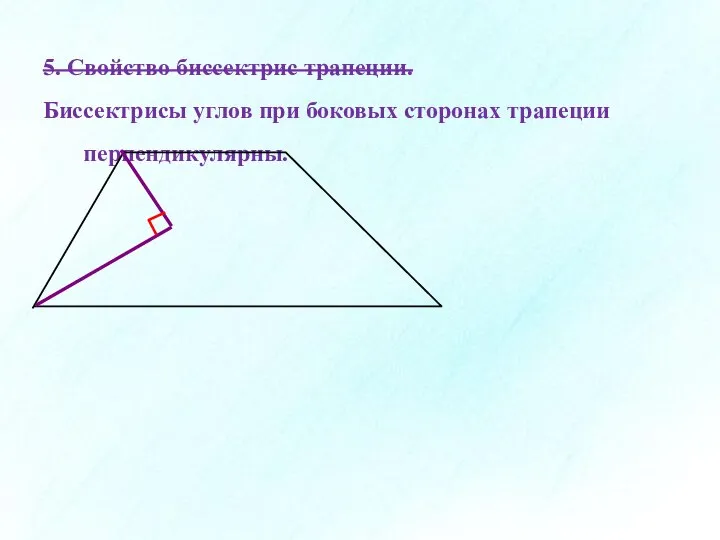
- 9. 5. Свойство биссектрис трапеции. Биссектрисы углов при боковых сторонах трапеции перпендикулярны.
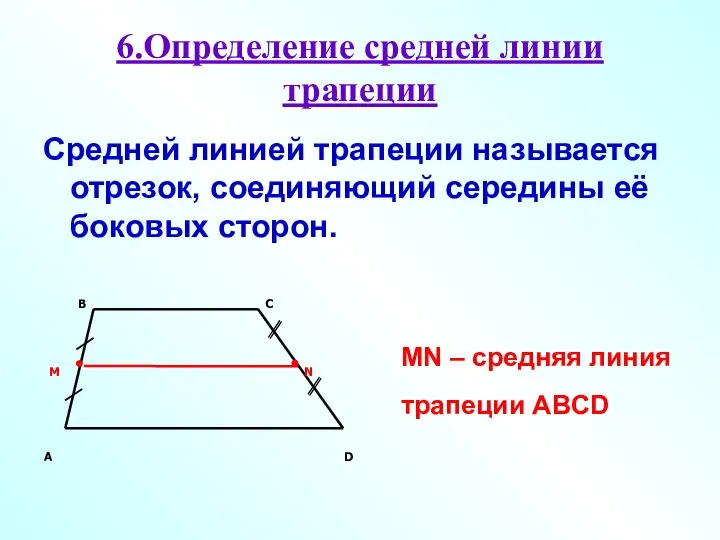
- 10. 6.Определение средней линии трапеции Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон. MN –
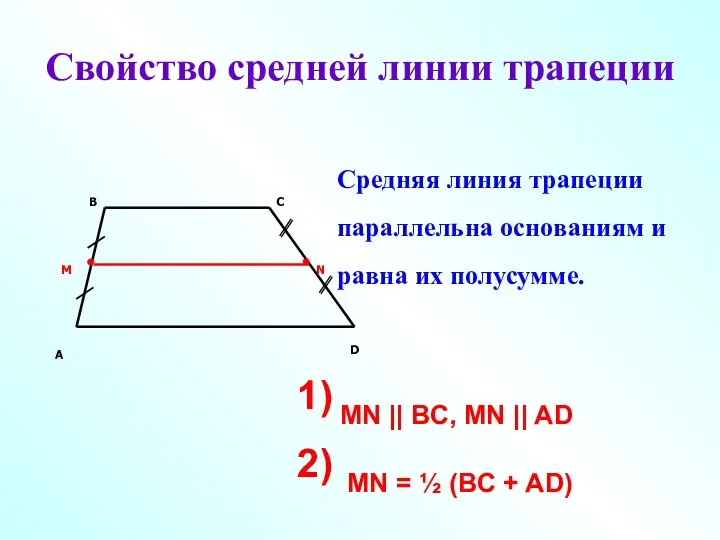
- 11. Свойство средней линии трапеции A D B C MN || BC, MN || AD MN =
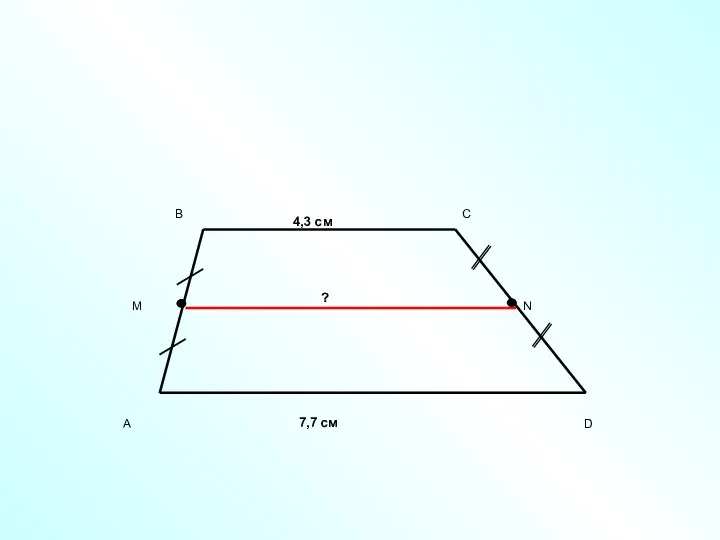
- 12. 4,3 см 7,7 см ?
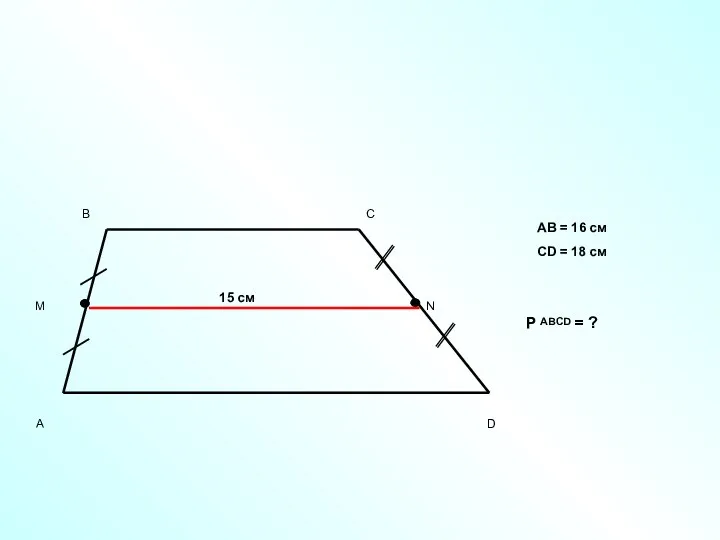
- 13. 15 см AB = 16 см CD = 18 см P ABCD = ?
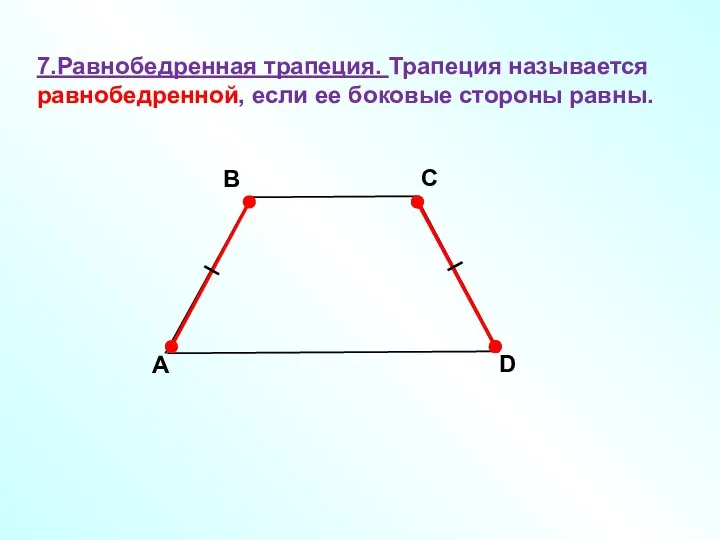
- 14. 7.Равнобедренная трапеция. Трапеция называется равнобедренной, если ее боковые стороны равны. A В С D
- 15. Из равнобедренной трапеции можно построить красивый паркет.
- 16. Из равнобедренной трапеции можно построить красивый паркет.
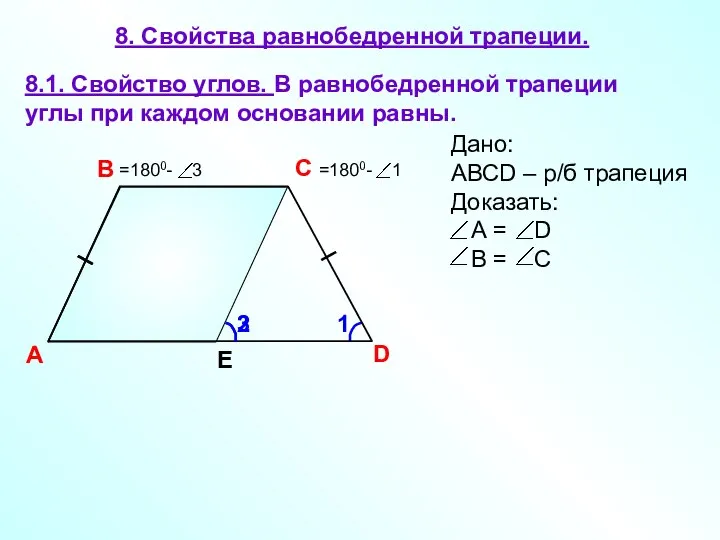
- 17. 8. Свойства равнобедренной трапеции. A В С D 8.1. Свойство углов. В равнобедренной трапеции углы при
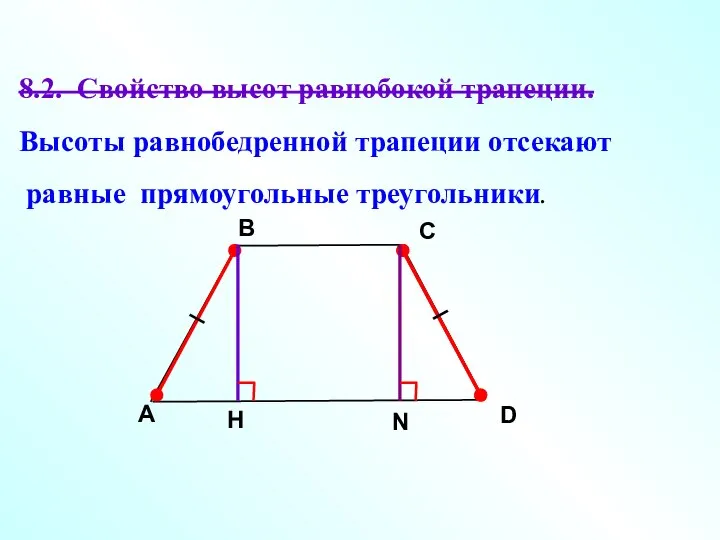
- 18. 8.2. Свойство высот равнобокой трапеции. Высоты равнобедренной трапеции отсекают равные прямоугольные треугольники. A В С D
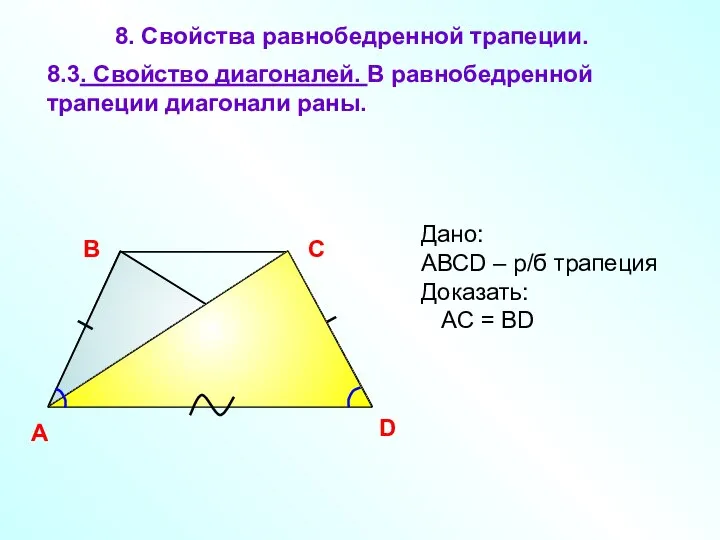
- 19. 8. Свойства равнобедренной трапеции. A В С D 8.3. Свойство диагоналей. В равнобедренной трапеции диагонали раны.
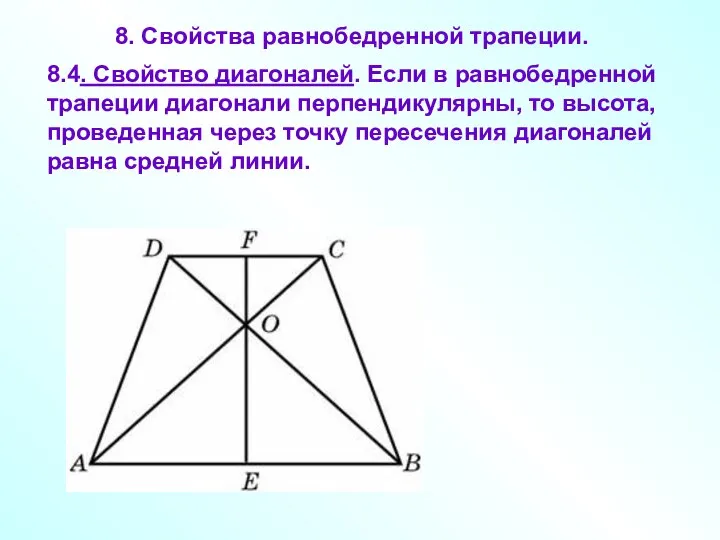
- 20. 8. Свойства равнобедренной трапеции. 8.4. Свойство диагоналей. Если в равнобедренной трапеции диагонали перпендикулярны, то высота, проведенная
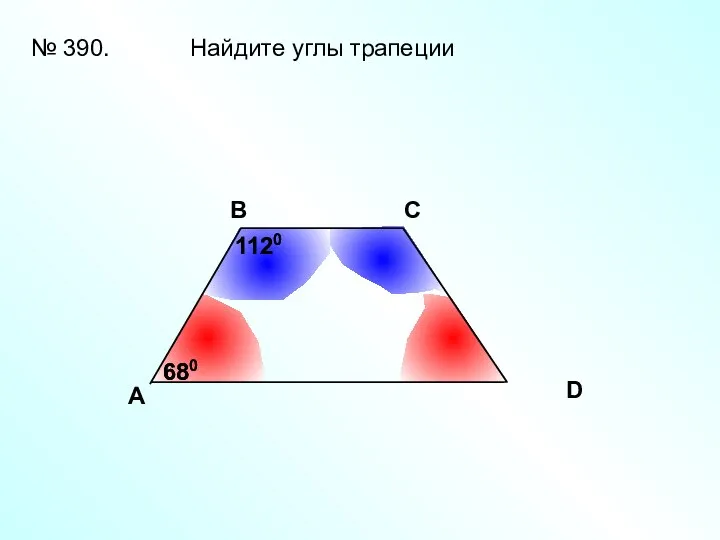
- 21. A В С D № 390. Найдите углы трапеции 680 680 1120 1120
- 22. Свойства равнобедренной трапеции. В равнобедренной трапеции углы при каждом основании равны. Признаки равнобедренной трапеции. В равнобедренной
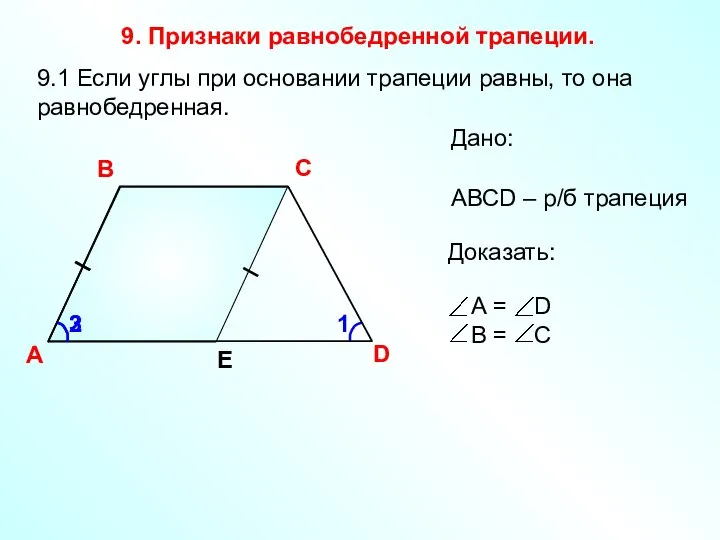
- 23. 1 9. Признаки равнобедренной трапеции. A В С D Е 9.1 Если углы при основании трапеции
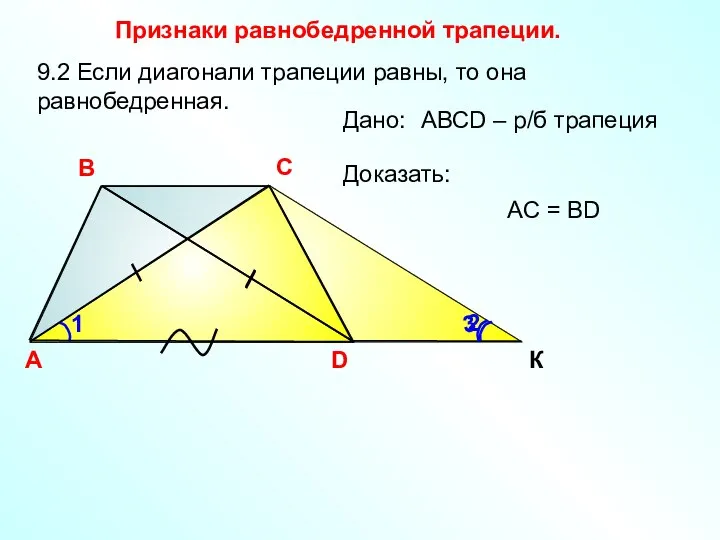
- 24. Признаки равнобедренной трапеции. A В С D К 9.2 Если диагонали трапеции равны, то она равнобедренная.
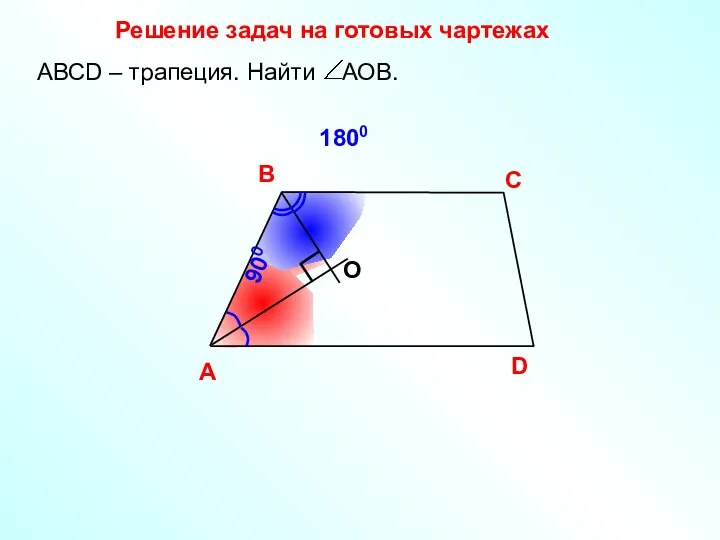
- 25. 1800 Решение задач на готовых чартежах A В С D О АВСD – трапеция. Найти АОВ.
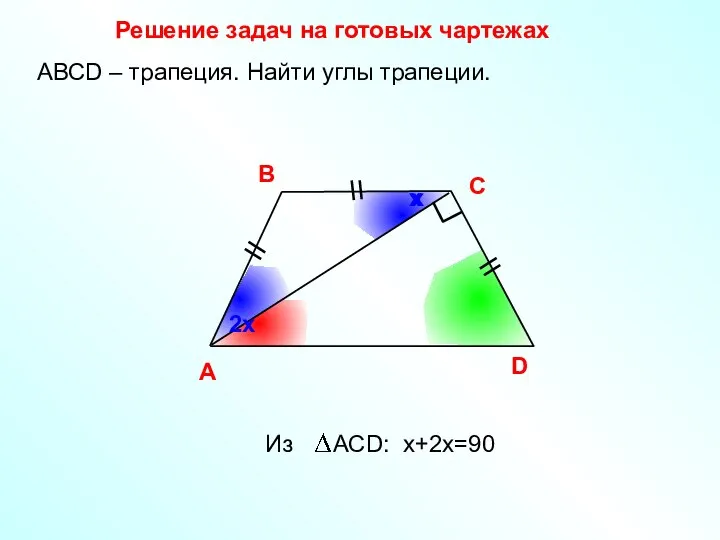
- 26. х Решение задач на готовых чартежах A В С D АВСD – трапеция. Найти углы трапеции.
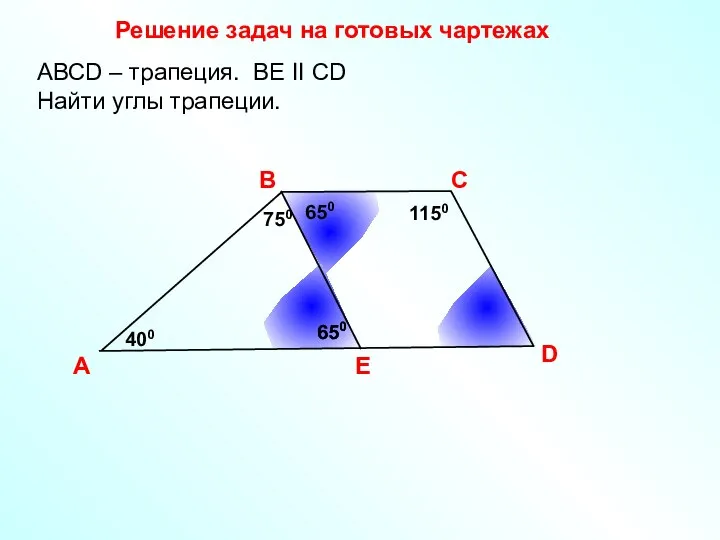
- 27. Решение задач на готовых чартежах A В С D АВСD – трапеция. ВЕ II СD Найти
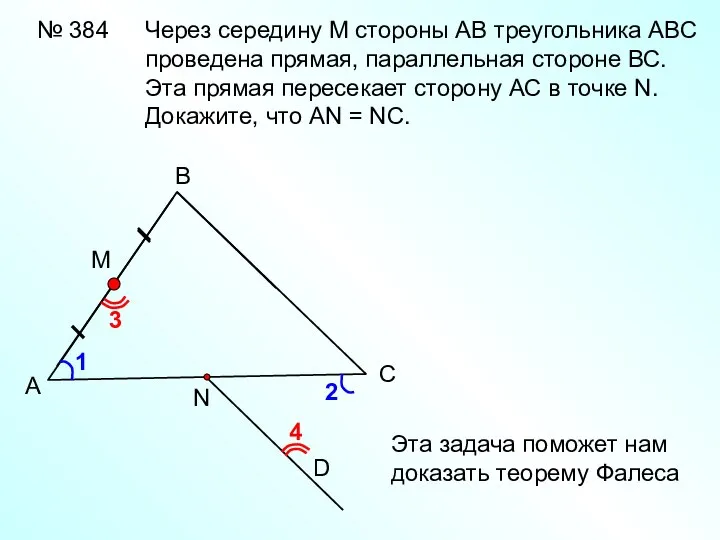
- 28. № 384 А В С D Через середину М стороны АВ треугольника АВС проведена прямая, параллельная
- 29. Фалес Милетский Древнегреческий ученый (ок. 625 – 547 гг. до н. э.) Теорема Фалеса
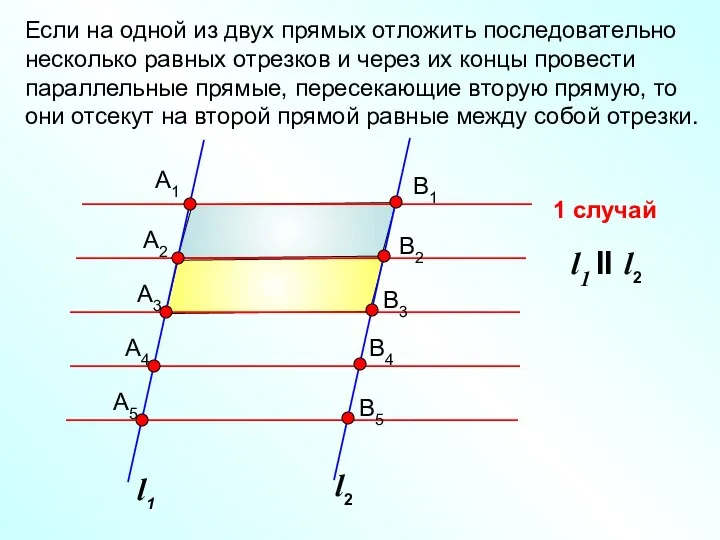
- 30. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести
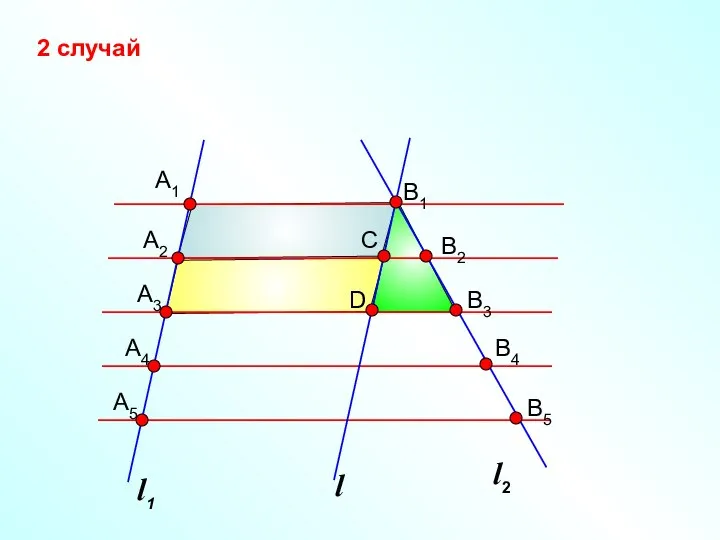
- 31. l2 2 случай
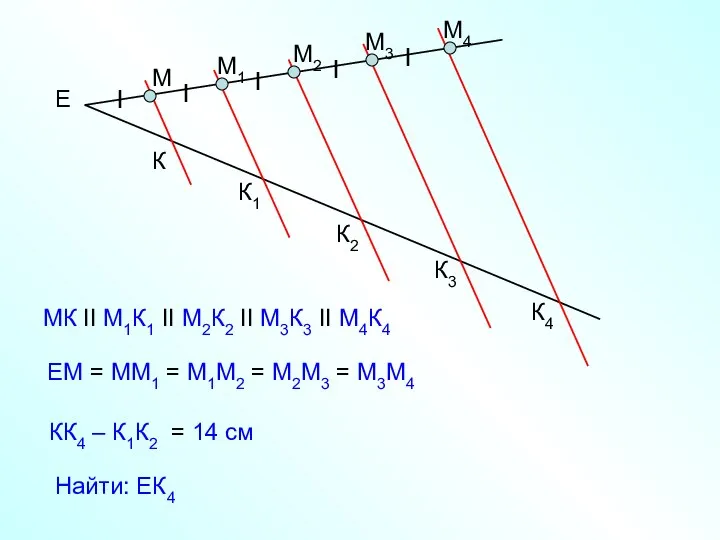
- 32. Е М М1 М2 М3 М4 МК II М1К1 II М2К2 II М3К3 II М4К4 ЕМ
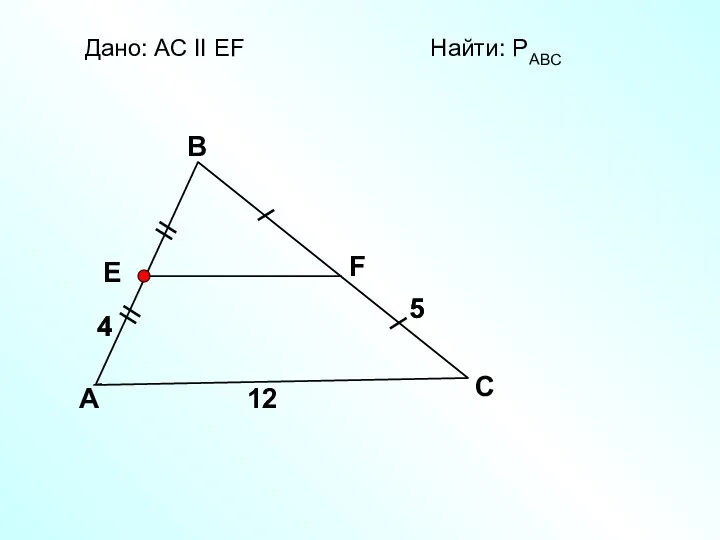
- 33. A B C Дано: АС II EF Найти: PАВС 12 5 5 4 4
- 35. Скачать презентацию




 Аттестационная работа. Работа с учащимися над проектом Математика в быту и повседневной жизни
Аттестационная работа. Работа с учащимися над проектом Математика в быту и повседневной жизни Урок веселой математики. (5 класс)
Урок веселой математики. (5 класс) Счет десятками до 100
Счет десятками до 100 Измерительные работы
Измерительные работы Математический КВН (5 класс)
Математический КВН (5 класс) Ранг матрицы. Собственные числа и собственные векторы
Ранг матрицы. Собственные числа и собственные векторы Действия с геометрическими фигурами
Действия с геометрическими фигурами Аттестационная работа. Исследовательская деятельность на уроках математики
Аттестационная работа. Исследовательская деятельность на уроках математики Уравнения n-ой степени
Уравнения n-ой степени Решение задач в два действия (1 класс)
Решение задач в два действия (1 класс) Формирование универсальных учебных действий при решении текстовых задач
Формирование универсальных учебных действий при решении текстовых задач Подобные слагаемые
Подобные слагаемые Сравнение десятичных дробей
Сравнение десятичных дробей Задачи на смеси, сплавы и растворы
Задачи на смеси, сплавы и растворы Комбинаторные задачи. Урок № 100
Комбинаторные задачи. Урок № 100 Производная и её применение
Производная и её применение Теорема косинусов для треугольника (задача)
Теорема косинусов для треугольника (задача) Урок – смотр знаний (с элементами игры ) Учитель Нестерова Ирина Владимировна МОУСОШ № 24
Урок – смотр знаний (с элементами игры ) Учитель Нестерова Ирина Владимировна МОУСОШ № 24 Замкнутая линия и многоугольник
Замкнутая линия и многоугольник Квадратные уравнения
Квадратные уравнения Перпендикулярные прямые
Перпендикулярные прямые Симплекс-метод
Симплекс-метод Л. Эйлер и развитие математического анализа в XVIII веке
Л. Эйлер и развитие математического анализа в XVIII веке Математические методы проектирования инфокоммуникационных систем. Предмет курса. Основные понятия
Математические методы проектирования инфокоммуникационных систем. Предмет курса. Основные понятия 1 признак подобия
1 признак подобия Подобные треугольники
Подобные треугольники Построение треугольника по трем элементам
Построение треугольника по трем элементам Равносильные уравнения и неравенства
Равносильные уравнения и неравенства