Содержание
- 2. Оглавление §1. Треугольники а) Треугольники б) Равные треугольники в) Первый признак равенства треугольников §2. Медианы, биссектрисы
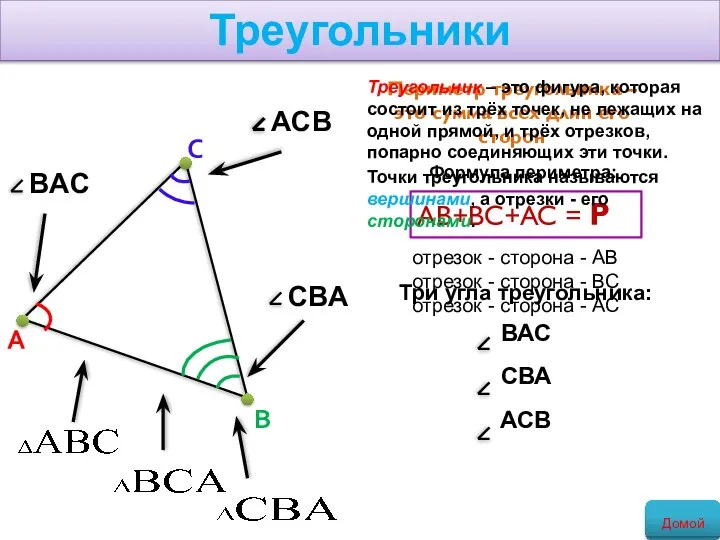
- 3. Периметр треугольника – это сумма всех длин его сторон AB+BC+AC = P Формула периметра: Треугольник –
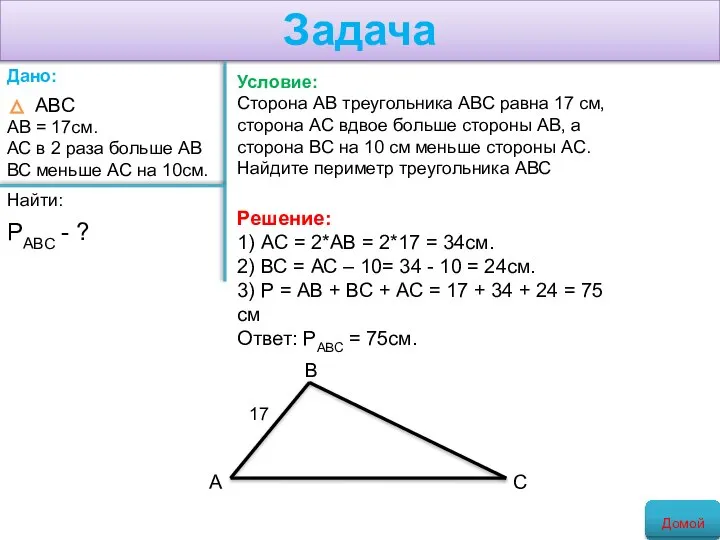
- 4. Задача Условие: Сторона АВ треугольника АВС равна 17 см, сторона АС вдвое больше стороны АВ, а
- 5. Треугольники
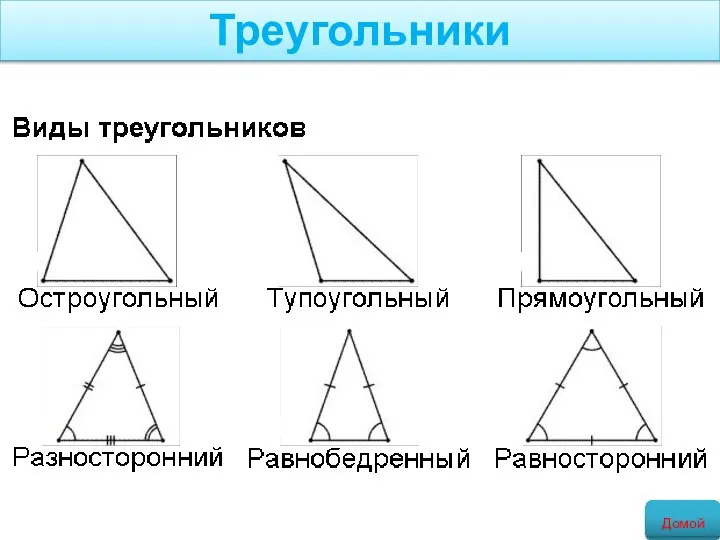
- 6. Треугольники Остроугольный треугольник – это такой треугольник, у которого все углы острые ( Тупоугольный треугольный –
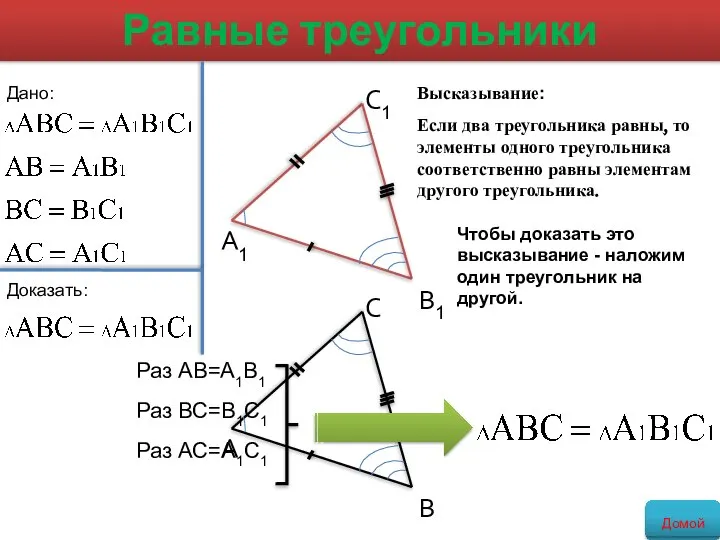
- 7. Высказывание: Если два треугольника равны, то элементы одного треугольника соответственно равны элементам другого треугольника. Равные треугольники
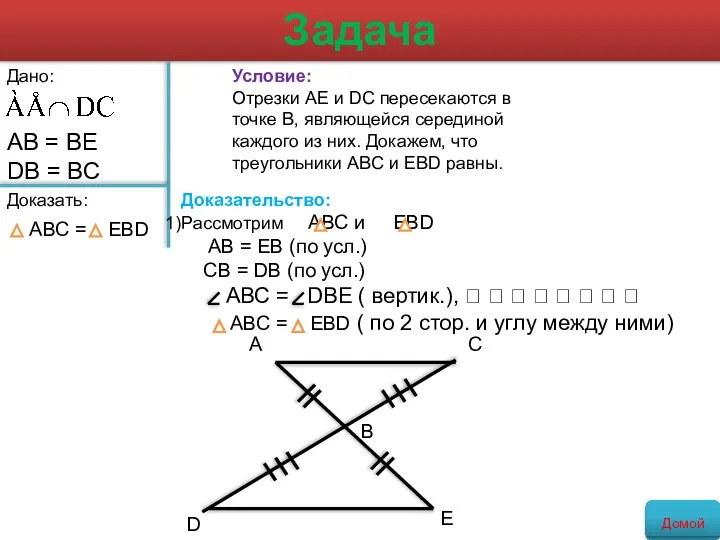
- 8. Задача Условие: Отрезки АЕ и DC пересекаются в точке В, являющейся серединой каждого из них. Докажем,
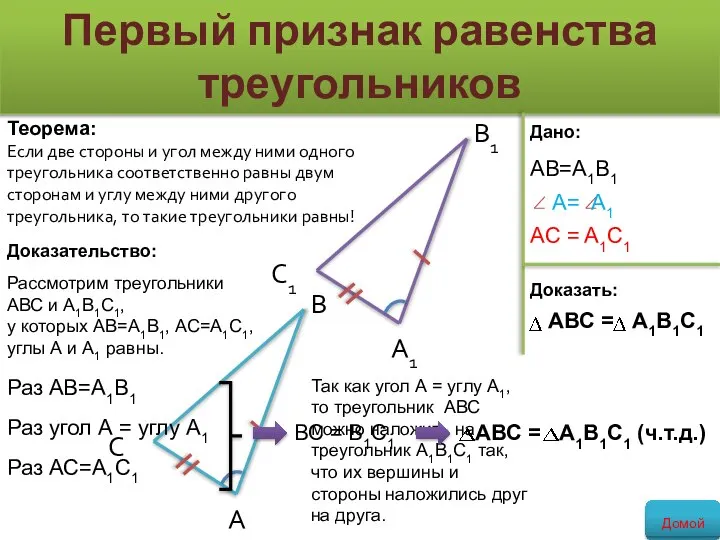
- 9. Теорема: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу
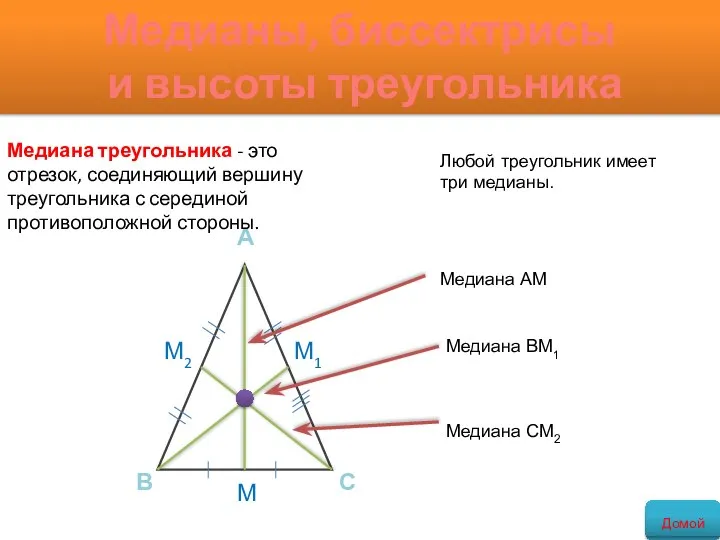
- 10. Медианы, биссектрисы и высоты треугольника Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной
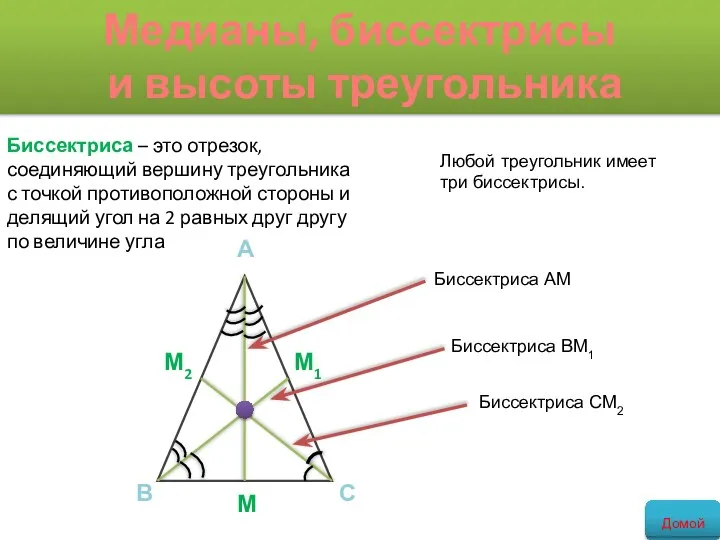
- 11. Медианы, биссектрисы и высоты треугольника Биссектриса – это отрезок, соединяющий вершину треугольника с точкой противоположной стороны
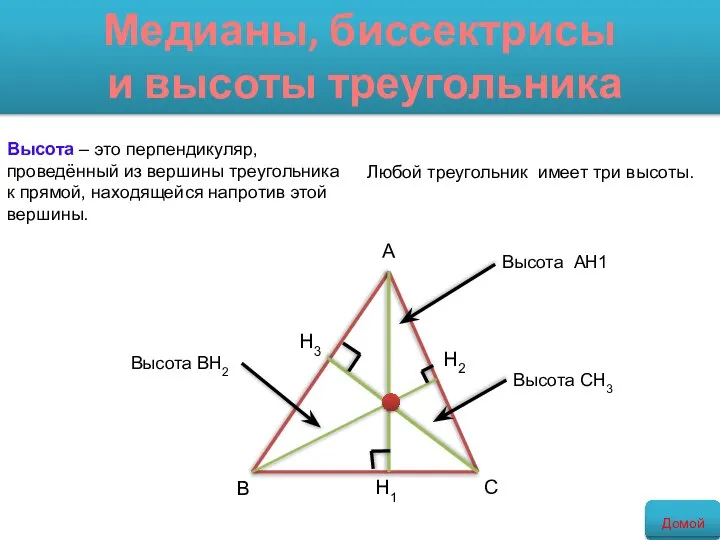
- 12. Высота – это перпендикуляр, проведённый из вершины треугольника к прямой, находящейся напротив этой вершины. Любой треугольник
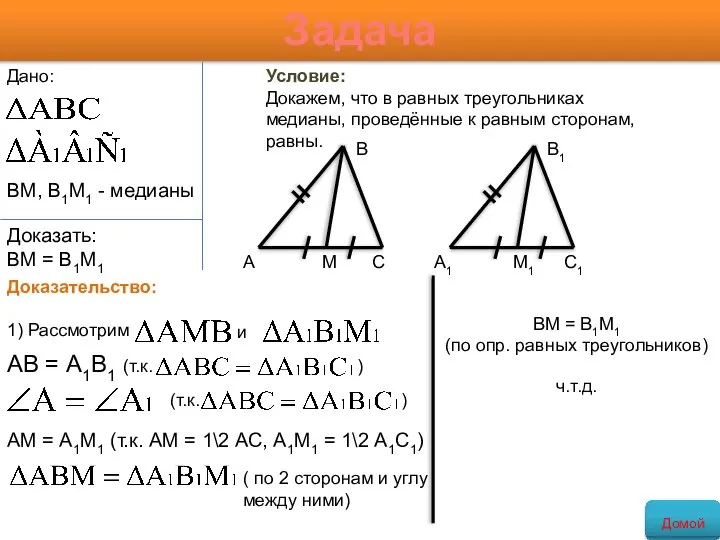
- 13. Задача Условие: Докажем, что в равных треугольниках медианы, проведённые к равным сторонам, равны. ВМ = В1М1
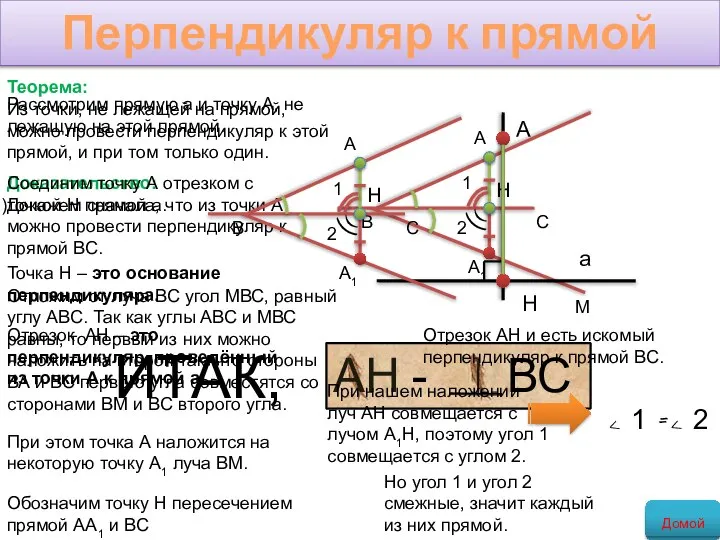
- 14. Перпендикуляр к прямой Теорема: Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой,
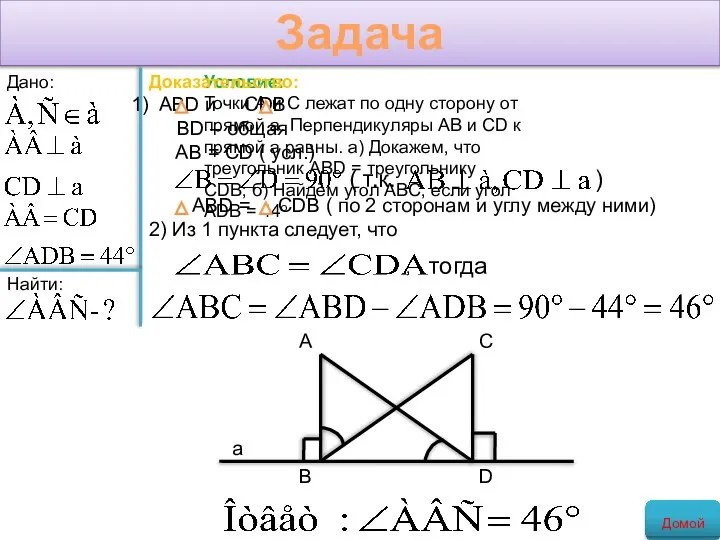
- 15. Задача Условие: Точки А и С лежат по одну сторону от прямой а. Перпендикуляры АВ и
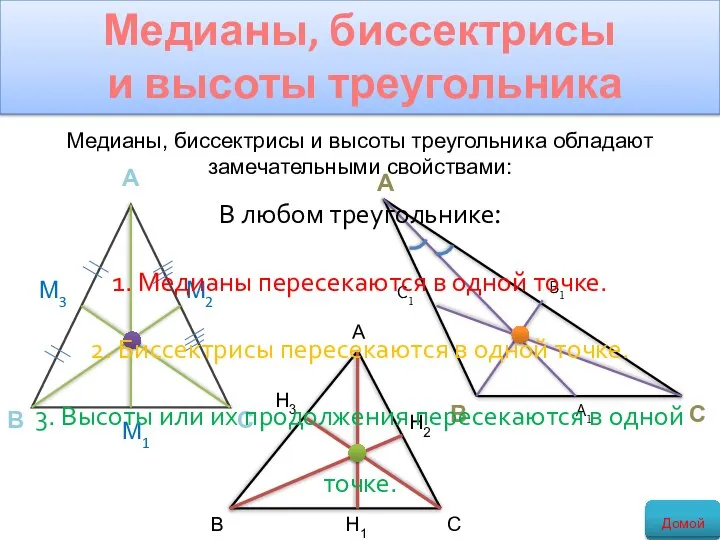
- 16. Медианы, биссектрисы и высоты треугольника В любом треугольнике: 1. Медианы пересекаются в одной точке. 2. Биссектрисы
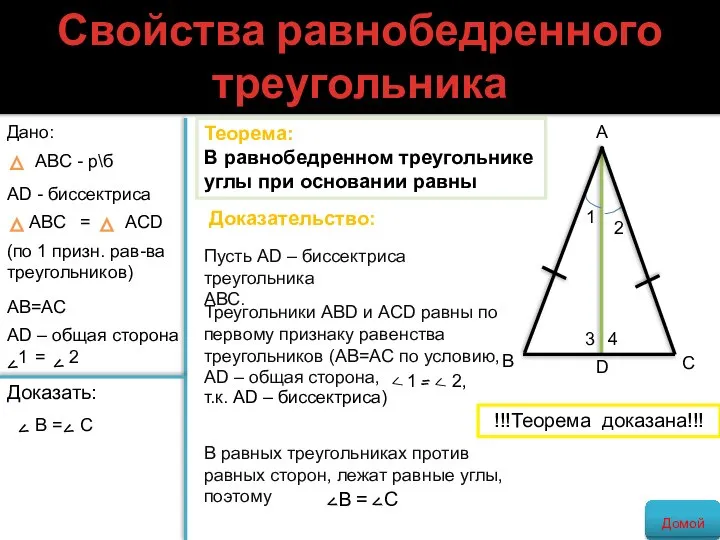
- 17. Свойства равнобедренного треугольника Теорема: В равнобедренном треугольнике углы при основании равны Дано: ABC - р\б AD
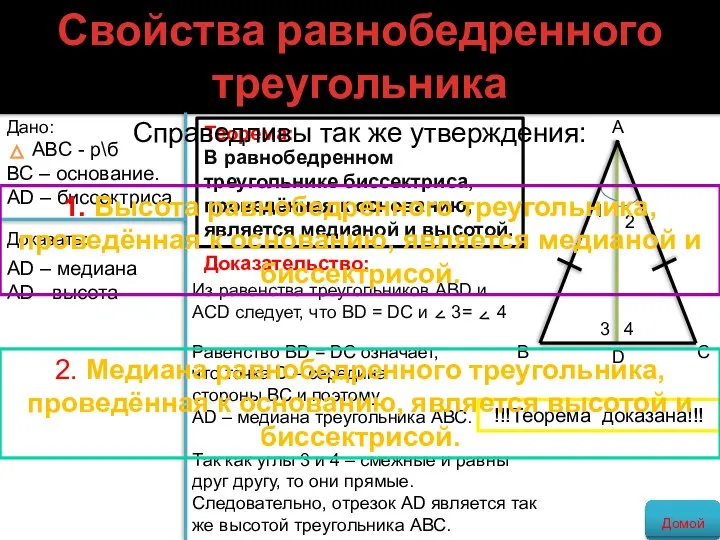
- 18. Свойства равнобедренного треугольника Теорема: В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой. Доказательство:
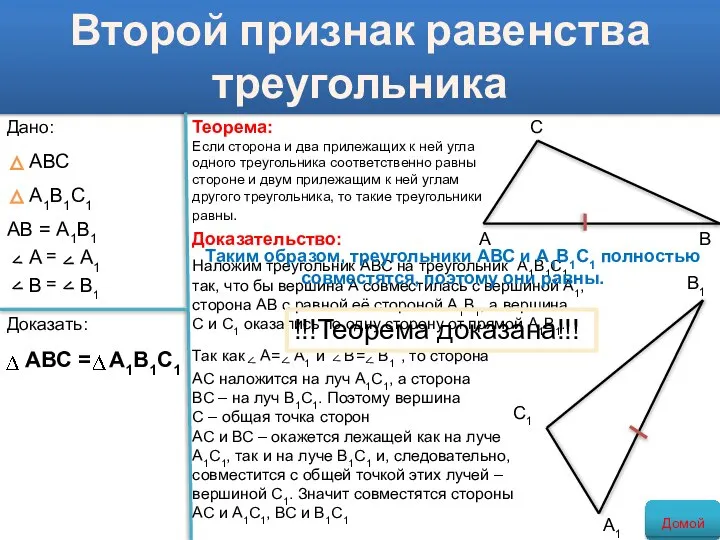
- 19. Второй признак равенства треугольника Теорема: Если сторона и два прилежащих к ней угла одного треугольника соответственно
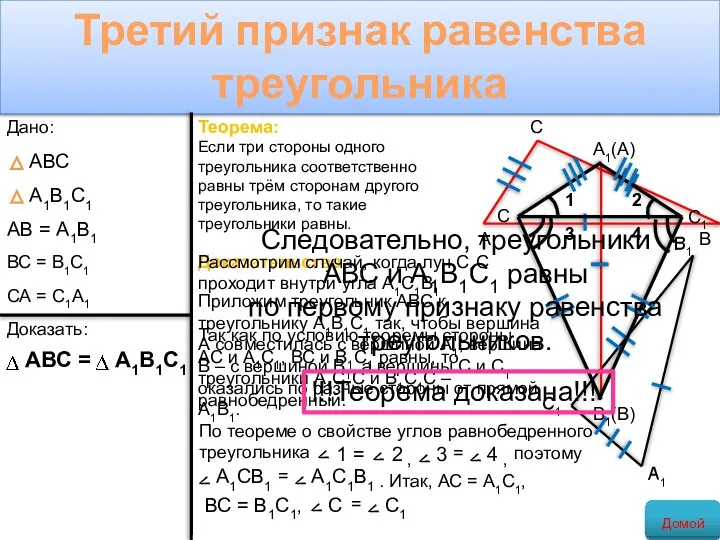
- 20. Третий признак равенства треугольника Теорема: Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника,
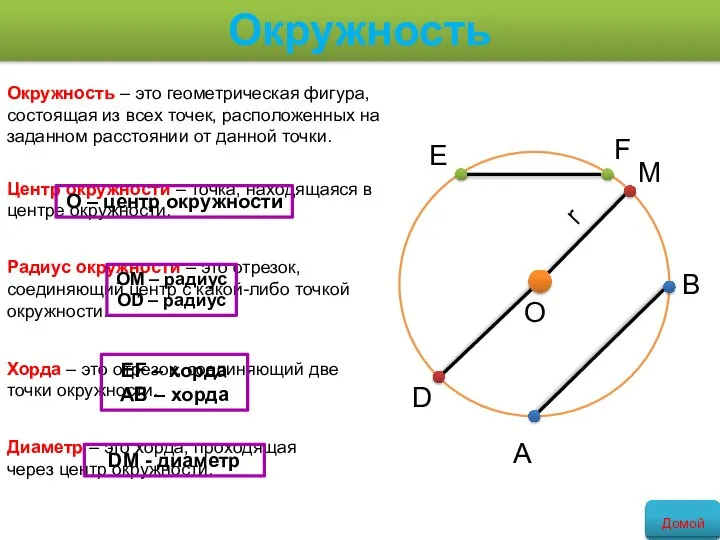
- 21. Окружность Окружность – это геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной
- 23. Скачать презентацию

 Математика 2 класс Тема: Умножение. Цель: познакомить с новым действием, раскрыть смысл действия умножен
Математика 2 класс Тема: Умножение. Цель: познакомить с новым действием, раскрыть смысл действия умножен Площадь параллелограмма
Площадь параллелограмма Деление числа в данном отношении
Деление числа в данном отношении Презентация на тему Математические загадки и ребусы
Презентация на тему Математические загадки и ребусы  Решение задач
Решение задач Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей Устные упражнения. Определение производной. (10 класс)
Устные упражнения. Определение производной. (10 класс) Числовые функции
Числовые функции Укажите только ответы к следующим уравнениям
Укажите только ответы к следующим уравнениям  The Chain Rule
The Chain Rule Плоскость. Уравнения плоскости
Плоскость. Уравнения плоскости Аттестационная работа. Образовательная программа курса внеурочной деятельности для 6-х классов «Занимательная математика»
Аттестационная работа. Образовательная программа курса внеурочной деятельности для 6-х классов «Занимательная математика» Современные технологии на уроке математики
Современные технологии на уроке математики Правильная пирамида
Правильная пирамида Делимость чисел
Делимость чисел Веселый математический тест
Веселый математический тест Презентация по математике "Всегда ли 2 × 2 четыре?" - скачать
Презентация по математике "Всегда ли 2 × 2 четыре?" - скачать  Статистический анализ результатов мониторинга
Статистический анализ результатов мониторинга Теорема Пифагора
Теорема Пифагора Вычитание чисел 5,6,7,8,9. Уменьшаемое, вычитаемое, разность
Вычитание чисел 5,6,7,8,9. Уменьшаемое, вычитаемое, разность Огюстен Луи Коши
Огюстен Луи Коши Старинные меры длины Выполнила ученица 5 А класса МОУ «СОШ № 1 р.п. Новые Бурасы Новобурасского района Саратовской области Суслов
Старинные меры длины Выполнила ученица 5 А класса МОУ «СОШ № 1 р.п. Новые Бурасы Новобурасского района Саратовской области Суслов Способы нахождения наибольшего общего делителя и наименьшего общего кратного натуральных чисел
Способы нахождения наибольшего общего делителя и наименьшего общего кратного натуральных чисел Методическое портфолио учителя математики
Методическое портфолио учителя математики Письменные приемы сложения и вычитания. Закрепление
Письменные приемы сложения и вычитания. Закрепление Сумма углов треугольника
Сумма углов треугольника Приложения производной. (Тема 4)
Приложения производной. (Тема 4) Вычисление квадратного корня числа. Задания
Вычисление квадратного корня числа. Задания