Содержание
- 2. Схема вычисления определителя второго порядка (произведение элементов главной диагонали минус произведение элементов побочной диагонали). Пример. Вычислить
- 3. Определителем третьего порядка называется число, обозначаемое и равное Вычислительная математика .
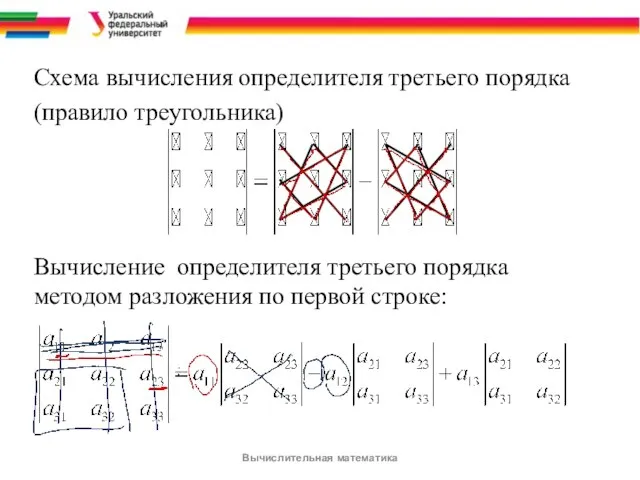
- 4. Схема вычисления определителя третьего порядка (правило треугольника) Вычисление определителя третьего порядка методом разложения по первой строке:
- 5. Пример. Вычислить определитель двумя способами Вычислительная математика
- 6. §2. Вектор. Линейные операции над векторами. Вектор – множество направленных отрезков, имеющих общее направление и одинаковую
- 7. Вектор, длина которого равна 0, называется нулевым, обозначают (у такого вектора совпадают начальная и конечная точки).
- 8. Вектор называется противоположным вектору Два вектора называются коллинеарными, если они лежат на одной прямой или на
- 9. Два вектора равны, если они сонаправлены и имеют одинаковую длину: Три вектора в пространстве называются компланарными,
- 10. Линейные операции над векторами: ‑ сложение векторов; ‑ вычитание векторов; ‑ умножение вектора на число. Вычислительная
- 11. §3. Базис. Координаты вектора в базисе Базис на плоскости – это упорядоченная пара неколлинеарных векторов Если
- 12. Пусть ‑ произвольный вектор на плоскости. От произвольной точки О отложим векторы, равные и Следовательно существуют
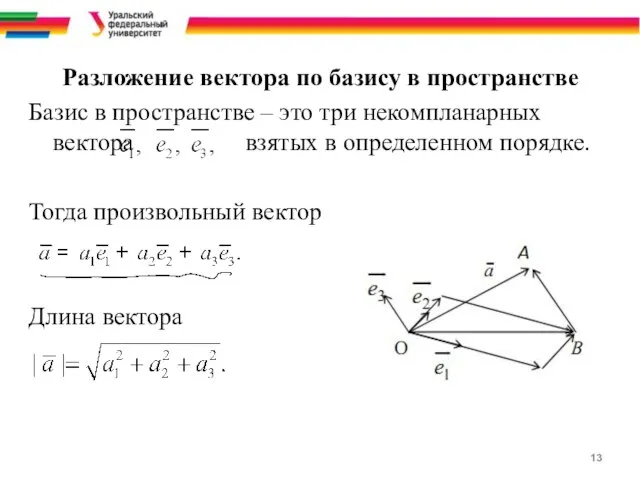
- 13. Разложение вектора по базису в пространстве Базис в пространстве – это три некомпланарных вектора взятых в
- 14. Значения называются направляющими косинусами вектора , причем Направляющие косинусы совпадают с координатами орта
- 15. Свойства координат вектора: 1) при умножении вектора на число его координаты умножаются на это же число;
- 16. Координаты точки. Их связь с координатами вектора Рассмотрим точку А. Вектор называют радиус-вектором точки А, а
- 17. §4. Скалярное произведение векторов Скалярным произведением векторов и называется число, равное произведению длин этих векторов на
- 18. Свойства скалярного произведения: 1) скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти
- 19. Пример. Вычислить если
- 20. Вычисление скалярного произведения в ортонормированном базисе Рассмотрим ортонормированный базис Пусть Тогда
- 22. Пример 1. Найти длину вектора если Вычислительная математика
- 23. Пример 2. Найти вектор коллинеарный вектору если его проекция на вектор равна Вычислительная математика
- 24. §5. Векторное произведение векторов Понятие правой и левой тройки векторов Упорядоченная тройка некомпланарных векторов называется правой,
- 25. Векторным произведением двух векторов и называется такой вектор , длина и направление которого определяются следующими условиями:
- 26. Свойства векторного произведения: 1. (антикоммутативность); 2. 3. (условие коллинеарности двух векторов).
- 27. Вычисление векторного произведения в ортонормированном базисе Пусть Тогда
- 28. Пример. Вычислить
- 30. Пример 1. Вычислить площадь параллелограмма ABCD, если - единичные векторы и
- 31. Пример 2. Найти вектор ортогональный векторам , если и вектор образует тупой угол с осью Oz.
- 32. §6. Смешанное произведение векторов Пусть вектор векторно умножается на вектор затем получившийся вектор скалярно умножается на
- 35. Тогда
- 36. Пример. Вычислить смешанное произведение векторов
- 37. Применения смешанного произведения 1. Проверка компланарности трех векторов: компланарны 2. Проверка принадлежности четырех точек A, B,
- 39. Скачать презентацию


































 Различные способы решения тригонометрических неравенств
Различные способы решения тригонометрических неравенств Решение показательных уравнений и неравенств
Решение показательных уравнений и неравенств Лозунговый шифр
Лозунговый шифр Решение задач. Подготовка к ЕГЭ
Решение задач. Подготовка к ЕГЭ Кластерный анализ
Кластерный анализ Аттестационная работа. Проектная работа «Культура устного счета в изучении математики в России»
Аттестационная работа. Проектная работа «Культура устного счета в изучении математики в России»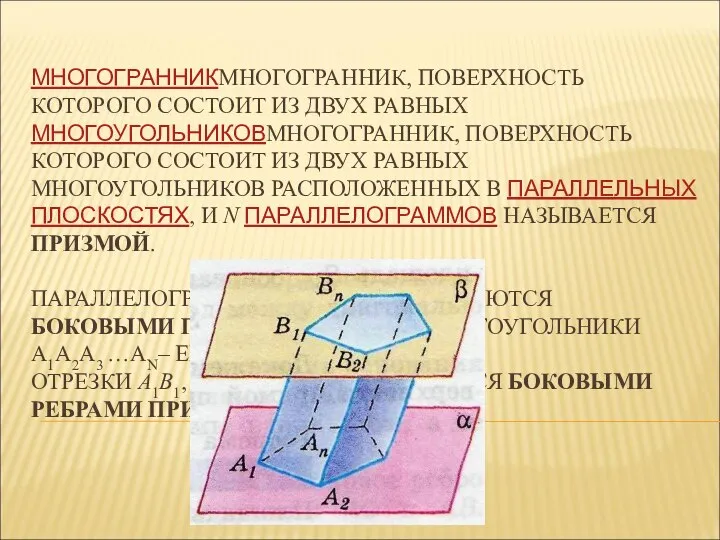 Призма. Виды призмы. Свойства призмы
Призма. Виды призмы. Свойства призмы Лекция 3.1. Криволинейные интегралы. Определение криволинейных интегралов
Лекция 3.1. Криволинейные интегралы. Определение криволинейных интегралов Математический калейдоскоп: www.themegallery.com
Математический калейдоскоп: www.themegallery.com Презентация по математике "Решение задач" - скачать бесплатно
Презентация по математике "Решение задач" - скачать бесплатно Округление натуральных чисел
Округление натуральных чисел Новые типы обратных связей в системах автоматического управления
Новые типы обратных связей в системах автоматического управления 5 класс.
5 класс.  Генеральная совокупность и выборка
Генеральная совокупность и выборка Интерактивная дидактическая игра «Состав чисел до 10». Математика, 1 класс
Интерактивная дидактическая игра «Состав чисел до 10». Математика, 1 класс Отношение. Пропорция
Отношение. Пропорция Виды графиков линейной функции
Виды графиков линейной функции Методы оптимизации объектов
Методы оптимизации объектов Ребусы по математике
Ребусы по математике Математические отношения
Математические отношения Построение графика функции
Построение графика функции Решение уравнений и неравенств, содержащих переменную под знаком модуля
Решение уравнений и неравенств, содержащих переменную под знаком модуля Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Теорема о трёх перпендикулярах
Теорема о трёх перпендикулярах Исчисление предикатов
Исчисление предикатов Аттестационная работа. Решение сложных задач по математике
Аттестационная работа. Решение сложных задач по математике Числовые и алгебраические выражения
Числовые и алгебраические выражения Роль диагностики в обучении математи
Роль диагностики в обучении математи