Содержание
- 2. Комбинаторика. «комбинаторика» происходит от латинского слова combinare – «соединять, сочетать». Определение. Комбинаторика – это раздел математики,
- 3. Пример 2. Сколько трёхзначных чисел можно составить из цифр 1, 3, 5, 7, используя в записи
- 4. Квадратные числа
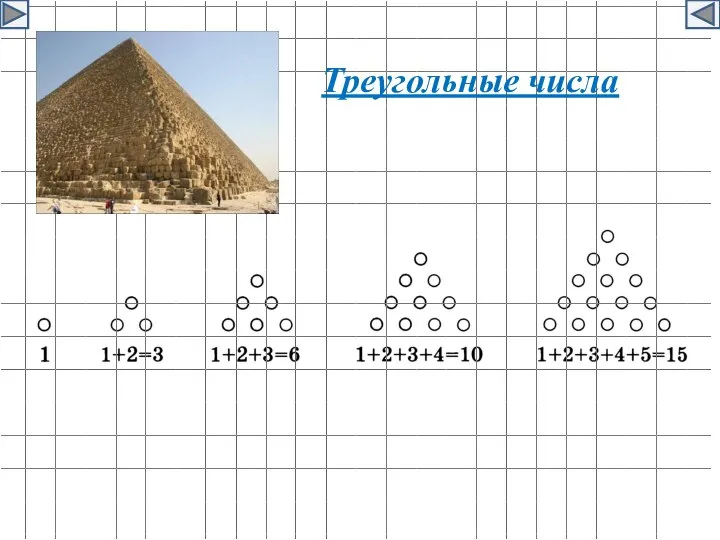
- 5. Треугольные числа
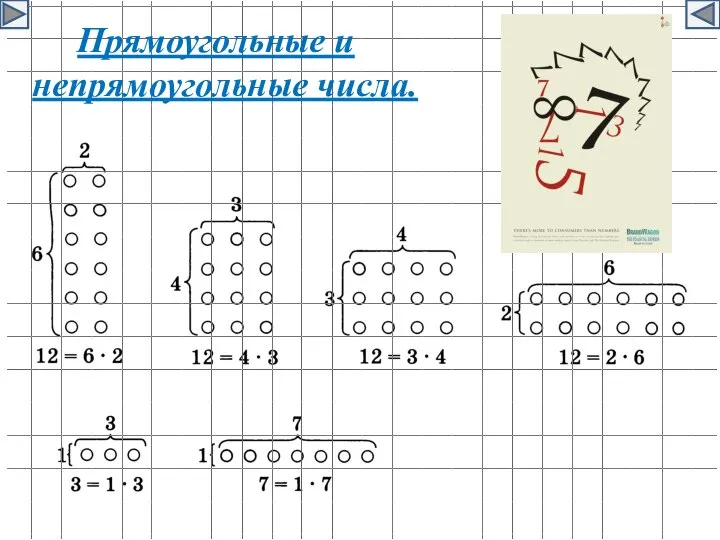
- 6. Прямоугольные и непрямоугольные числа.
- 7. Факториал. Таблица факториалов: Определение. Факториалом натурального числа n называется произведение всех натуральных чисел от 1 до
- 8. Перестановки. Определение. Перестановкой называется конечное множество, в котором установлен порядок элементов. Число всевозможных перестановок из n
- 9. Пример 1. Сколькими способами могут быть расставлены восемь участниц финального забега на восьми беговых дорожках? Решение:
- 10. Пример 2. Сколько различных четырёхзначных чисел можно составить из цифр 0, 1, 2, 3, причём в
- 11. Пример 3. Имеется 10 различных книг, среди которых есть трёхтомник одного автора. Сколькими способами можно расставить
- 12. Размещения. Определение. Размещением из n элементов , называют конечного множества по k, где упорядоченное множество, состоящее
- 13. Пример 1. Из 12 учащихся нужно отобрать по одному человеку для участия в городских олимпиадах по
- 14. Пример 2. Сколько существует семизначных телефонных номеров, в которых все цифры различны и первая цифра отлична
- 15. Пример 3. Сколько существует трёхзначных чисел, составленных из цифр 1, 2, 3, 4, 5, 6 (без
- 16. Сочетания. Определение. Подмножества, составленные из n элементов данного множества и содержащие k элементов в каждом подмножестве,
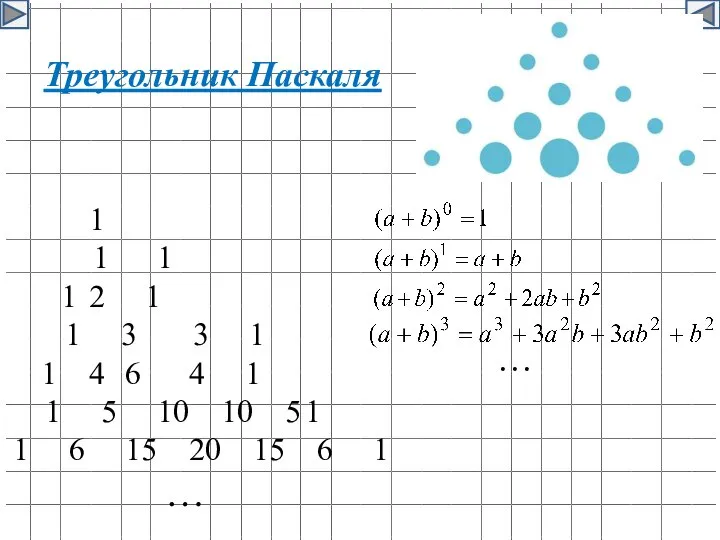
- 17. Треугольник Паскаля 1 1 1 1 2 1 1 3 3 1 1 4 6 4
- 18. Треугольник Паскаля
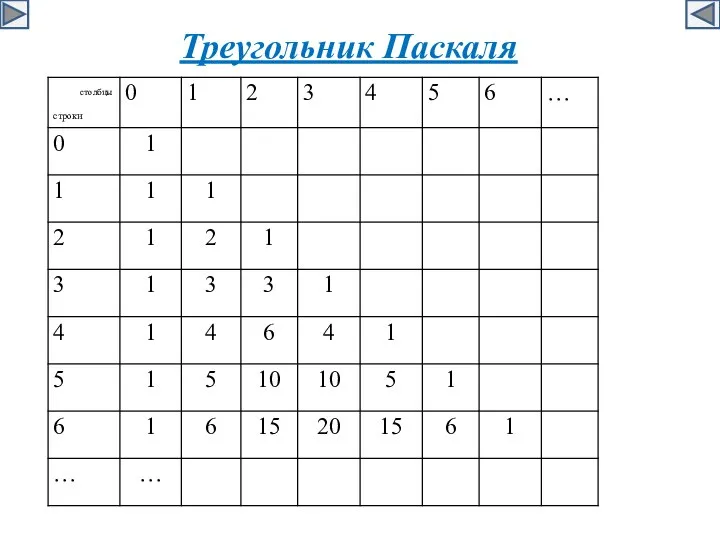
- 19. Треугольник Паскаля …
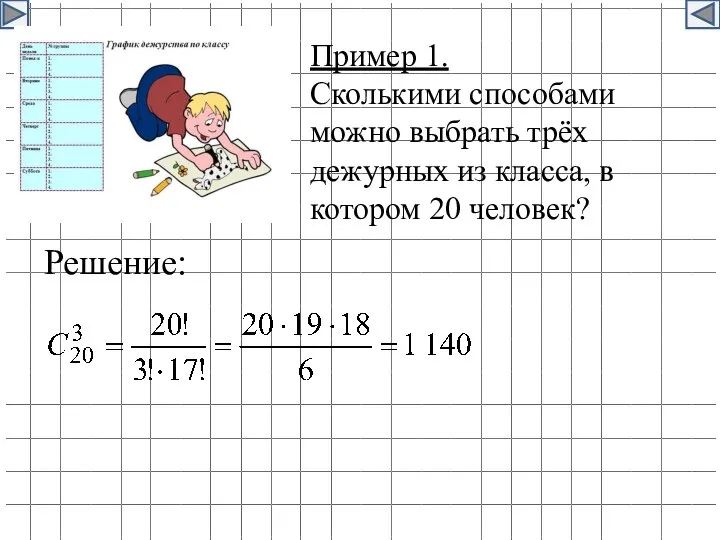
- 20. Пример 1. Сколькими способами можно выбрать трёх дежурных из класса, в котором 20 человек? Решение:
- 21. Пример 2. Из вазы с цветами, в которой стоят 10 красных гвоздик и 5 белых, выбирают
- 22. Пример 3. Семь огурцов и три помидора надо положить в два пакета так, чтобы в каждом
- 23. Частота и вероятность. Определение. Частотой случайного события в серии испытаний называется отношение числа испытаний, в которых
- 24. Частота и вероятность. Определение. Вероятностью события А называется отношение числа благоприятных для А исходов к числу
- 25. Пример 1. В урне 10 одинаковых шаров разного цвета: 2 красных, 3 синих, 5 жёлтых. Шары
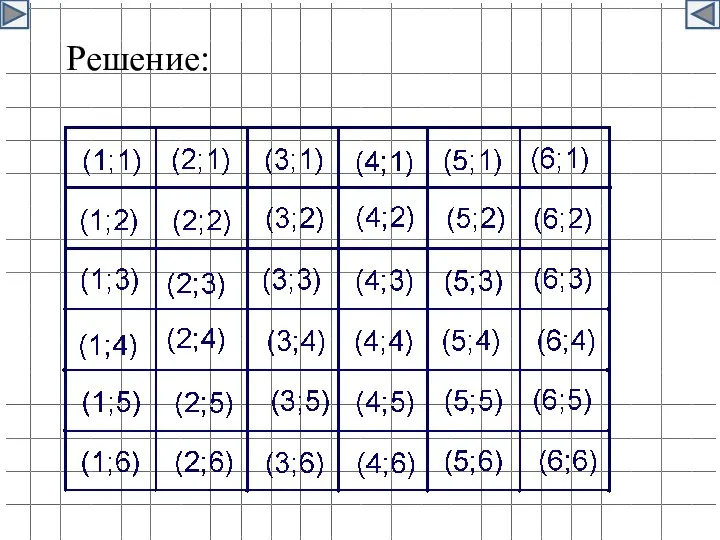
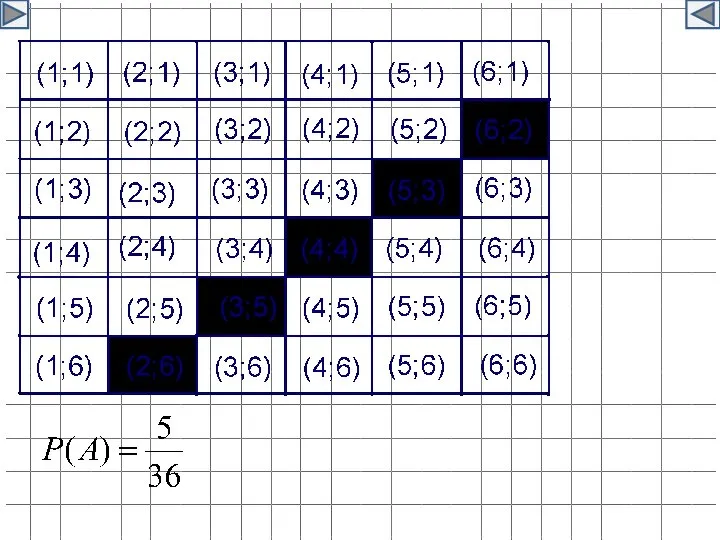
- 26. Пример 2. Коля и Миша бросают два игральных кубика. Они договорились, что если при бросании кубиков
- 27. Решение:
- 30. Пример 3. Из собранных 10 велосипедов только 7 не имеют дефектов. Какова вероятность того, что 4
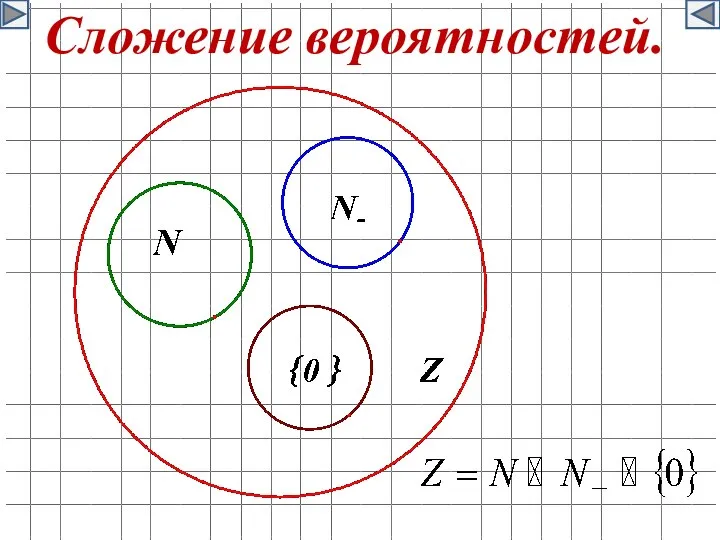
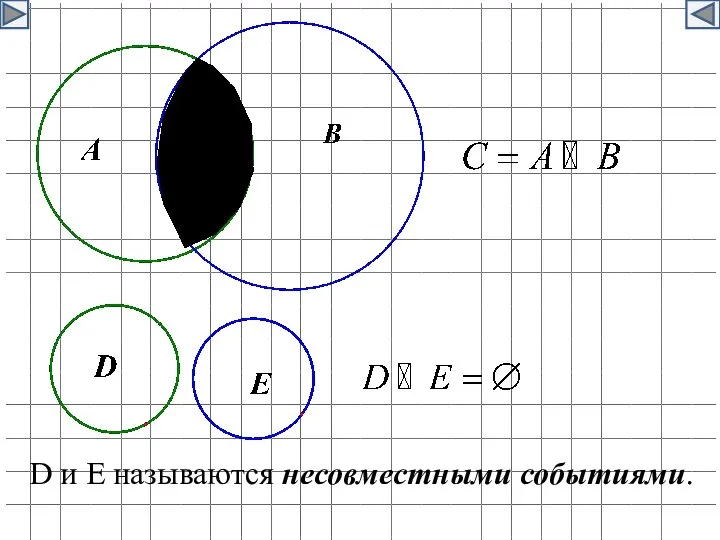
- 31. Сложение вероятностей.
- 32. D и E называются несовместными событиями.
- 33. Сложение вероятностей. Вероятность наступления хотя бы одного из двух несовместных событий равна сумме их вероятностей.
- 34. Пример 1. В урне находятся 30 шаров 10 белых, 15 красных и 5 синих. Найдите вероятность
- 35. Пример 2. В контейнере 10 деталей, из низ 2 нестандартные. Найдите вероятность того, что из 6
- 36. - благоприятные события для А - благоприятные события для В
- 37. Умножение вероятностей. Вероятность совместного появления двух независимых событий равна произведению их вероятностей.
- 38. Пример 1. Монету бросают 3 раза подряд. Какова вероятность, что решка выпадет все три раза. Решение:
- 39. Пример 2. Вероятность попадания в цель при стрельбе из первого орудия равна 0,8, а при стрельбе
- 41. Скачать презентацию





























 Вовка в математическом царстве. Часть 1
Вовка в математическом царстве. Часть 1 Аналитическая геометрия
Аналитическая геометрия Применение симметрии при решении алгебраических задач Учениц 10И класса: Коротковой Анастасии Журавлёвой Дарьи Руководитель:
Применение симметрии при решении алгебраических задач Учениц 10И класса: Коротковой Анастасии Журавлёвой Дарьи Руководитель:  Решение задач с параметрами
Решение задач с параметрами Правовая статистика
Правовая статистика Деление с остатком урок математики, 5 класс
Деление с остатком урок математики, 5 класс Лекция 7. Методы расщепления
Лекция 7. Методы расщепления Десятичные дроби
Десятичные дроби Математический брейн-ринг
Математический брейн-ринг Презентация по математике "Обобщающий урок по теме «Четырехугольники»" - скачать
Презентация по математике "Обобщающий урок по теме «Четырехугольники»" - скачать  Свойства числовых неравенств
Свойства числовых неравенств Аттестационная работа. Образовательная программа элективного курса. За страницами учебника математики. (5 класс)
Аттестационная работа. Образовательная программа элективного курса. За страницами учебника математики. (5 класс) Линейное программирование
Линейное программирование Математические старты
Математические старты Площадь многоугольника
Площадь многоугольника Вычитание из чисел 6, 7. Решение задач
Вычитание из чисел 6, 7. Решение задач Сравнение чисел
Сравнение чисел Состав чисел первого десятка
Состав чисел первого десятка Логическая равносильность формул
Логическая равносильность формул Выпуклость функции. Точки перегиба
Выпуклость функции. Точки перегиба Задачи по математике
Задачи по математике Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена
Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности Уравнение касательной. Условие касания
Уравнение касательной. Условие касания Упрощение выражений
Упрощение выражений Эллипс, гипербола и парабола
Эллипс, гипербола и парабола Тема урока: Арифметическая прогрессия (обобщающий урок) 9 «а» класс Подготовила учитель математики МОУ СОШ №16 Белоконь Наталья В
Тема урока: Арифметическая прогрессия (обобщающий урок) 9 «а» класс Подготовила учитель математики МОУ СОШ №16 Белоконь Наталья В Простейшие тригонометрические уравнения. Задания для устного счета
Простейшие тригонометрические уравнения. Задания для устного счета