- Главная
- Математика
- Задача коммивояжёра

Содержание
- 2. Задача коммивояжёра Общая схема метода ветвей и границ Метод ветвей и границ - общий метод для
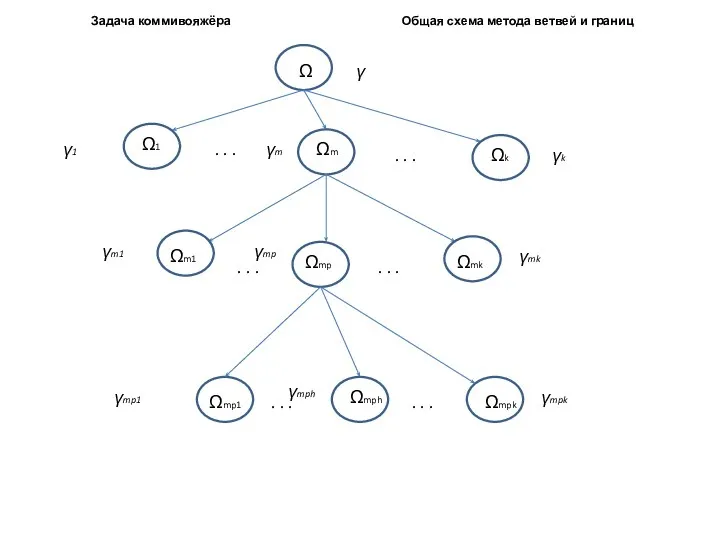
- 3. Задача коммивояжёра Общая схема метода ветвей и границ Ω Ω1 Ωm Ωk . . . .
- 4. Задача коммивояжёра Алгоритм Литтла Алгоритм Литтла является реализацией метода ветвей и границ для задачи коммивояжёра. Правило
- 5. Задача коммивояжёра Алгоритм Литтла Шаг 4. Выбираем нулевой элемент с максимальным штрафом . Разбиваем текущее множество
- 6. Задача коммивояжёра Алгоритм Литтла Шаг 10. Выбранная на шаге 8 вершина соответствует свойству “не включающие дугу
- 7. Задача коммивояжёра Алгоритм Литтла Приводим матрицу по строкам: α1=2, α2=3, α3=2, α4=2, α5=1. Приводим матрицу по
- 8. Задача коммивояжёра Алгоритм Литтла Разбиваем множество всех гамильтоновых циклов на два подмножества Ω1 - “не включающие
- 9. Минимальную нижнюю границу имеет множество Ω2 . Поэтому в матрице C’2 вычисляем штрафы для нулевых элементов:
- 10. В дереве поиска висячие вершины соответсвуют подмножествам Ω1, Ω21 , Ω22 . Минимальную нижнюю границу имеет
- 12. Скачать презентацию
Задача коммивояжёра Общая схема метода ветвей и границ
Метод ветвей и границ
Задача коммивояжёра Общая схема метода ветвей и границ
Метод ветвей и границ
Ветвление состоит в разбиении по некоторому правилу A множества допустимых решений на подмножества
Процедура нахождения оценок заключается в поиске по некоторому правилу B нижних границ для минимальных значений функции f(x) на Пусть полученные нижние границы . Очевидно, .
Из полученных подмножеств выбираем подмножество Ωm, у которого
По правилу A разбиваем Ωm на подмножества
и вычисляем по правилу B нижние границы для минимальных значений функции f(x) на
Задача коммивояжёра Общая схема метода ветвей и границ
Ω
Ω1
Ωm
Ωk
. . .
. .
Задача коммивояжёра Общая схема метода ветвей и границ
Ω
Ω1
Ωm
Ωk
. . .
. .
Ωm1
Ωmp
Ωmk
. . .
γ
. . .
Ωmp1
Ωmph
Ωmpk
. . .
. . .
γ1
γm
γk
γm1
γmp
γmk
γmp1
γmph
γmpk
Задача коммивояжёра Алгоритм Литтла
Алгоритм Литтла является реализацией метода ветвей и границ
Задача коммивояжёра Алгоритм Литтла
Алгоритм Литтла является реализацией метода ветвей и границ
Опишем алгоритм Литтла.
Шаг 1. Приведение матрицы расстояний. Находим в каждой i-ой строке матрицы минимальный элемент αi и вычитаем его из всех элементов этой строки. В полученной матрице в каждом j-ом столбце находим минимальный элемент βj и вычитаем его из всех элементов данного столбца. После проделанных операций получим матрицу C’, каждая строка и каждый столбец которой содержит, по крайней мере, один нуль.
Шаг 2. Вычисляем сумму приводящих констант . Очевидно, что γ является нижней границей для всего множества решений , которое берется в качестве корня дерева поиска и текущего множества решений.
Шаг 3. Для каждого нулевого элемента c’ij = 0 матрицы C’ находим штраф за неиспользование (сумма минимальных элементов в строке и столбце, на пересечении которых стоит нуль, без учёта самого нулевого элемента).
Задача коммивояжёра Алгоритм Литтла
Шаг 4. Выбираем нулевой элемент с максимальным штрафом
Задача коммивояжёра Алгоритм Литтла
Шаг 4. Выбираем нулевой элемент с максимальным штрафом
Разбиваем текущее множество всех гамильтоновых циклов на два подмножества: Ω1 - “не включающие дугу (i,j)” и Ω2 – “включающие дугу (i,j)”. Присоединяем соответсвующие вершины к дереву поиска.
Шаг 5. Вычисляем нижнюю границу γ1 = γ + θij для гамильтоновых циклов подмножества Ω1. Строим соответсвующую Ω1 матрицу расстояний C’1. Для этого значение элемента c’ij заменяем на ∞ и приводим полученную матрицу (неприведенными могут быть только i-ая строка и j-ый столбец, поэтому сумма приводящих констант равна θij) .
Шаг 6. Вычисляем нижнюю границу для гамильтоновых циклов подмножества Ω2. Для этого удаляем из матрицы i-ю строку и j-й столбец, сохраняя исходную нумерацию для оставшихся строк и столбцов, и заменяем на ∞ значение элементов, соответствующих дугам, использование каждой из которых с уже включёнными в гамильтонов цикл дугами, приводит к образованию цикла с числом дуг меньше n. Приводим полученную матрицу, обозначаем её C’2 и добавляем сумму приводящих констант к нижней границе γ множества решений . Получаем нижнюю границу γ2 .
Шаг 7. Если в результате шага 6 получаем матрицу C’2 порядка два и её нижняя граница не превышает границ висячих вершин дерева поиска, то процесс заканчивается, решение найдено, переходим к шагу 11. В противном случае переходим к шагу 8.
Шаг 8. Среди висячих вершин построенного дерева поиска выбираем вершину с наименьшей границей (если таких вершин несколько, выбираем любую из них).
Шаг 9. Если выбранная на шаге 8 вершина соответствует свойству “включающие дугу (i,j)”, то соответствующую ей матрицу расстояний C’2, полученную на шаге 6, берём за С’ и переходим к шагу 3. В противном случае переходим к шагу 10.
Задача коммивояжёра Алгоритм Литтла
Шаг 10. Выбранная на шаге 8 вершина
Задача коммивояжёра Алгоритм Литтла
Шаг 10. Выбранная на шаге 8 вершина
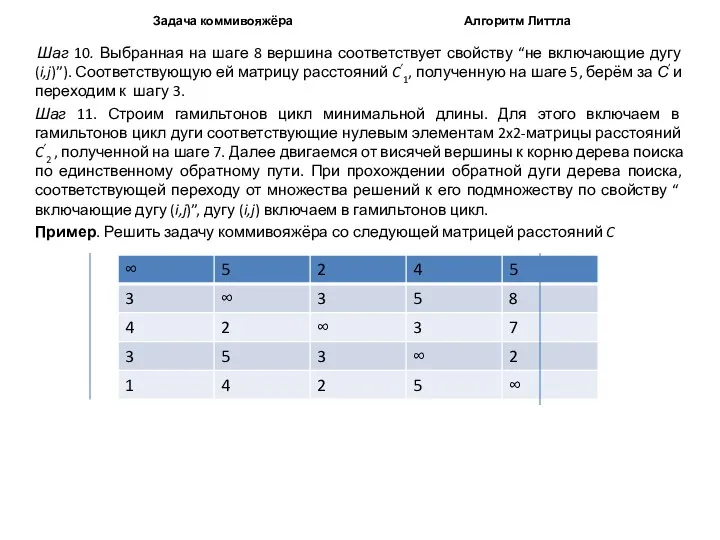
Шаг 11. Строим гамильтонов цикл минимальной длины. Для этого включаем в гамильтонов цикл дуги соответствующие нулевым элементам 2x2-матрицы расстояний C’2 , полученной на шаге 7. Далее двигаемся от висячей вершины к корню дерева поиска по единственному обратному пути. При прохождении обратной дуги дерева поиска, соответствующей переходу от множества решений к его подмножеству по свойству “ включающие дугу (i,j)”, дугу (i,j) включаем в гамильтонов цикл.
Пример. Решить задачу коммивояжёра со следующей матрицей расстояний C
Задача коммивояжёра Алгоритм Литтла
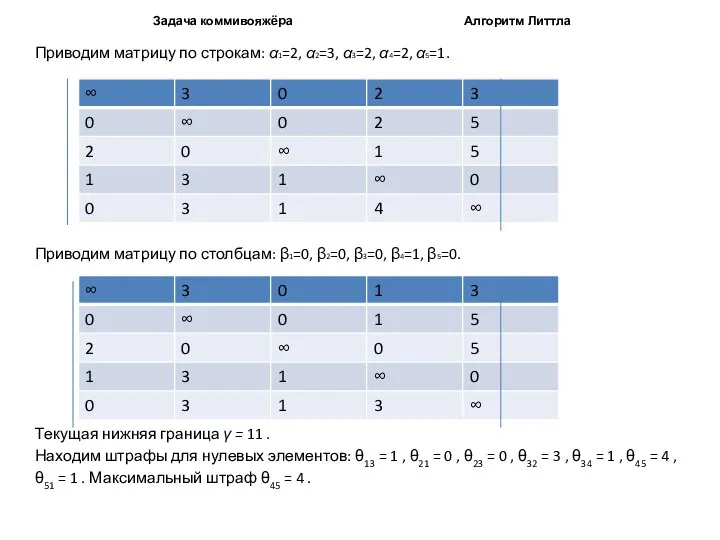
Приводим матрицу по строкам: α1=2, α2=3, α3=2, α4=2,
Задача коммивояжёра Алгоритм Литтла
Приводим матрицу по строкам: α1=2, α2=3, α3=2, α4=2,
Приводим матрицу по столбцам: β1=0, β2=0, β3=0, β4=1, β5=0.
Текущая нижняя граница γ = 11 .
Находим штрафы для нулевых элементов: θ13 = 1 , θ21 = 0 , θ23 = 0 , θ32 = 3 , θ34 = 1 , θ45 = 4 ,
θ51 = 1 . Максимальный штраф θ45 = 4 .
Задача коммивояжёра Алгоритм Литтла
Разбиваем множество всех гамильтоновых циклов на два подмножества
Задача коммивояжёра Алгоритм Литтла
Разбиваем множество всех гамильтоновых циклов на два подмножества
Для второго подмножества матрица расстояний C’2 получается из C’ удалением 4-ой строки и пятого столбца, причём для запрещения образования цикла 4->5->4 , полагаем c’54 = , полученный результат приводим.
Сумма приводящих констант равна 0, следовательно, γ2 = 11 .
Минимальную нижнюю границу имеет множество Ω2 . Поэтому в матрице C’2
Минимальную нижнюю границу имеет множество Ω2 . Поэтому в матрице C’2
θ34 = 1 , θ51 = 1 . Максимальный штраф θ32 = 3 . Разбиваем множество Ω2 на два подмножества Ω21 - “не включающие дугу (3,2)” и Ω22 - “включающие дугу (3,2)”. Для подмножества Ω21 нижняя граница γ21 = 14 . Матрицу расстояний C’21 получим из матрицы C’2 , положив c’32 = и проведя процедуру приведения.
Для подмножества Ω22 матрицу расстояний C’22 получаем из C’2 , удаляя третью строку и второй столбец, затем для запрещения образования цикла 3->2->3 , полагаем c’23= , полученный результат приводим.
Сумма приводящих констант равна 1, следовательно, γ22 = 12 .
Задача коммивояжёра Алгоритм Литтла
В дереве поиска висячие вершины соответсвуют подмножествам Ω1, Ω21 , Ω22
В дереве поиска висячие вершины соответсвуют подмножествам Ω1, Ω21 , Ω22
Возьмём θ13 = 1 . Разбиваем множество Ω22 на два подмножества Ω221 - “не включающие дугу (1,3)” и Ω222 - “включающие дугу (1,3)”. Для подмножества Ω221 нижняя граница γ221 = 13 . Матрицу расстояний C’221 получим из матрицы C’22 , положив c’13 = и проведя процедуру приведения.
Для подмножества Ω222 матрицу расстояний C’222 получаем из C’22 , удаляя первую строку и третий столбец, затем для запрещения образования цикла 1->3->2->1 , полагаем c’21= , полученный результат приводим. Сумма приводящих констант равна 0, следовательно,
γ222 = 12.
В дереве поиска висячие вершины соответсвуют подмножествам Ω1, Ω21 , Ω221 , Ω222 . Минимальную нижнюю границу имеет множество Ω222 . Соответсвующая матрица C’222 имеет размерность 2x2. Следовательно, решение найдено.
Задача коммивояжёра Алгоритм Литтла






 Площади фигур
Площади фигур Симметрия многогранников
Симметрия многогранников Игра – самый умный математик. 6 класс
Игра – самый умный математик. 6 класс Решение квадратных уравнений. Алгебра 8 класс
Решение квадратных уравнений. Алгебра 8 класс Варряд
Варряд Задачи на непрерывные дроби
Задачи на непрерывные дроби Деление. Устный счет
Деление. Устный счет Комплексные числа
Комплексные числа Аксонометрия. (Лекция 1)
Аксонометрия. (Лекция 1) Решение СЛАУ методом Гаусса
Решение СЛАУ методом Гаусса Центральные и вписанные углы
Центральные и вписанные углы Презентация по математике "Метод интервалов" - скачать
Презентация по математике "Метод интервалов" - скачать  Действия с натуральными числами
Действия с натуральными числами Координатный метод решения стереометрических задач
Координатный метод решения стереометрических задач Аттестационная работа. Элективный курс «Производная, её применение»
Аттестационная работа. Элективный курс «Производная, её применение» Построение сечений призмы
Построение сечений призмы Геометрия в жизни человека
Геометрия в жизни человека Корреляционный анализ
Корреляционный анализ Проект «Проценты в нашей жизни»
Проект «Проценты в нашей жизни» Сравнение отрезков и углов
Сравнение отрезков и углов Геометрия в начальной школе
Геометрия в начальной школе Предмет теории вероятностей. Полная группа равновозможных событий. Классическое определение вероятности. Основные формулы
Предмет теории вероятностей. Полная группа равновозможных событий. Классическое определение вероятности. Основные формулы Теория автоматов и формальных языков. Структурный синтез
Теория автоматов и формальных языков. Структурный синтез Контрольная работа №4. Движение
Контрольная работа №4. Движение Функції. Властивості функцій. Перетворення графіків функцій
Функції. Властивості функцій. Перетворення графіків функцій Гаусс, Карл Фридрих
Гаусс, Карл Фридрих Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Уравнения с одним неизвестным
Уравнения с одним неизвестным