Задачи на построение сечений

Сентябрь 16, 2022

Главная
Математика
Задачи на построение сечений

Содержание

2. Секущей плоскостью многогранника называется такая плоскость, по обе стороны от которой есть точки данного многогранника. Сечением
3. Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника есть многоугольник, лежащий в секущей плоскости.
4. Две плоскости пересекаются по прямой (эта аксиома и дала названию метода – под «следом» понимается прямая
5. A B C D B1 C1 D1 M N K Выбираем точки М и N, принадлежащие
6. A B C D B1 C1 D1 M N K A1 E Теперь обращаем внимание, что
7. A B C D B1 C1 D1 M N K A1 E Точки Е и К
8. A B C D B1 C1 D1 M N K A1 E F Далее видим, что
9. A B C D B1 C1 D1 M N K A1 E F G Полученная точка
10. A B C D C1 D1 M N K A1 E F G H Остается соединить
11. Плоскость сечения может задаваться: 1) тремя точками, не лежащими на одной прямой; 2) прямой и точкой,
13. Скачать презентацию

Слайд 2

Секущей плоскостью многогранника называется такая плоскость, по обе стороны от которой

есть точки данного многогранника.
Сечением многогранника называется фигура, состоящая из всех точек, которые являются общими для многогранника и секущей плоскости.

Основные понятия

Слайд 3

Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника есть

многоугольник, лежащий в секущей плоскости. Очевидно, что количество сторон этого многоугольника не может превышать количества граней данного многогранника. Например в пятиугольной призме (всего 7 граней) в сечении могут получиться: треугольник, 4-угольник, 5-угольник, 6-угольник или 7-угольник.

Слайд 4

Две плоскости пересекаются по прямой (эта аксиома и дала названию

метода – под «следом» понимается прямая пересечения какой-либо грани многогранника и секущей плоскости).
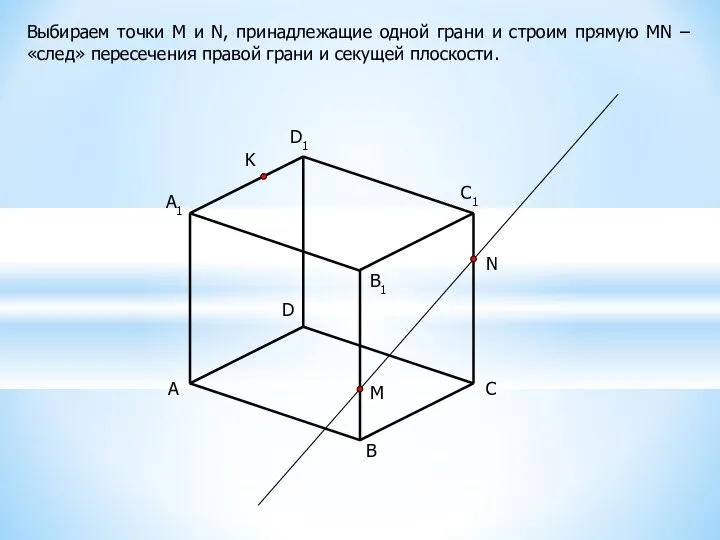
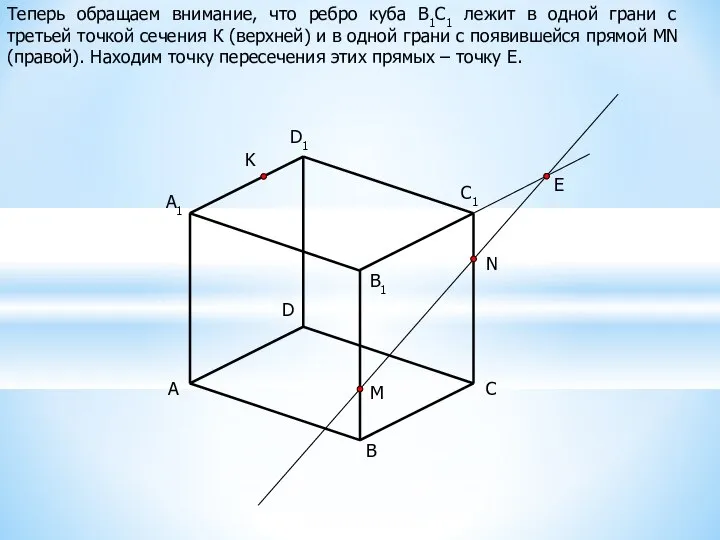
Получение «следа» сводится к получению двух точек, принадлежащих одновременно какой-нибудь грани многогранника и секущей плоскости (подумайте, почему именно двух!?).
Точки получаются как пересечение двух прямых, принадлежащих одной и той же плоскости.
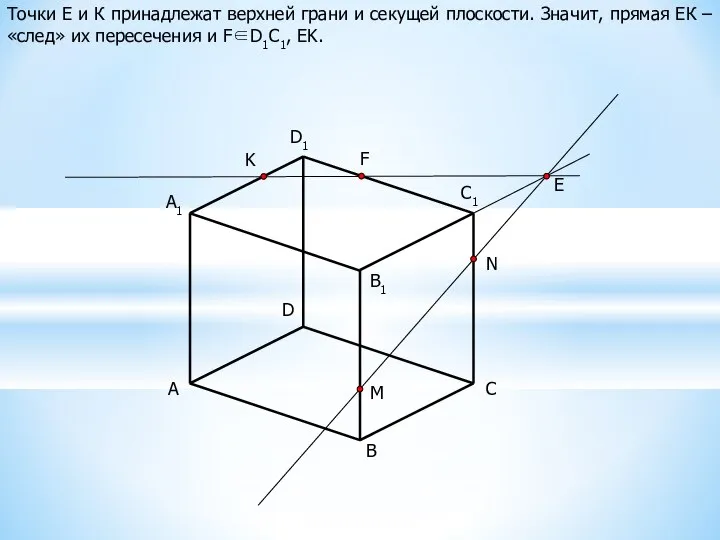
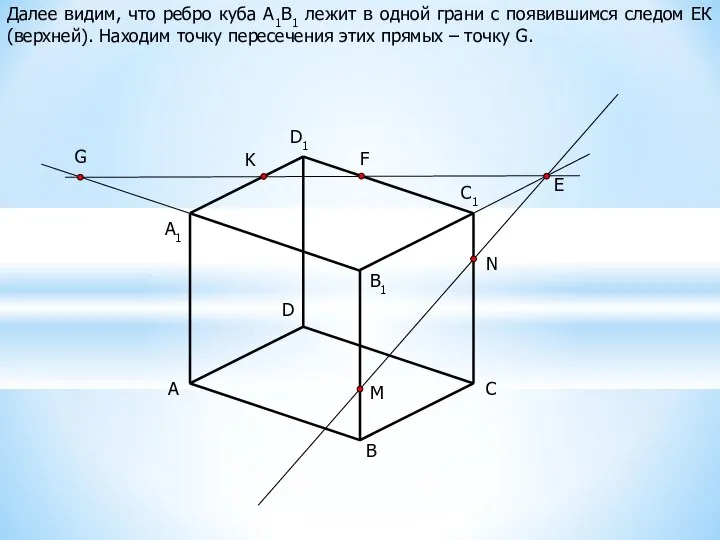
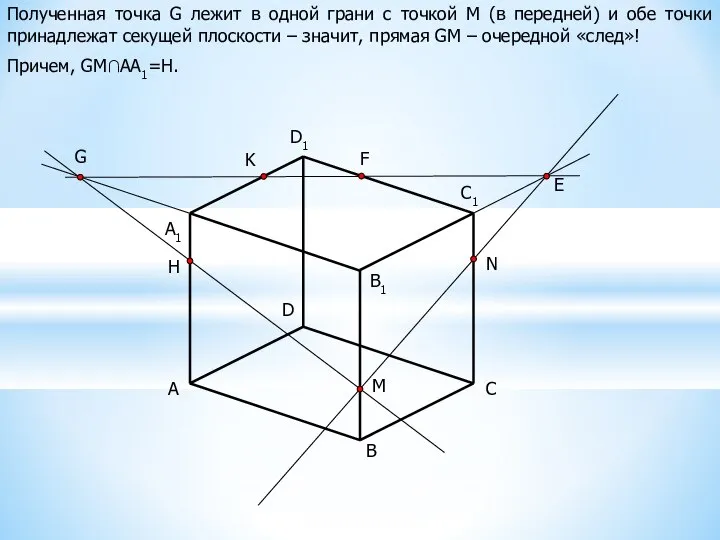
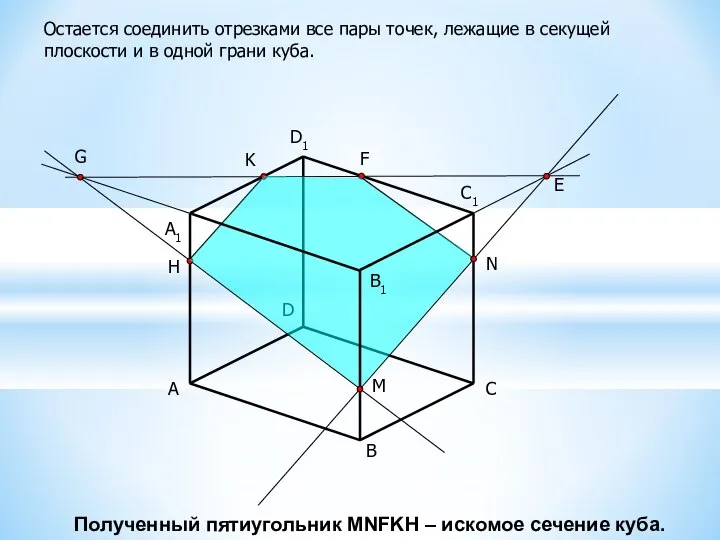
Проследим на примере построение сечения куба плоскостью, заданной тремя данными точками M, N и K.

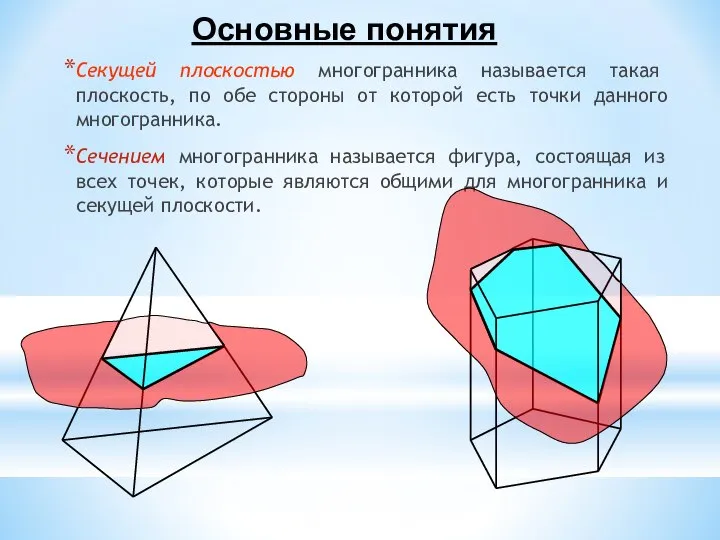
Метод «следов»

Слайд 5

A
B
C
D
B1
C1
D1
M
N
K
Выбираем точки М и N, принадлежащие одной грани и строим прямую

MN – «след» пересечения правой грани и секущей плоскости.

Слайд 6

A
B
C
D
B1
C1
D1
M
N
K
A1
E
Теперь обращаем внимание, что ребро куба В1С1 лежит в одной грани

с третьей точкой сечения К (верхней) и в одной грани с появившейся прямой MN (правой). Находим точку пересечения этих прямых – точку Е.

Слайд 7

A
B
C
D
B1
C1
D1
M
N
K
A1
E
Точки Е и К принадлежат верхней грани и секущей плоскости. Значит,

прямая ЕК – «след» их пересечения и F∈D1C1, EK.

Слайд 8

A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
Далее видим, что ребро куба А1В1 лежит в одной грани с

появившимся следом ЕК (верхней). Находим точку пересечения этих прямых – точку G.

Слайд 9

A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
G
Полученная точка G лежит в одной грани с точкой М (в

передней) и обе точки принадлежат секущей плоскости – значит, прямая GM – очередной «след»!
Причем, GM∩АА1=Н.

Слайд 10

A
B
C
D
C1
D1
M
N
K
A1
E
F
G
H
Остается соединить отрезками все пары точек, лежащие в секущей плоскости и

в одной грани куба.

Полученный пятиугольник MNFKH – искомое сечение куба.

Слайд 11

Плоскость сечения может задаваться:
1) тремя точками, не лежащими на одной

прямой;
2) прямой и точкой, не лежащей на ней;
3) двумя пересекающимися прямыми;
4) двумя параллельными прямыми.
Все эти случаи можно свести к первому, выбирая на прямых удобные для нас точки.

Задачи на построение сечений

Содержание

Секущей плоскостью многогранника называется такая плоскость, по обе стороны от которой

Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника есть

Две плоскости пересекаются по прямой (эта аксиома и дала названию

ABCDB1C1D1MNKВыбираем точки М и N, принадлежащие одной грани и строим прямую

ABCDB1C1D1MNKA1EТеперь обращаем внимание, что ребро куба В1С1 лежит в одной грани

ABCDB1C1D1MNKA1EТочки Е и К принадлежат верхней грани и секущей плоскости. Значит,

ABCDB1C1D1MNKA1EFДалее видим, что ребро куба А1В1 лежит в одной грани с

ABCDB1C1D1MNKA1EFGПолученная точка G лежит в одной грани с точкой М (в

ABCDC1D1MNKA1EFGHОстается соединить отрезками все пары точек, лежащие в секущей плоскости и

Плоскость сечения может задаваться: 1) тремя точками, не лежащими на одной

Похожие презентации