Содержание
- 2. Актуальность: прочное освоение понятия «Система уравнений» создаёт условия для осознанного понимания изложения теории и решения разнообразных
- 3. Цель работы: обобщить научные сведения по теме «Системы уравнений» и познакомиться с новыми способами решения систем
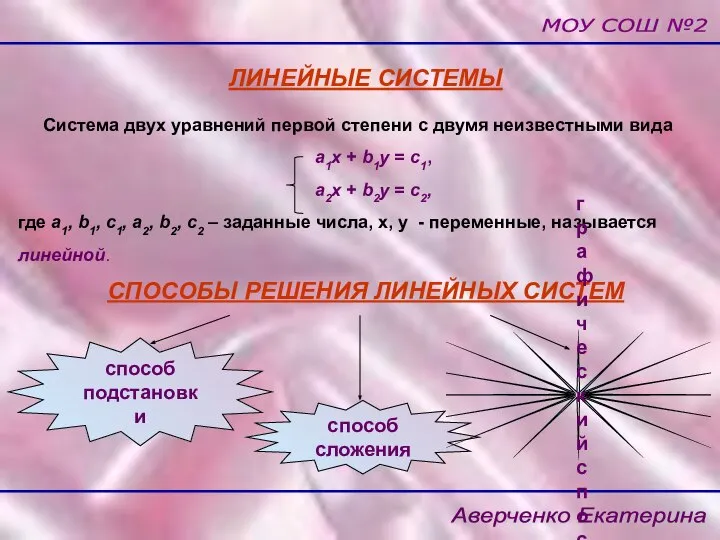
- 4. МОУ СОШ №2 Аверченко Екатерина ЛИНЕЙНЫЕ СИСТЕМЫ Система двух уравнений первой степени с двумя неизвестными вида
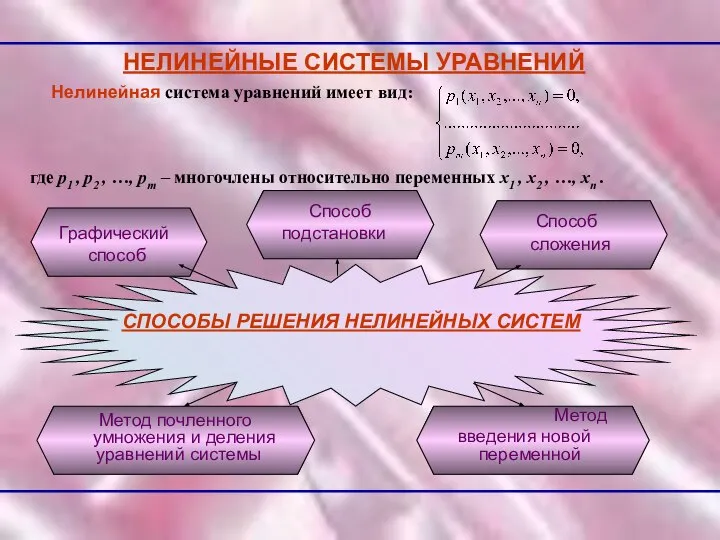
- 5. НЕЛИНЕЙНЫЕ СИСТЕМЫ УРАВНЕНИЙ Нелинейная система уравнений имеет вид: где р1 , р2 , …, рт –
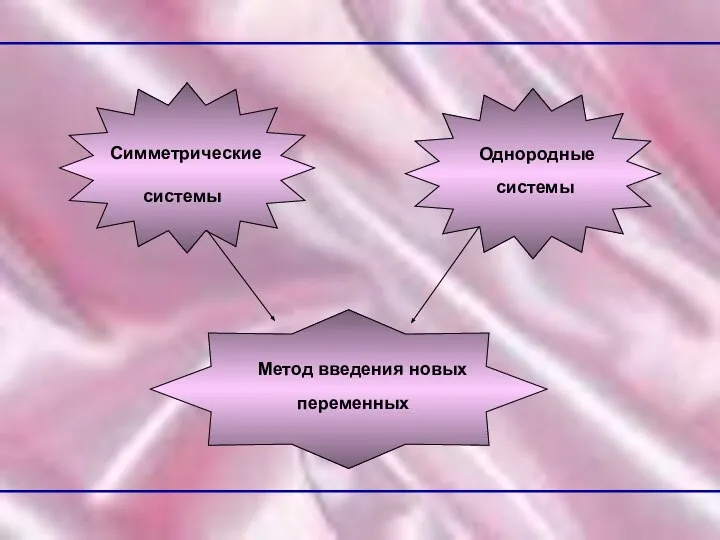
- 6. СИММЕТРИЧЕСКИЕ СИСТЕМЫ УРАВНЕНИЙ Система уравнений Любой симметрический многочлен от переменных х1, х2, …, хn может быть
- 7. ОДНОРОДНЫЕ СИСТЕМЫ УРАВНЕНИЙ При решении однородных уравнений используется замена: х = ty, у = tx При
- 8. Симметрические системы Однородные системы Метод введения новых переменных
- 9. Способ подстановки При решении системы двух линейных уравнений с двумя переменными способом подстановки поступаем следующим образом:
- 10. Графический способ Алгоритм этого метода заключается в следующем: строим графики каждого из уравнений системы; находим координаты
- 11. Способ сложения Суть этого метода такова: уравниваем модули коэффициентов при одном из неизвестных; складывая или вычитая
- 12. Перепишем данную систему в виде: Пример 1. Используя рисунок, находим приближенные значения точек пересечения графиков: (0,4;
- 13. у1 = 5, у2 =0,5, Пример 2. 2у2 – 11у + 5 = 0, Если у
- 14. Пример 3. Решим второе уравнение системы 7у2 - 9у + 2 = 0. Получим у1 =
- 15. Метод почленного умножения и деления уравнений системы перемножаем (делим) уравнения системы почленно, при этом получая более
- 16. Пример 2. Пусть (ху)4 = t (t 0), тогда уравнение примет вид: 6(ху)8 = (ху)8 +
- 17. Метод введения новой переменной Этапы указанного метода: вводится новая переменная только в одно уравнение или две
- 18. 2 . + = 8, у - =1. = t, = z, Пример. Пусть а тогда
- 19. Пример. Пусть х + у = u, ху = v, тогда система уравнений примет вид: Ответ:
- 20. Пример. Если у = 0, то и х = 0, однако х = 0 и у
- 21. Благодарю за внимание
- 23. Скачать презентацию

















 Управляющая компания Cosmoservice
Управляющая компания Cosmoservice Матрица для расчетов рационов для бройлеров с ЛисофортомТМ Сухим
Матрица для расчетов рационов для бройлеров с ЛисофортомТМ Сухим Красота фигуры человека в движении
Красота фигуры человека в движении Оценка разрешающей способности малоглубинной сейсморазведки при определении глубины залегания скальных пород
Оценка разрешающей способности малоглубинной сейсморазведки при определении глубины залегания скальных пород презентация Гераськина Аня 26.03
презентация Гераськина Аня 26.03 Организация вспомогательного производства
Организация вспомогательного производства Стратегический менеджмент. Актуальные вопросы разработки стратегии для растущих компаний
Стратегический менеджмент. Актуальные вопросы разработки стратегии для растущих компаний Бардовские песни
Бардовские песни Культурно-религиозные традиции в международных отношениях
Культурно-религиозные традиции в международных отношениях Повышение стабильности качества контактной сварки за счёт исследования электрических и тепловых процессов
Повышение стабильности качества контактной сварки за счёт исследования электрических и тепловых процессов 20140515_okh_uzh_eti_ekzameny2
20140515_okh_uzh_eti_ekzameny2 Известные актеры (фотографии)
Известные актеры (фотографии) Транспорт будущего
Транспорт будущего How works “adding item to pedidos”
How works “adding item to pedidos” Положение рук в мексиканском танце
Положение рук в мексиканском танце Бизнес-план. Вышивка
Бизнес-план. Вышивка Настольная игра Доббль
Настольная игра Доббль Древесно-стружечные плиты (ДСП)
Древесно-стружечные плиты (ДСП) Медицинский_туризм_в_Армении_ENGLISHH
Медицинский_туризм_в_Армении_ENGLISHH Фурнитура для пластиковых и деревянных окон Vorne
Фурнитура для пластиковых и деревянных окон Vorne Электрические машины переменного тока
Электрические машины переменного тока Кроссворд Витамины на грядке
Кроссворд Витамины на грядке szxdcfgvbhjj
szxdcfgvbhjj ТК АНАЛИЗ ЭПИЗОДА
ТК АНАЛИЗ ЭПИЗОДА Мы-наследники Победы!
Мы-наследники Победы! Динамическая оценка рисков, одиночные работы, изменения в глобальном стандарте по оценке рисков и рутинные задачи
Динамическая оценка рисков, одиночные работы, изменения в глобальном стандарте по оценке рисков и рутинные задачи Технология возведения крупнопанельных зданий. (Лекция 4)
Технология возведения крупнопанельных зданий. (Лекция 4) Cheap restaurants
Cheap restaurants