Содержание
- 2. Обозначим через длину кратчайшего пути из vi в vj с промежуточными вершинами во множестве {v1,…,vm}. Алгоритм
- 3. 2) 3) Длина кратчайшего пути из вершины vi в вершину vj: Алгоритм строит матрицу за n
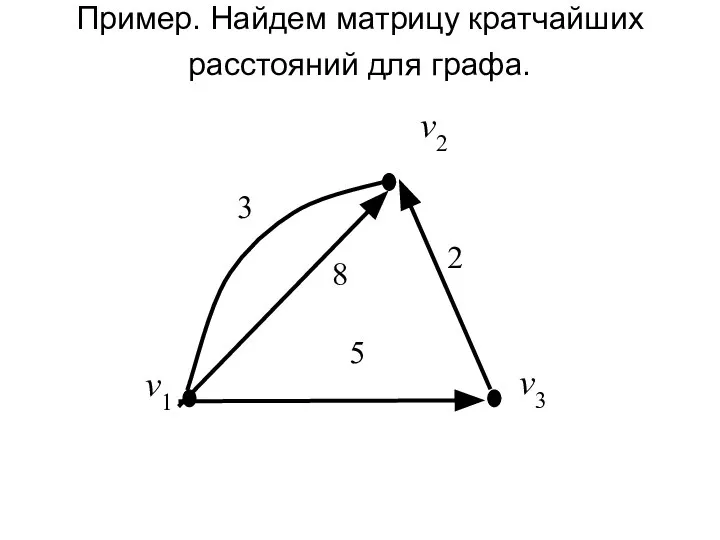
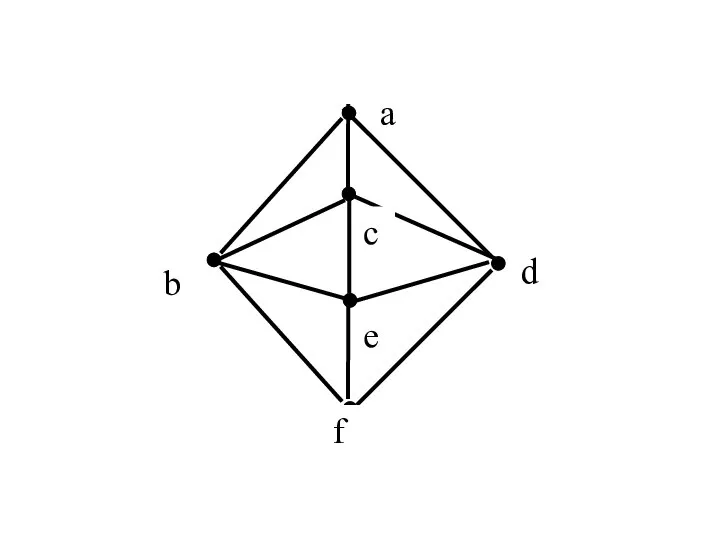
- 4. Пример. Найдем матрицу кратчайших расстояний для графа. v1 5
- 5. v1 v2 v3
- 6. Элементы матрицы D(1) находим по правилу:
- 8. Элементы матрицы D(2) находим по правилу:
- 10. Элементы матрицы D(3) находим по правилу:
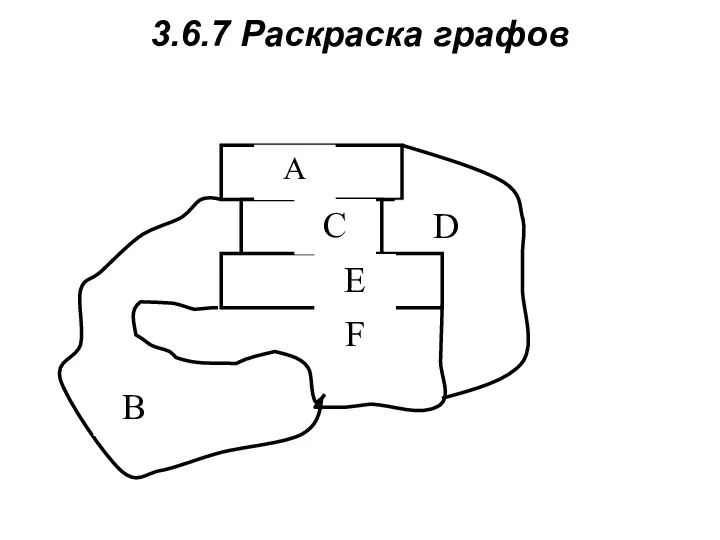
- 13. 3.6.7 Раскраска графов
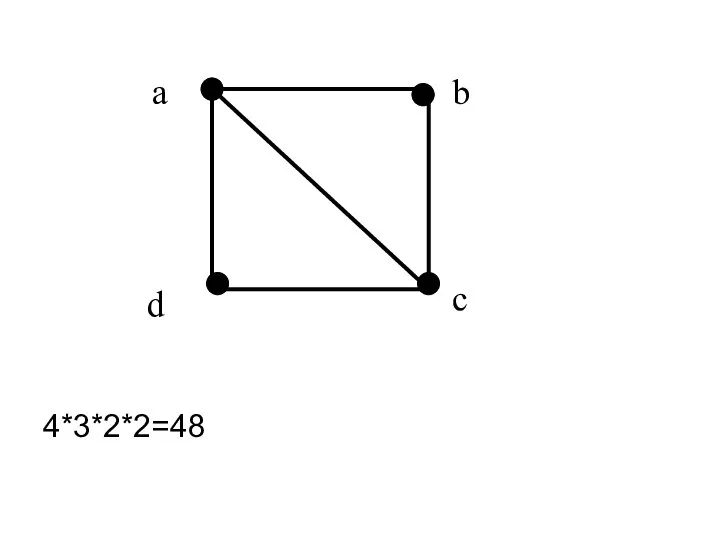
- 15. 4*3*2*2=48
- 16. Раскраской графа G называется окрашивание вершин графа G, такое, что никакие две смежные вершины не окрашены
- 18. Скачать презентацию


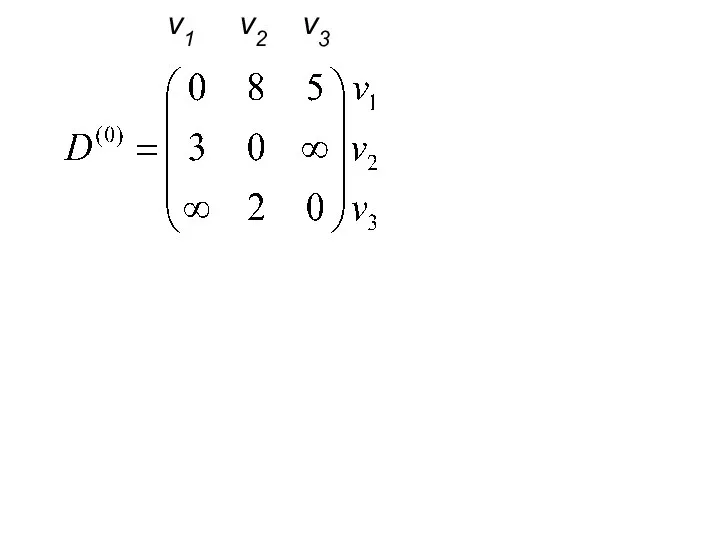

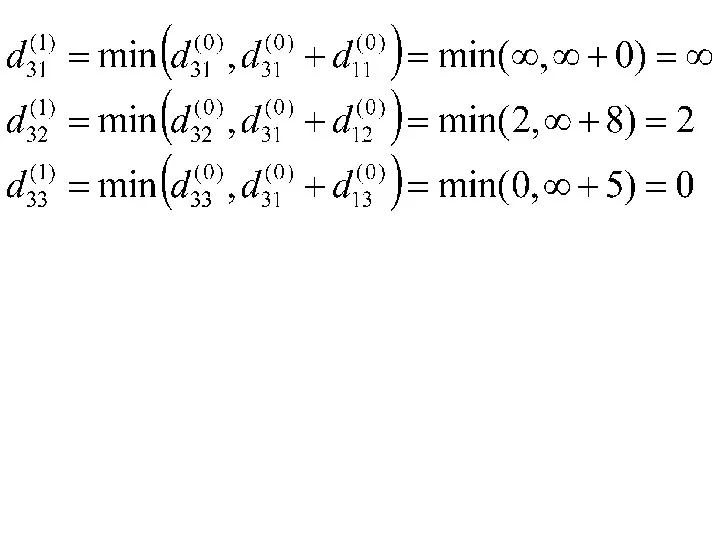
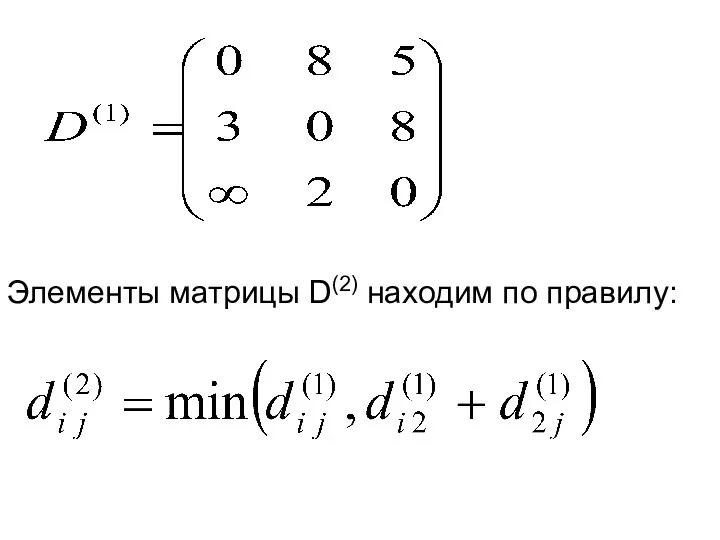
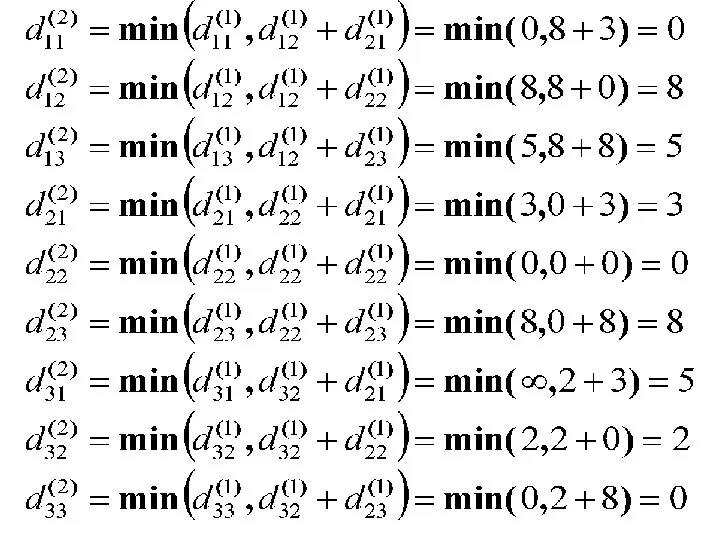

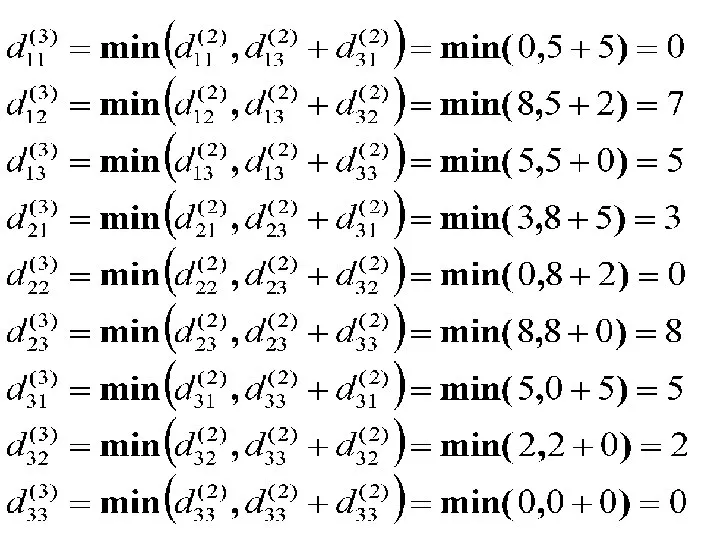
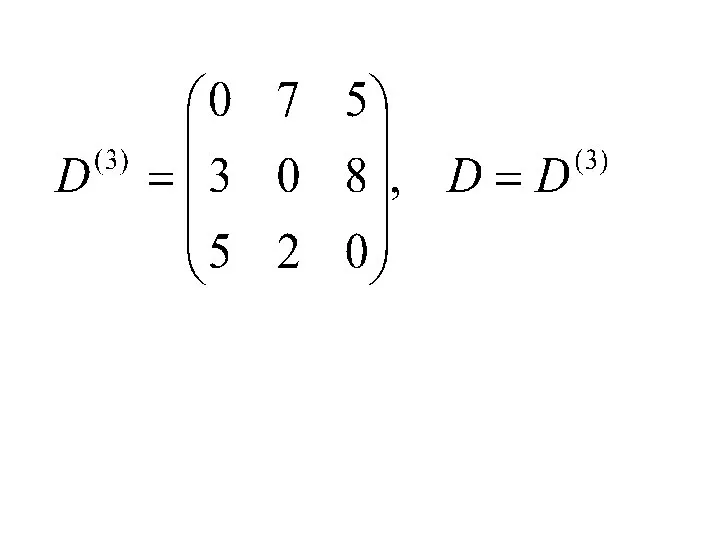

 Малинина Алена Викторовна Учитель черчения и изобразительного искусства МОУ « СОШ № 12» город Усолье-Сибирс
Малинина Алена Викторовна Учитель черчения и изобразительного искусства МОУ « СОШ № 12» город Усолье-Сибирс Прием документации и зачисление в организации образования
Прием документации и зачисление в организации образования Ваш праздник
Ваш праздник Компьютерные сети
Компьютерные сети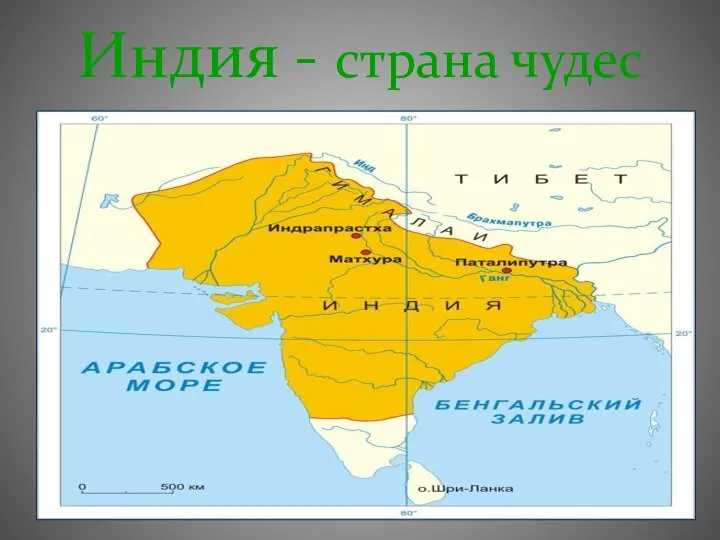 Культура Древней Индии
Культура Древней Индии Учитель английского языка Евсюкова И.А. МОУ «Федчёвская ООШ» 2009 год
Учитель английского языка Евсюкова И.А. МОУ «Федчёвская ООШ» 2009 год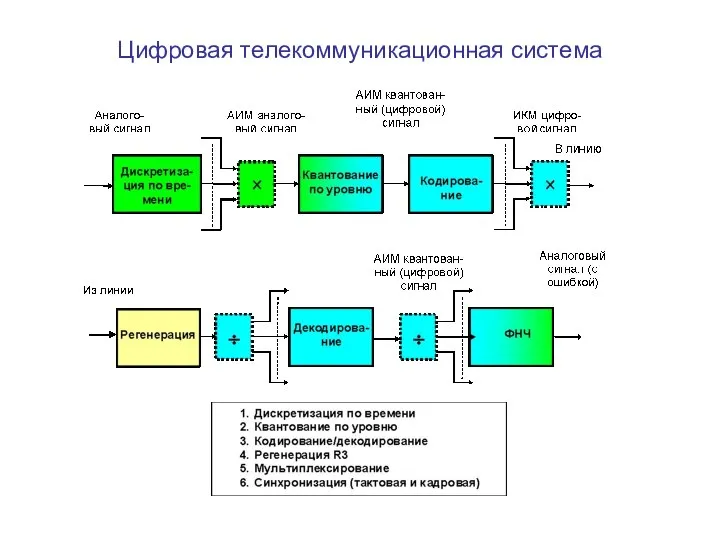 Цифровая телекоммуникационная система
Цифровая телекоммуникационная система Понятие гражданского права, как отрасли права. Источники гражданского права
Понятие гражданского права, как отрасли права. Источники гражданского права Передача информации. Локальные компьютерные сети
Передача информации. Локальные компьютерные сети Плазмозаменители
Плазмозаменители Амнистия. Помилование.Судимость.
Амнистия. Помилование.Судимость. Классы
Классы  Вода и водные устройства
Вода и водные устройства Проект по продвижению комплекса ГТО
Проект по продвижению комплекса ГТО Презентация на тему "Образовательные программы" - скачать презентации по Педагогике
Презентация на тему "Образовательные программы" - скачать презентации по Педагогике Сервисы в Android
Сервисы в Android Элементарные функции
Элементарные функции Компьютерные вирусы
Компьютерные вирусы «МЫ ВЫБИРАЕМ ЗДОРОВЬЕ!!!» «Скажи наркотикам НЕТ !!!» Один мыслитель гулял со своими учениками в саду и отвечал на их вопросы. Потом к
«МЫ ВЫБИРАЕМ ЗДОРОВЬЕ!!!» «Скажи наркотикам НЕТ !!!» Один мыслитель гулял со своими учениками в саду и отвечал на их вопросы. Потом к  XXIII Зимние Олимпийские игры
XXIII Зимние Олимпийские игры Модель методической работы школы на 2011-2012 гг. Цели: активизировать методическую работу школы способствовать повышению професс
Модель методической работы школы на 2011-2012 гг. Цели: активизировать методическую работу школы способствовать повышению професс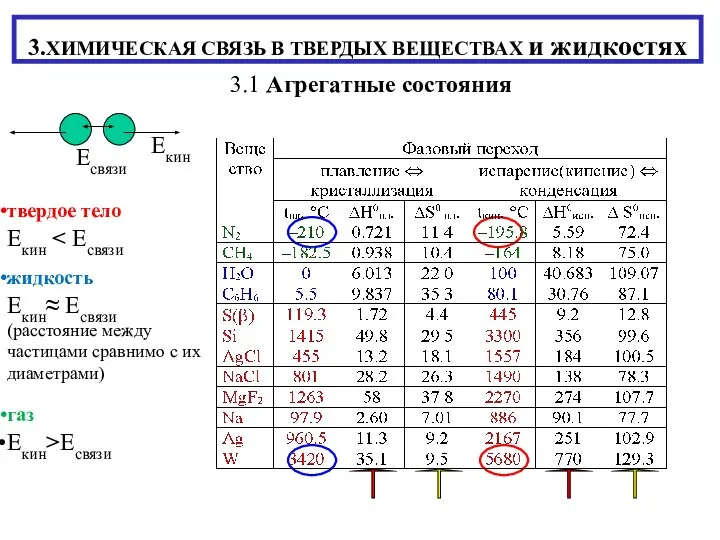 ХИМИЧЕСКАЯ СВЯЗЬ В ТВЕРДЫХ ВЕЩЕСТВАХ и жидкостях
ХИМИЧЕСКАЯ СВЯЗЬ В ТВЕРДЫХ ВЕЩЕСТВАХ и жидкостях Содержание и ремонт цементобетонных покрытий
Содержание и ремонт цементобетонных покрытий Презентация_____
Презентация_____ Разгледайте изразите. В какъв ред ще се извършват действията? Пресметнете ги. 516 – 7. 9 = 115 + 65 : 5 = 1 205. 78 – 96 : 2 = 2 015. 2 – 3 348 : 31 = - презента
Разгледайте изразите. В какъв ред ще се извършват действията? Пресметнете ги. 516 – 7. 9 = 115 + 65 : 5 = 1 205. 78 – 96 : 2 = 2 015. 2 – 3 348 : 31 = - презента Конституционное право РФ
Конституционное право РФ Укажите, в каком случае слово употреблено в прямом значении, а в каком – в переносном. Подберите и запишите синонимы к данным слова
Укажите, в каком случае слово употреблено в прямом значении, а в каком – в переносном. Подберите и запишите синонимы к данным слова Презентация на тему "Управление качество образования в МОУ Лебяженской СОШ Краснотуранского района" - скачать презентации по
Презентация на тему "Управление качество образования в МОУ Лебяженской СОШ Краснотуранского района" - скачать презентации по