Содержание
- 2. Задачи сетевого управления При решении задачи сетевого управления стремятся получать максимально полезный результат, как по точности
- 3. При синтезе оптимального управления необходимо: знать законы распределения вероятностей и необходимые статистические характеристики случайных возмущений, что
- 4. Стохастическая система dx/dt=A(t)x(t) + Вu(t)+C(t)ξ(t) Вu(t) – управление системой C(t)ξ(t) – гауссовый белый шум Автономная система
- 5. Методы формирования управления в динамических системах Оценка качества управления системы Теорема о разделении для управляемых систем.
- 6. Анализ состояния управляемых систем. Инерционность системы определяется А и зависит от параметров системы и условиями: локальная
- 7. Теорема о разделении для управляемых систем. В стохастических системах оптимальное управление может быть построено с помощью
- 8. Оценка качества управления системы Оценка зависит от целевой установки системы. Система связи направленная на предоставления обслуживания
- 9. Задание и варианты Реализовать алгоритм уравнения состояния - функция прогноза , где Параметры: - относительная величина
- 10. Задание №2 Выполнить: Построить график оценки на 1000 шагах. Определить наличие свойств устойчивости процедуры. Определить интервал,
- 11. Программа Matlaba clear all; clc; N=1000; t1=1:N; D=10; T=1; T0=1000; % shag diskretizatii v=randn(size(t1)); w=randn(size(t1)); m=ones(size(t1));
- 12. Построить график реализации Определить выборочное среднее и дисперсию: M = 0.0068, D = 0.9605 Гистограмму распределения
- 14. Скачать презентацию
Задачи сетевого управления
При решении задачи сетевого управления стремятся получать максимально полезный
Задачи сетевого управления
При решении задачи сетевого управления стремятся получать максимально полезный
ы критерия качества системы , например, минимум среднего
ы квадрата времени задержки.
Кроме того, обычно оценивается чувствительность синтезированной системы управления к отклонениям реальных параметров и характеристик действующих возмущений (так называемая задача исследования чувствительности модели).
Обязательным так же является исследование устойчивости управления, в рамках диапазонов изменений, которые предстоит иметь в результате функционирования управляемой системы.
Необходимо также исследовать границы устойчивой работы, чтобы иметь представление о том, насколько близко может подходит система к опасному хаотическому режиму.
При синтезе оптимального управления необходимо:
знать законы распределения вероятностей и необходимые статистические
При синтезе оптимального управления необходимо:
знать законы распределения вероятностей и необходимые статистические
наблюдать (контролировать) фазовые координаты объекта управления и данные об их изменении в процессе управления;
определить ограничения, которые налагаются на систему управления, (границы допустимых управлений, данные по критическому трафику в ЧНН и др.).
Стохастическая система
dx/dt=A(t)x(t) + Вu(t)+C(t)ξ(t)
Вu(t) – управление системой
C(t)ξ(t) – гауссовый белый шум
Стохастическая система
dx/dt=A(t)x(t) + Вu(t)+C(t)ξ(t)
Вu(t) – управление системой
C(t)ξ(t) – гауссовый белый шум
Автономная система
dx/dt=A(t)x(t)
A – определяет устойчивость системы
Управление – переход с одной точки координат в другую (х0→х1). Время управления зависит от инерционных свойств системы.
Стохастическая и автономная системы
Для стохастической системы переход с исходной точки х0 осуществляется по сложной случайной траектории. Конечная точка – область, размеры которой определяются случайным возмещунием.
Методы формирования управления в динамических системах
Оценка качества управления системы
Теорема о разделении
Методы формирования управления в динамических системах
Оценка качества управления системы
Теорема о разделении
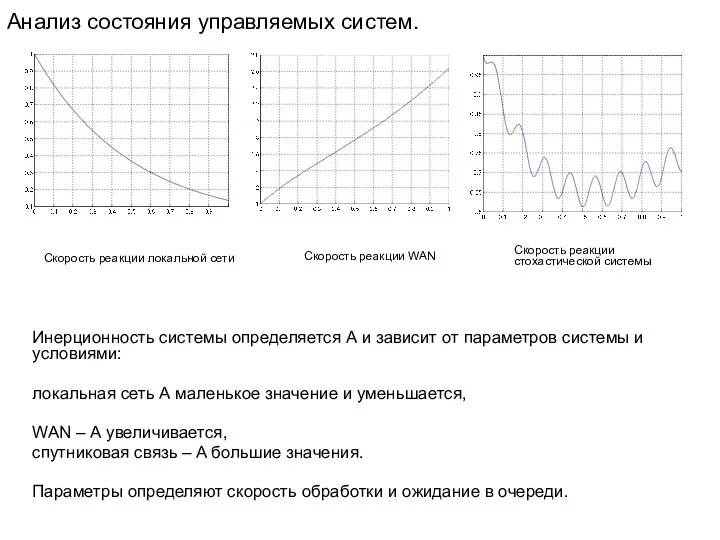
Анализ состояния управляемых систем.
Анализ состояния управляемых систем.
Инерционность системы определяется А и зависит от параметров
Анализ состояния управляемых систем.
Инерционность системы определяется А и зависит от параметров
локальная сеть А маленькое значение и уменьшается,
WAN – А увеличивается,
спутниковая связь – A большие значения.
Параметры определяют скорость обработки и ожидание в очереди.
Скорость реакции локальной сети
Скорость реакции WAN
Скорость реакции стохастической системы
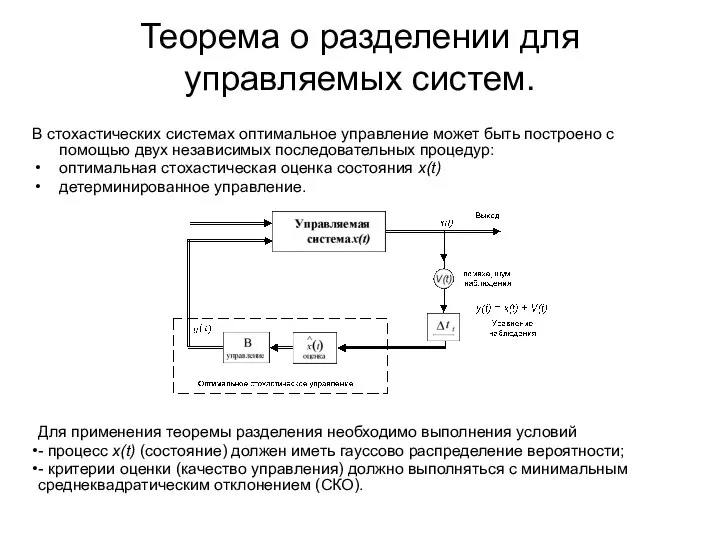
Теорема о разделении для управляемых систем.
В стохастических системах оптимальное управление может
Теорема о разделении для управляемых систем.
В стохастических системах оптимальное управление может
оптимальная стохастическая оценка состояния x(t)
детерминированное управление.
Для применения теоремы разделения необходимо выполнения условий
- процесс x(t) (состояние) должен иметь гауссово распределение вероятности;
- критерии оценки (качество управления) должно выполняться с минимальным среднеквадратическим отклонением (СКО).
Оценка качества управления системы
Оценка зависит от целевой установки системы. Система связи
Оценка качества управления системы
Оценка зависит от целевой установки системы. Система связи
Оптимальным считается такое управление, когда достигается максимально возможное качество функционирования системы.
Система чаще всего описывается несколькими критериями. Поэтому при предоставлении качества решается многокритериальная задача.
Метод компромиссов: один критерий обеспечивается максимальным (минимальным), а остальные фиксируются;
Метод взвешивания критериев. К=∑Кiwi , wi – вес критериев, выбирается исходя из значимости критерия.
Превосходной называется такая система, котороя максимальна по всем критериям.
Критерий среднеквадратического отклонения. КСКО=(х-х0)2 → min
Задание и варианты
Реализовать алгоритм уравнения состояния
- функция прогноза , где
Параметры:
Задание и варианты
Реализовать алгоритм уравнения состояния
- функция прогноза , где
Параметры:
- с.п.м. порождающего шума
Выполнить:1. Построить график реализации на 1000 шагах.
2. Определить выборочное среднее и дисперсию. Сравнить с заданными.
3. Построить гистограмму распределения и показать возможность ее гауссовой аппроксимации4. Построить выборочную корреляционную функцию. Определить выборочный интервал корреляции реализации . Сравнить полученные данные с заданными
Варианты выбираются согласно последних цифр номера зачетной книги.
Задание №2
Выполнить:
Построить график оценки на 1000 шагах.
Определить наличие свойств устойчивости процедуры.
Определить
Задание №2
Выполнить:
Построить график оценки на 1000 шагах.
Определить наличие свойств устойчивости процедуры.
Определить
Найти выборочное значение дисперсии ошибки оценки по формуле .
Дать выводы о качестве оценки (смещенная, несмещенная) и о качестве алгоритма (скорость сходимости, остаточная погрешность, влияние уровня шума , влияние шага дискретизации по отношению к )
Получить оценку
по алгоритму стохастической аппроксимации Роббинса-Монро:
,
,
– шум в канале наблюдения.
где
Программа Matlaba
clear all; clc;
N=1000;
t1=1:N;
D=10;
T=1;
T0=1000; % shag
Программа Matlaba
clear all; clc;
N=1000;
t1=1:N;
D=10;
T=1;
T0=1000; % shag
v=randn(size(t1));
w=randn(size(t1));
m=ones(size(t1));
% ---------------------------------
% issledovanie slu4aynoy posledovatelnosti
% --------------------------------
figure (1) % grafik slu4aynoy posledovatelnosti
plot (t1,w)
grid on
M=mean(w);
D=mean((w-M).^2);
[aa,bb]=hist(w,20);
dx=(max(w)-min(w))/20;
p1=aa/(N);%*dx
mx=bb*p1';
sigm=sqrt(mean ((w-mx).^2));
p2=exp(-(bb-mx).^2/(2*sigm^2))/(sigm*sqrt(2*pi))*dx;
M % mat ogidanie
D % dispersiya
figure (2) % histogramma slu4aynoy posledovatelnosti
bar(bb,p1)
grid on
hold on, plot(bb,p2,'r')
title('Histogram signal')
% korfunkciya -------------
R=zeros(size(t1));
for t=1:20
for k=1:(N-20)
R(t)=R(t)+w(k)*w(k+t-1);
end;
R(t)= R(t)/(N-20);
end;
R=R/max(R);
mm=0:(N-1);
figure(22)
plot(mm,R)
xlabel('tau')
ylabel('R(tau)')
title('Kor funktiya SP')
grid on
S=fft(R,512);
W=(0:255)/256*(1000000/2);
% ---------------------
% ---------------------------------
% formorovanie vhodnogo signala
% --------------------------------
x(1)=0;
F=exp(-T/T0);
G=sqrt(D*F*(1-F));
for k=1:N-1
x(k+1)=F*x(k)+G*w(k);
end
% issledovanie vhodnogo signala
figure(3)
plot(t1(1:1000),x(1:1000));
grid
title('vhodnoy signal')
M=mean(x);
D=mean((x-M).^2);
Mvx=M
Dvx=D
[aa,bb]=hist(x,20);
dx=(max(x)-min(x))/20;
p1=aa/(N);%*dx
mx=bb*p1';
sigm=sqrt(mean ((x-mx).^2));
p2=exp(-(bb-mx).^2/(2*sigm^2))/(sigm*sqrt(2*pi))*dx;
figure (4) % histogramma
bar(bb,p1)
grid on
hold on, plot(bb,p2,'r')
title('Histogram signal x')
% korfunkciya -------------
R=zeros(size(t1));
for t=1:20
for k=1:(N-20)
R(t)=R(t)+x(k)*x(k+t-1);
end;
R(t)= R(t)/(N-20);
end;
R=R/max(R);
mm=0:(N-1);
figure(44)
plot(mm,R)
xlabel('tau')
ylabel('R(tau)')
title('Kor funktiya signala')
grid on
S=fft(R,512);
W=(0:255)/256*(1000000/2);
% ---------------------
% signal+shum
x(1)=0;
F=exp(-T/T0);
G=sqrt(D*F*(1-F));
H=1;
C1=0.4;
l=10;
S=0.09;
for k=1:N-1
m(k)=C1*sin(l*k*T/T0);
x(k+1)=S*F*x(k)+G*w(k)+m(k);
end
% -------------------------
% issledovanie signal+shum
% -------------------------
figure(5)
plot(t1(1:1000),x(1:1000));
grid
title('signal+shum')
M=mean(x);
D=mean((x-M).^2);
Mss=M
Dss=S
% korfunkciya -------------
R=zeros(size(t1));
for t=1:20
for k=1:(N-20)
R(t)=R(t)+x(k)*x(k+t-1);
end;
R(t)= R(t)/(N-20);
end;
R=R/max(R);
mm=0:(N-1);
figure(33)
plot(mm,R)
xlabel('tau')
ylabel('R(tau)')
title('Kor funktiya na vx')
grid on
S=fft(R,512);
W=(0:255)/256*(1000000/2);
% ---------------------
[aa,bb]=hist(x,20);
dx=(max(x)-min(x))/20;
p1=aa/(N);%*dx
mx=bb*p1';
sigm=sqrt(mean ((x-mx).^2));
p2=exp(-(bb-mx).^2/(2*sigm^2))/(sigm*sqrt(2*pi))*dx;
figure (6) % histogramm signal+shum
bar(bb,p1)
grid on
hold on, plot(bb,p2,'r')
title('Histogram signal+shum')
% uravnenie nabluydenia
z=H*x+v+C1*m;
% grafik nablyudeniya
figure(7)
plot(t1(1:1000),z(1:1000));
grid
title('Grafik nablyudeniya')
% -----------------------------------------
% ocenka Robbinsa-Monro
% ----------------------------------------
Vw=2*ones(size(t1));
Vv=2*ones(size(t1));
Vx(1)=1;
V1x(1)=1;
K=0.1;
x1(1)=F*0;
er3(1)=1;
for k=2:N
Vx(k)=F*V1x(k-1)*F'+G*Vw(k)*G';
V1x(k)=(1-K*H)*Vx(k);
x1(k)=F*x1(k-1)+K*(z(k-1)-H*F*x1(k-1));
er3(k)=z(k-1)-H*F*x1(k-1);
n(k)=x(k)-x1(k);
end
er=(x-x1); % oshibka ocenki
er1m=mean(er);
er1=mean((er-er1m).^2)
% issledovanie vyhodnogo signala
figure(8)
subplot(211)
plot(t1(1:1000), x1(1:1000),'r'); % ocenka signala
grid
hold on
title('signal na vyhode')
subplot(212)
plot(t1(1:1000),er(1:1000),'m'); % oshibka ocenki
grid
title('oshibka ocenki')
M=mean(x1);
D=mean((x1-M).^2);
Moc=M
Doc=D
% korfunkciya -------------
R=zeros(size(t1));
for t=1:20
for k=1:(N-20)
R(t)=R(t)+x1(k)*x1(k+t-1);
end;
R(t)= R(t)/(N-20);
end;
R=R/max(R);
mm=0:(N-1);
figure(33)
plot(mm,R)
xlabel('tau')
ylabel('R(tau)')
title('Kor funktiya na vux')
grid on
S=fft(R,512);
W=(0:255)/256*(1000000/2);
% ---------------------
[aa,bb]=hist(x1,20);
dx=(max(x1)-min(x1))/20;
p1=aa/(N);%*dx
mx=bb*p1';
sigm=sqrt(mean ((x1-mx).^2));
p2=exp(-(bb-mx).^2/(2*sigm^2))/(sigm*sqrt(2*pi))*dx;
figure (9) % Histogram signal
bar(bb,p1)
grid on
hold on, plot(bb,p2,'r')
title('Histogram signal')
%---------------------------------
figure(10)
plot(t1(1:200),V1x(1:200)); % korfunkciyz signala na vyhode
hold on
grid
title('Korfunkciya signala na vyhode')
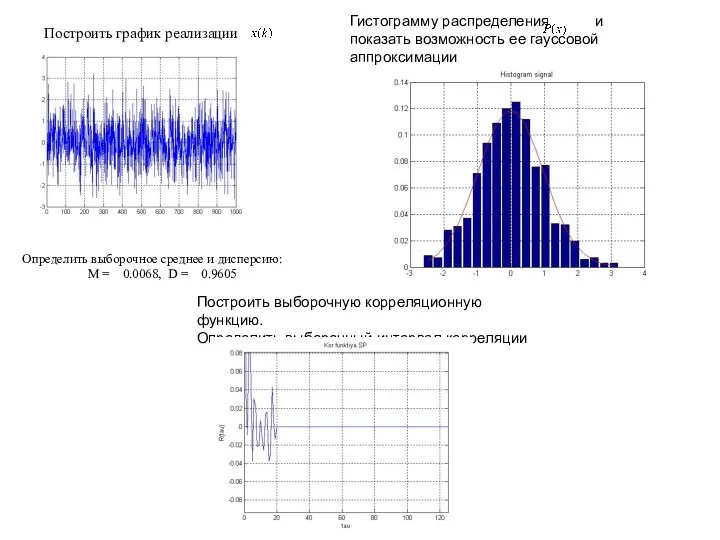
Построить график реализации
Определить выборочное среднее и дисперсию:
M =
Построить график реализации
Определить выборочное среднее и дисперсию:
M =
Гистограмму распределения и
показать возможность ее гауссовой аппроксимации
Построить выборочную корреляционную функцию.
Определить выборочный интервал корреляции








 Ілияс Есенберлин “ Қаһар” романы тіліндегі кездесетін диалектілік ерекшеліктер
Ілияс Есенберлин “ Қаһар” романы тіліндегі кездесетін диалектілік ерекшеліктер Easter egg hunt!
Easter egg hunt! Латинский язык Имя прилагательное. Словарная форма
Латинский язык Имя прилагательное. Словарная форма Бизнес – проект по развитию садоводства
Бизнес – проект по развитию садоводства Субъекты процедур банкротства
Субъекты процедур банкротства Власть. Структурная и ситуационная власть
Власть. Структурная и ситуационная власть Мировая художественная культура
Мировая художественная культура Регистры. Определение, применение, состав, виды
Регистры. Определение, применение, состав, виды СТРАТЕГИЧЕСКИЙ ПРОЕКТ «ГОСТИНИЦЫ ЕКАТЕРИНБУРГА» Докладчик – Председатель Комитета по организации бытового обслуживания на
СТРАТЕГИЧЕСКИЙ ПРОЕКТ «ГОСТИНИЦЫ ЕКАТЕРИНБУРГА» Докладчик – Председатель Комитета по организации бытового обслуживания на Архитектура Древней Руси
Архитектура Древней Руси Зимушка -зима
Зимушка -зима  Сложение гармонических колебаний
Сложение гармонических колебаний  Розробка Android-додатку “PDF читач”
Розробка Android-додатку “PDF читач” Складирование конструкций
Складирование конструкций Презентация на тему "Ключевые компетенции учителя" - скачать презентации по Педагогике
Презентация на тему "Ключевые компетенции учителя" - скачать презентации по Педагогике Баскетбольный турнир в детском саду "Оранжевый мяч"
Баскетбольный турнир в детском саду "Оранжевый мяч" Основы триботехники. Лекция 1
Основы триботехники. Лекция 1 Изобразительное искусство – средство познания себя и мира Картавцева О.Д.- к.п.н., доцент кафедры изобразительного искусства
Изобразительное искусство – средство познания себя и мира Картавцева О.Д.- к.п.н., доцент кафедры изобразительного искусства Модели деловой карьеры менеджера
Модели деловой карьеры менеджера Калькуляция себестоимости с полным распределением затрат и по переменным издержкам
Калькуляция себестоимости с полным распределением затрат и по переменным издержкам Предмет і методи політології. Політика як соціальне явище
Предмет і методи політології. Політика як соціальне явище Изменения в нормативной базе для НФО (4937-У, 5075-У, 5084-У, 32-ФЗ)
Изменения в нормативной базе для НФО (4937-У, 5075-У, 5084-У, 32-ФЗ) Проектирование и оптимизация качества буровых растворов
Проектирование и оптимизация качества буровых растворов Презентация "Украшения" - скачать презентации по МХК
Презентация "Украшения" - скачать презентации по МХК St. Valentine’s Day
St. Valentine’s Day Турклуб "Сокол"
Турклуб "Сокол" Наурыз құтты болсын
Наурыз құтты болсын «Мировое хозяйство и международная торговля.»
«Мировое хозяйство и международная торговля.»