Содержание
- 2. УЧЕБНЫЕ ВОПРОСЫ: 1. Дискретные автоматы 2. Функциональные полные системы двоичных функций ЛИТЕРАТУРА: Основная Л1. А.К.Нарышкин «Цифровые
- 3. 1. Дискретные автоматы
- 4. Основные понятия и определения Обработка цифровой информации в ЭВМ производится электронными схемами—цифровыми устройствами (ЦУ), которые работают
- 5. Классификация 1. В зависимости от типа сигналов, и характера работы автомата во времени: - автоматы непрерывного
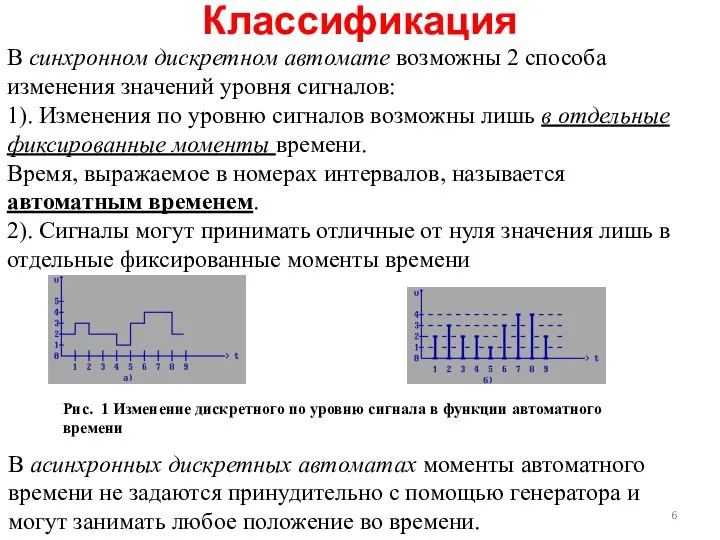
- 6. Классификация В синхронном дискретном автомате возможны 2 способа изменения значений уровня сигналов: 1). Изменения по уровню
- 7. 3. По зависимости сигналов на m выходах от сигналов на n входах. 1). Значения сигналов на
- 8. Основные понятия и определения Автоматы с кодированием значений сигналов цифрами (0 и 1) часто называют цифровыми
- 9. 2. Функциональные полные системы двоичных функций
- 10. Основные понятия и определения Алгебра логики оперирует следующими понятиями: 1). Переменная, которая может принимать два значения
- 11. Двоичные функции одного аргумента Известно, что от одного двоичного аргумента x может быть образовано четыре разных
- 12. Двоичные функции одного аргумента Функция y0 сохраняет нулевое значение. Это константа нуля (y0=0). Функция y3 -
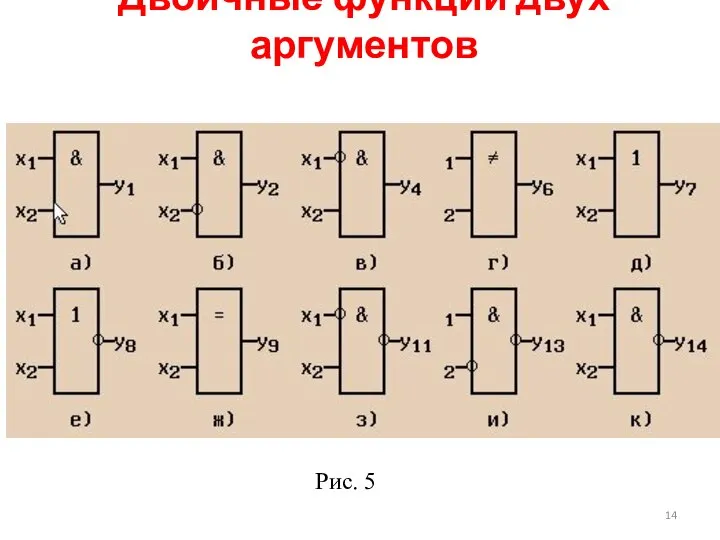
- 13. Двоичные функции двух аргументов От двух двоичных аргументов x1 и x2 могут быть образованы шестнадцать разных
- 14. Двоичные функции двух аргументов Рис. 5
- 15. Функциональные полные системы двоичных функций Подставляя в качестве аргументов одних двоичных функций другие двоичные функции, можно
- 16. Функциональные полные системы двоичных функций Функционально полная система функций, состоящая из трех функций - дизъюнкции, конъюнкции
- 18. Скачать презентацию













 Поведінка будівельних конструкцій під час пожежі
Поведінка будівельних конструкцій під час пожежі Двумерные массивы. Задачи
Двумерные массивы. Задачи Национальные костюмы народов России
Национальные костюмы народов России School Uniforms in different countries
School Uniforms in different countries Амнистия. Помилование.Судимость.
Амнистия. Помилование.Судимость. Параметры конструкции, Х-величины. Лекция 10
Параметры конструкции, Х-величины. Лекция 10 Использование видео и аудио в HTML
Использование видео и аудио в HTML Презентация по алгебре Тригонометрические уравнения и методы их решения
Презентация по алгебре Тригонометрические уравнения и методы их решения  Тире между подлежащим и сказуемым 5 класс - презентация_
Тире между подлежащим и сказуемым 5 класс - презентация_ Tajemnice Światła
Tajemnice Światła Базовые алгоритмы обработки одномерных массивов
Базовые алгоритмы обработки одномерных массивов ПРЕЗЕНТАЦИЯ НА ТЕМУ: «Витамины, гормоны, лекарства.»
ПРЕЗЕНТАЦИЯ НА ТЕМУ: «Витамины, гормоны, лекарства.» Основные принципы проектирования энергоэффективных зданий
Основные принципы проектирования энергоэффективных зданий Instructed second language vocabulary learning
Instructed second language vocabulary learning Кислородцентрированные соединения
Кислородцентрированные соединения  Водный и Огненный лабиринты
Водный и Огненный лабиринты Технология приготовления блюд обеда для туристов из Белоруссии
Технология приготовления блюд обеда для туристов из Белоруссии Контроллинг в системе управления
Контроллинг в системе управления Культура Японии
Культура Японии Благоустройство зоны отдыха для проведения массовых мероприятий с. Уточка» в Утянском сельском поселении
Благоустройство зоны отдыха для проведения массовых мероприятий с. Уточка» в Утянском сельском поселении Физическая форма
Физическая форма Нормативно-правовые основы формирования системы дополнительного образования в ДОО
Нормативно-правовые основы формирования системы дополнительного образования в ДОО Symbol of Mongolia
Symbol of Mongolia Государственные закупки. Строительство зданий
Государственные закупки. Строительство зданий Методические рекомендации по использованию технологии Эдварда де Боно «Шесть шляп мышления».
Методические рекомендации по использованию технологии Эдварда де Боно «Шесть шляп мышления». Пейзажи Беларуси
Пейзажи Беларуси Динамические структуры данных (язык Си)
Динамические структуры данных (язык Си) Многоэтажный жилой дом (КП)
Многоэтажный жилой дом (КП)