Содержание
- 2. 1.Базис(или база) Определение 1.1: Базис Базиcом векторного пространства V называтся упорядоченное множество линейно независимых (ненулевых) векторов,
- 3. Пример 1.2: есть базис для R2 1. B является ЛН : → → 2. Линейная оболочка
- 4. Определение 1.3: Стандартный / Естественный базис для Rn
- 5. Теорема 1.4: Для всякого векторного пространства, подмножество является базисом тогда и только тогда, когда каждый вектор
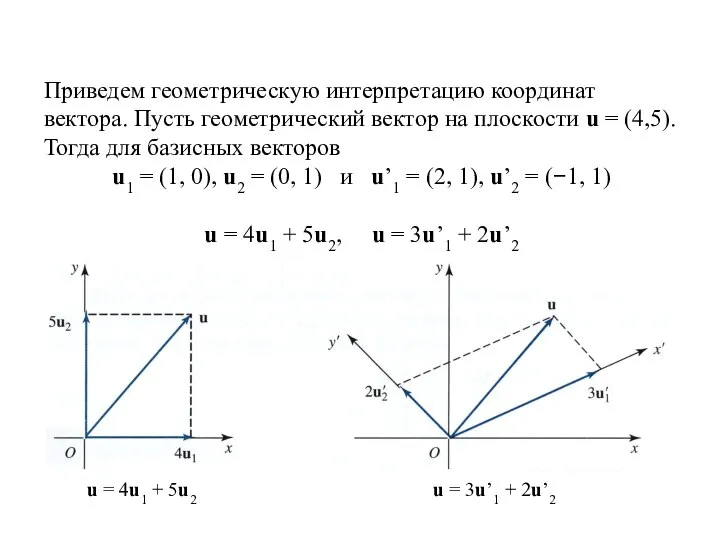
- 6. Приведем геометрическую интерпретацию координат вектора. Пусть геометрический вектор на плоскости u = (4,5). Тогда для базисных
- 7. Определение 1.5: Разложение по базису Пусть задан базис B = векторного пространства V ,тогда называют разложением
- 8. 2. Размерность Определение 2.1 Векторное пространство называется конечномерным, если оно имеет базу из конечного числа векторов.
- 9. Теорема 2.3: Для любого конечномерного пространства, все базисы имеют одинаковое число элементов. Доказательство: Пусть есть базис
- 10. Определение 2.4: Размерность Размерность векторного пространства есть число векторов в любом из его базисов. ( Обозначение
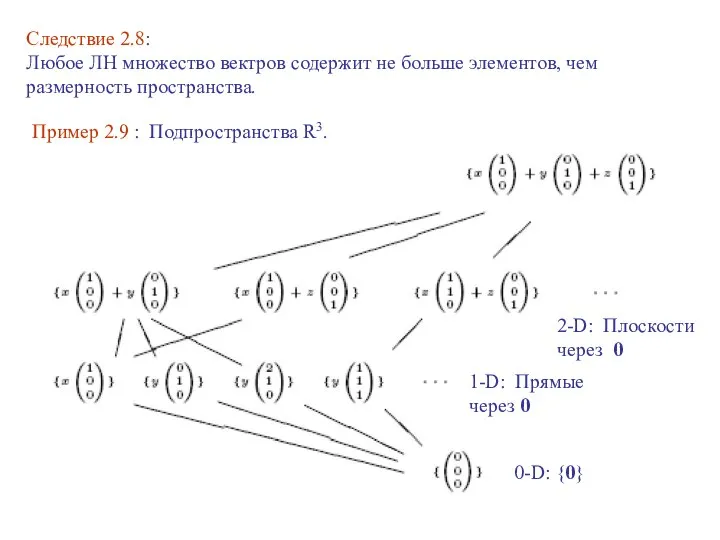
- 11. Следствие 2.8: Любое ЛН множество вектров содержит не больше элементов, чем размерность пространства. Пример 2.9 :
- 12. Следствие 2.10: Любое ЛН множество векторов может быть расширено до базиса. Следствие 2.11: Любой набор S,
- 13. 3. Матрица перехода от одного базиса к другому Пусть даны два базиса В = и G
- 15. Доказательство. Пусть Р – матрица перехода от базиса В к базису G: Точно также можно найти
- 17. Скачать презентацию

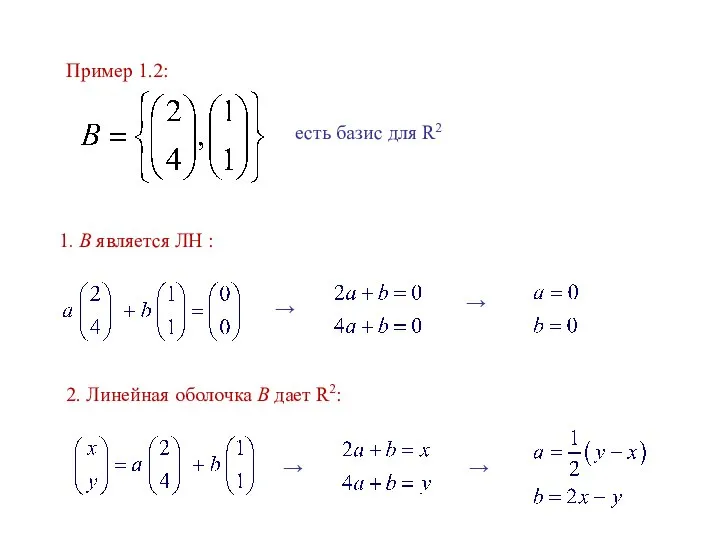










 Файл это : именованная область памяти на внешнем носителе
Файл это : именованная область памяти на внешнем носителе Первичный рынок ценных бумаг
Первичный рынок ценных бумаг  Sistemul serviciilor publice din economia naţională. (Capitolul 2)
Sistemul serviciilor publice din economia naţională. (Capitolul 2) Варианты размещения источника света в фотосъёмке
Варианты размещения источника света в фотосъёмке Хохломская роспись
Хохломская роспись Физиология крови
Физиология крови Комбинаторные задачи. Комбинаторика.
Комбинаторные задачи. Комбинаторика. 2. Product Planning & Development
2. Product Planning & Development Без названия
Без названия Юридические механизмы защиты прав человека в РФ
Юридические механизмы защиты прав человека в РФ 小 波 認 知 大 翻 翻 書
小 波 認 知 大 翻 翻 書 Система автоматического освещения рабочего пространства
Система автоматического освещения рабочего пространства Создание и деятельность корчемной стражи Подготовила студентка 2 курса экономического факультета группы Э092 Белешева Яна
Создание и деятельность корчемной стражи Подготовила студентка 2 курса экономического факультета группы Э092 Белешева Яна Organizatsia_sestrenskogo_ukhoda
Organizatsia_sestrenskogo_ukhoda Політичні партії, громадсько-політичні об’єднання та рухи
Політичні партії, громадсько-політичні об’єднання та рухи Презентация по МХК Художественная культура Арабского Востока Литература Арабского Востока
Презентация по МХК Художественная культура Арабского Востока Литература Арабского Востока  Droga krzyżowa
Droga krzyżowa Тема №9: Принятие управленческих решений
Тема №9: Принятие управленческих решений  Урок развития речи. Сочинение по картине Тутунова «Зима пришла.Детство.» Презентацию составила
Урок развития речи. Сочинение по картине Тутунова «Зима пришла.Детство.» Презентацию составила  Операторы ввода - вывода данных
Операторы ввода - вывода данных Технологии информационного моделирования на этапе строительства
Технологии информационного моделирования на этапе строительства Влияние физических упражнений на организм
Влияние физических упражнений на организм Функціональні системи вертольота Ми-2. Допоміжні системи
Функціональні системи вертольота Ми-2. Допоміжні системи Математика вокруг нас
Математика вокруг нас Основные идеи JSP
Основные идеи JSP ТРАНСПОРТ ГАЗОВ КРОВЬЮ
ТРАНСПОРТ ГАЗОВ КРОВЬЮ Презентация "Дали Сальвадор" - скачать презентации по МХК
Презентация "Дали Сальвадор" - скачать презентации по МХК Баженовское месторождение. Разработка схемы получения классифицированного щебня фракции -40+20
Баженовское месторождение. Разработка схемы получения классифицированного щебня фракции -40+20